人工分子磁体中的温差电效应
2018-12-12孙祝牛鹏斌
孙祝,牛鹏斌
(山西大同大学 物理系,山西 大同 037009)
0 引言
塞贝克效应是指温差产生电压、电流的现象。人们发现在半导体和金属中都可以实现塞贝克效应。随着纳米科学的进步以及器件的小型化,器件产生的热量成了越来越突出的问题,而且塞贝克效应可以直接把热能转换为电能,为清洁能源的产生提供了一个关键途径。近来,人们开始研究量子体系中的塞贝克效应[1-6],且其已成为一个新近研究热点,例如,在分子隧穿结中的塞贝克效应[1],外加铁磁电极产生磁致塞贝克效应[3],可以用于制作热传感器[4],也可以用温差产生自旋流[5]。
作为一类特殊的磁性分子,分子磁体[7-10]由于其特殊的大自旋及双稳特性,可产生自旋塞贝克效应[7-9]和较高的热电转换效率[10]。另外,人们已在理论和实验上实现了分子磁体的人工对应物,称为人工分子磁体[11-14]。人工分子磁体相对于分子磁体有一些优点,因为其是人工合成,制备和实验调控更方便,可用电学或磁学方法改变其大自旋所处势阱等参数,进而调控其热电特性。
鉴于这些研究进展,本文讨论人工分子磁体连接金属电极的塞贝克效应,研究人工分子磁体两端的温差导致的电流效应。结果表明,人工分子磁体中可以产生温差电流,且其铁磁态和反铁磁态对电流有很大影响,会产生位于费米面上方的正向电流和位于费米面下方的反向电流。铁磁态和反铁磁态的竞争以及反铁磁态内部的竞争导致正向电流和反向电流的叠加或抵消,进而产生非线性电流效应。温差电流随分子轨道能级变化展现出台阶现象。塞贝克系数在双通道时表现为反对称结构。
1 模型和理论方法

(1)
这里ε0描述分子轨道能级,U描述轨道电子双占据时的库伦排斥能。sz,±为电子自旋算符,Sz,±为大自旋算符,二者之间的耦合是各向异性的,用γ描述。为了简化问题,本文讨论一种特殊情形,γ=0且库伦作用U→∞(即只允许电子单占据)。相应的本征态和本征值为:HASMM|λ,m〉=Eλm|λ,m〉,其中λ=0,↑,↓,m∈[-S,S],S为大自旋角量子数,E0m=0,Eσm=ε0+δσJm/2,这里当σ=↑(↓)时δσ=1(-1).
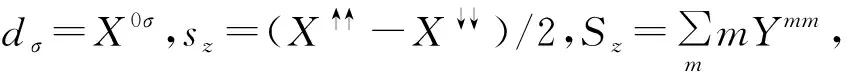
(2)

(3)
同时,为了计算电流[17-18],我们采用格林函数方法,相应电流公式为
(4)
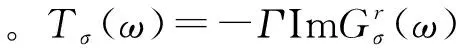
(5)
其中δσ=±1(σ=↑,↓),统计平均值P0m=
(6)

(7)
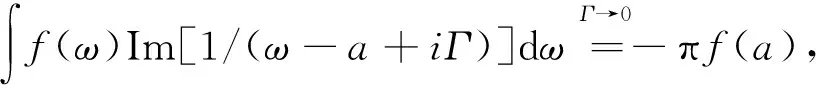
(8)
此式是下文数值讨论的主要出发点。同时,为了讨论人工分子磁体的温差电效应特性,给出塞贝克系数[21]
(9)
2 结果讨论
在数值讨论中我们取右电极参考温度为TR=0.01 K,左电极TL=θ+TR。人工分子磁体的自旋分别取S=1/2和S=3/2.

Fig.1 (a)-(c) Probabilities of states and (d) current as a function of temperature difference for various molecule energy levels for S=1/2图1 分子磁体自旋S=1/2时(a)-(c)不同能级位置下的态占据率以及(d)电流随温差的变化图
我们首先讨论S=1/2情形。图1给出人工分子磁体本征态的占据概率和电流随温差θ的变化图。参数为J=1.2,ε0=-1,0,1。S=1/2时人工分子磁体的单占据本征态为反铁磁态|↑,-1/2〉(|↓,1/2〉与其简并)和铁磁态|↑,1/2〉(及其简并态|↓,-1/2〉)。图1(a)中,当ε0=-1,所有的铁磁和反铁磁通道(指单占据本征能量与空占据本征能量之差)都在费米面(E=0)下方;当θ=0,即左右电极无温差,从图中可观察到P|0,±1/2〉=0,P|↑,1/2〉=0,P|↑,-1/2〉=0.5,这是因为电极两端无温差进而无电流,人工分子磁体中单占据一个电子在低能态(反铁磁态)。随着左电极温度升高,左电极部分电子被激发到费米面之上,留下空穴,右电极电子通过分子磁体流动到左电极,产生一个费米面下方的反向电流(方向从右到左),见图1(d)中ε0=-1曲线。同时可以观察到在温差较大时,铁磁态和反铁磁态都参与到输运中,且对电流的贡献一样大。同理,当ε0=1时,所有通道都在费米面之上,随着温差增大,激发电子可以通过通道产生从左到右的正向电流,见图1(d)中ε0=1曲线。当ε0=0时,铁磁通道和反铁磁通道关于费米面对称分布,铁磁通道在费米面上方,反铁磁通道在费米面下方。在图1(c)中观察到随着温度的增大,两个通道都参与到输运中,但占据率不同,反铁磁通道占据率明显高于铁磁通道。这说明此时既有正向电流,也有反向电流,二者有一部分相互抵消,所以图1(d)中ε0=0对应电流较小,且是负电流。这个结果明显不同于通常量子点[17],ε0和ε0+U两个通道关于费米面对称时产生的正向电流、反向电流相互抵消,电流为0。图1中通道之间竞争产生的正向电流、反向电流的叠加效应是非线性的,此特点从概率图和电流图中可看出,可见铁磁通道竞争力小于反铁磁通道,因为电子输运中趋向于处于低能态。

Fig.2 Current as a function of temperature differencefor various molecule energy levels for S=3/2图2 分子磁体自旋S=3/2时不同ε0下电流随温差变化图
为了进一步验证通道之间竞争导致的正向流、反向流叠加产生的非线性电流效应,我们讨论S=3/2情形,此时有两条反铁磁通道,|↑,-3/2〉和|↑,-1/2〉。从图1分析中我们预期这两条通道之间的竞争可导致非线性温差电流。图2给出了电流随温差θ的变化图,参数为J=1,讨论不同ε0对电流的影响。图2(a)中ε0=0,0.1,0.2时两条反铁磁通道都位于费米面下方,因为反铁磁通道竞争力远大于铁磁通道,此时产生的电流以反向电流为主。当ε0>0.3时,此时有一条反铁磁通道已位于费米面上方,可以观察到图2(a)中电流发生了明显突变,从负电流变成了正电流,并且ε0=0.3对应的电流曲线展现非线性效应。为了更仔细观察电流突变点附近行为,我们在图2(b)中给出0.2<ε0<0.3的变化图,可以看到ε0=0.255附近为电流突变点,即此点附近正向电流和反向电流持平,电流几乎为0。

Fig.3 (a)-(b) Probabilities of states and current for S=1/2, (c) current for S=3/2, and (d) Seebeck coefficient, as a function of molecule energy level图3 (a)-(b) S=1/2时态占据率和温差电流随分子轨道能级变化图,
以上讨论的是电流等物理量随温差的变化,接下来我们讨论给定温差的条件下,电流等物理量随分子轨道能级的变化。图3(a)-(c)讨论的是给定大温差的条件下态占据率和电流随轨道能级的变化图,而图3(d)给出的是小温差下塞贝克系数随随轨道能级的变化图。图3(a)、(b)中的参数为S=1/2,θ=20,J=1.2,观察到图1、2中在温差很大时态占据率和电流变化趋于稳定,所以此处分析大温差下电流随轨道能级的变化。在S=1/2时有两条通道参与输运(铁磁通道ε0+J/4和反铁磁通道ε0-J/4),当它们都在费米面下方时(ε0<-0.3),铁磁通道和反铁磁通道同时贡献反向电流,且态占据率相等,见3(a)-(b)中ε0<-0.3区域,这正是大温差下的特点,大温差抹平了费米面下方铁磁和反铁磁通道之间的概率不平衡。在-0.3<ε0<0.3区域,两通道都参与输运,但大温差下费米面下方电子数量仍大于费米面上方,所以反铁磁通道贡献的反向电流幅度大于铁磁通道贡献的正向电流,电流仍为负,此结论同样可从3(a)-(b)中读出。在ε0>0.3区域,分析和ε0<-0.3区域类似,此时温差电流为正向。在S=3/2时可以预期温差电流仍会出现台阶现象,同时台阶数量会增多。图3(c)中的参数为θ=20,J=4,此时参与输运的通道有四条,故而随着轨道能级变化出现四个台阶。图3(d)给出塞贝克系数随分子轨道能级变化图,参数为S=1/2时J=2和S=3/2时J=4,(d)图中右侧和上方坐标轴对应S=1/2。观察到S=1/2时塞贝克系数是线性的,S=3/2是反对称的,这是因为在线性响应区S=1/2时只有一条通道参与输运(反铁磁通道),而S=3/2时有两条通道参与输运(仍为两条反铁磁通道)。这个结果与量子点模型一致,当U=∞时只有一条通道(ε0)参与输运,塞贝克系数是线性的;当U有限时,两条通道(ε0和ε0+U)都参与输运,塞贝克系数是反对称的。这种反对称仍然源于正向、反向电流的竞争。
3 结论
本文讨论了人工分子磁体连接金属电极的塞贝克效应,发现人工分子磁体中可以产生温差电流,且其铁磁态和反铁磁态对电流有很大影响,会产生位于费米面上方的正向电流和位于费米面下方的反向电流。铁磁态和反铁磁态的竞争以及反铁磁态内部的竞争导致正向电流和反向电流叠加或抵消,进而产生非线性电流效应。温差电流随分子轨道能级变化展现出台阶现象。塞贝克系数在双通道时表现为反对称结构。这些结果源于正向、反向电流的竞争。
