量子点输运系统中电子的等待时间分布
2018-12-12王敏张超聂一行
王敏,张超,聂一行
(山西大学 理论物理研究所,山西 太原 030006)
0 引言
量子输运涉及纳米级导体中平均电流和散粒噪声的测量,在传统的研究中,电荷涨落往往是在一个长的时间周期内被研究,从平均电流中无法获得电子的短时行为。随着量子电子学的迅速发展[1-4],探测单电子在纳米结构中的相干转移成为人们关注的重点。于是,除了平均电流和散粒噪声外,高阶关联函数倍受关注[5-6]。理论上,利用电荷输运的全计数统计(FCS),人们可以计算电荷转移的高阶累积矩[7-8],而且,在介观结构中电荷转移的高阶关联函数已经在计数实验中被测量[9-12]。一般的输运电荷分布是在比连续转移两个电荷之间的时间间隔长得多的时间尺度上考虑的,丢失了许多短时物理信息。在量子输运过程中,电子实际上经历的是一种量子相干过程, 类比量子光学领域中光子等待时间分布定义,提出了电荷转移的等待时间分布概念[13-19]来描述介观结构中的短时物理性质。随着高频单电子发射和检测技术的迅速发展[20-21],等待时间分布成为刻画量子电子线路中单电子过程的有用概念[22]。Brandes提出采用马尔科夫主方程[23]方法来计算电子输运的等待时间分布,后来扩展到非马尔科夫机制[14,24-25],这些方法中可以考虑电子的相互作用,但与导线的耦合需要微扰处理。对于相干系统中的非相互作用电子,文献[26]提出用散射理论计算等待时间分布的量子理论,最近这种方法又被推广用于紧束缚模型[16]。本文考虑了量子点连接到左右导线的系统,导线用紧束缚链描述,基于散射理论和紧束缚模型我们研究了电子的等待时间分布,从而正确理解散射体的量子特征。
1 理论模型及哈密顿量
考虑一个单能级量子点连接到左右导线上,导线用紧束缚链描述,如图1所示。无相互作用的电子可以从左导线通过中间的量子点散射转移到右导线。对于研究电子的计数统计而言,可以不考虑电子的自旋,于是这个紧束缚模型的哈密顿量可以表示为
H=Hleads+Hdot+Htun,
(1)
其中Hleads表示导线的哈密顿量,
(2)

Fig.1 Schematic diagram of tight-binding model consisting of a quantum dot attached left and right leads图1 量子点连接到左右导线的紧束缚模型示意图
这里t为最近邻格点间的跃迁强度,Mα为α导线的格点数(α=L,R).量子点的哈密顿量Hdot可以表示为
Hdot=εd|D〉〈D|,
(3)
这里|D〉代表量子点中能量为εd的态。Htun表示量子点与左右导线之间的隧穿耦合项,它的形式为
Htun=-tL|ML,L〉〈D|-tR|1,R〉〈D|+H.c.,
(4)
这里tL表示左导线最右侧格点与量子点间的隧穿幅,tR表示量子点与右导线最左侧格点间的隧穿幅。系统的本征态由薛定谔方程H|φk〉=εk|φk〉决定,借助于格点紧束缚基{|l,α〉},系统的本征态|φk〉可以展开为如下形式:
(5)
由(5)式可以得到
(6)

(7)

(8)

(9)

(10)
把(9)和(10)式代入(6)、(7)、(8)式得到
(11)
由联立方程组(11)可以得到透射幅
(12)
2 等待时间分布计算
偏压V只加到左导线上,形成一个电子入射的能量窗口[0,eV](左右导线化学势都为零),电子通过此能量窗口可以从左导线入射通过量子点散射到右导线。一个电子通过右导线的某个确定位置后,到检测到下一个电子通过该位置时所经历的时间τ称为电子的等待时间。基于紧束缚模型和散射理论计算电子的等待时间需要引入散射态[16-17]:
(13)
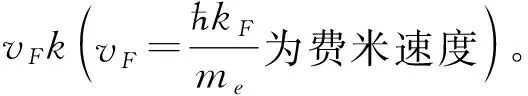
(14)
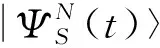
⊗…⊗ψN(t)],
(15)
这里Pn是置换算符。
在右导线中测量一个电子可以借助于单粒子投影算符来实现,电子在一个单粒子态的期望值就是检测到电子的概率。位于右导线x0处的电子探测器,在时间[t0,t0+τ]内,或者等效地在空间范围[x0,x0+vFτ]检测到电子的概率,可以用投影算符Qτ在单粒子态中的期望值来计算。于是算符1-Qτ在一个单粒子态中的期望值表示没有发现电子的概率。投影算符表示为如下形式

(16)
在时间间隔[t0,t0+τ]没有检测到电子的概率,称为空闲时间概率,用Π(t0,τ)表示,
Π(t0,τ)=Π(τ),
(17)
在稳态过程中与给定时刻t0无关。
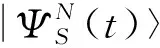
(18)
这个期望值可以简化为单粒子算符在单粒子态中的矩阵的行列式[16]
Π(τ)=det(1-Qτ),
(19)
其中Qτ是算符Qτ在单粒子态中的矩阵,矩阵元为[16,18-21]
(20)
其中
当N很大时,κ→0,计算(20)式中的积分时,把k和k′用上限代替即可,即
(21)
其中tκn=tk→κn。借助空闲时间概率Π(τ),等待时间概率分布可定义为ω(τ),表示为[16]
(22)

(23)
3 数值结果与讨论
3.1 偏压对等待时间分布的影响

(24)

(a)εd=0;(b)εd=0.4t;(c)εd=0.6 t;(d)εd=0.8 tFig.2 Waiting time distribution of single-channel quantum system under different bias Voltage.图2 单通道量子系统不同偏压下的等待时间分布
3.2 通道数对等待时间分布的影响
现在考虑具有两个相同且相互独立的输运通道,比如考虑电子自旋时,自旋向上和自旋向下的电子输运就是一种双通道输运。在两个独立通道情形下,左右导线仍保持为零温。

(25)

Fig.3 Waiting time distribution of single quantum dot system under different bias conditions in two-channel case图3 双通道条件下,单量子点系统的等待时间分布
对于具有两个相同且独立的双通道情形,在散射体右侧某个固定位置处可以同时检测到两个电子。对于自旋简并双通道,这并不违背泡利不相容原理。在数值计算中,取e=1,ћ=1,N=50,并且假定最近邻格点之间的跃迁强度为能量单位,即tL=tR=t=4 meV,vF=2t。图3给出偏压V=2t,单量子点能级分别取εd=0,-0.4t,-0.8t时的等待时间分布。显然独立通道的增加消除了短时等待时间分布的抑制效应,即τ=0附近的等待时间分布不再为零。从图中还可以发现,当量子点能级偏离费米能级时,短时等待时间分布函数整体上会被压低,而长时等待时间增加。实际上,当量子点能级偏离费米能级时,电子从左电极通过量子点能级散射到右电极是一种高阶过程,由不确定关系ΔtΔE≥ћ/2,在短时间内电子能量涨落可以很高。因此,即使量子点能级偏离费米能级,电子也有可能被散射到右电极,只是比直接隧穿散射的概率要小得多。
3.3 温度对等待时间分布的影响
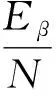
(26)

(27)
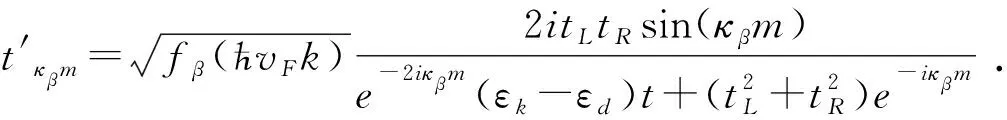
根据以上公式可以计算温度条件下的等待时间分布。图4(a)-(d)给出了单通道情况下,量子点能级分别为εd=0,0.3t,0.6t,0.9t时,几种不同温度下的等待时间分布。整体上看,随着温度降低(βmeV增加),等待时间分布的极大值向长时间方向移动,而且最大分布概率略有降低,但温度的影响主要是在最大分布概率附近,对长时概率分布影响较小。

(a)εd=0; (b) εd=0.3t; (c) εd=0.6t; (d)εd=0.9tFig.4 Waiting time distribution curves of single channel quantum systems at different temperatures图4 单通道量子系统在不同温度下等待时间分布曲线
此外,量子点能级离费米面越远,不仅等待时间分布变得更加平缓,长时等待概率增加,而且对最大分布概率的影响变大。最大分布概率随着温度的降低而降低,并在量子点能级远离费米面的情况下更为明显。这些等待时间分布的变化特性起源于电子服从泡利不相容原理和电子的不确定关系。
4 结论
本文分析了偏压、通道数以及温度对等待时间分布的影响。当量子点能级与电极费米面对齐,等待时间分布的峰值最高,且不依赖于偏压。当量子点能级偏离了费米面时,分布函数依赖于偏压。随着偏压增加,分布函数的峰值会增加,等待时间概率向短时方向移动。对于双通道量子点系统,零等待时间时等待时间分布不为零,而且随着量子点能级偏离费米面,零等待时间时等待时间分布概率降低。电极温度通过费米分布函数也会对等待时间分布产生影响,温度降低等待时间分布的极大值向长时间方向移动,且最大分布概率随着温度的降低而降低,并在量子点能级远离费米面的情况下更为明显。等待时间分布对于正确理解散射体的量子特征有很重要的意义。
