成人高校毕业生学位评审预测模型及其应用
2018-12-12支天云陈晓冬
支天云,陈晓冬
(1.山西大学 继续教育学院,山西 太原 030006;2.山西省农业科学院,山西 太原 030006)
0 引言
目前,成人高校毕业生学位与学历一样越来越受到重视。各成人高校对毕业生学位评审大都采用定性分析方法,实际操作中由于人为干预因素较多,例如评审人员专业基础薄弱、工作经验不足、学术能力欠缺导致主观判断不准备。如何准确、高效地对成人高校毕业生学位进行评审,是各成人高校面临的现实问题。与普通高校相比,成人高校毕业生的学位评审更为复杂,各个评审指标与学位获得之间是一种非线性关系,神经网络针对非线性问题有较强的映射能力,是处理这类问题的有力工具[1-2]。
BP网络[3-4]具有很强的容错、学习和纠错能力,由于存在局部最小点问题,无法保障能求出全局最小值,可能发生网络瘫痪。概率神经网络、灰度关联分析法需要对输入变量进行归一化。LVQ神经网络具有结构简单,容易收敛等特点,且不需要进行归一化和正交化,只需要计算输入变量与竞争层之间的距离[3],从而实现模式分类,简单易行。但是神经网络受拓扑结构和训练样本的影响,在有冗余属性时,训练时间长,且速度慢,不能对冗余属性进行约简。粗糙集(Rough Sets简称RS)理论[5-9]的关键技术是在保持系统分类能力不变的前提下,对冗余属性进行约简,减少网络的输入层矢量,缩小网络的空间维数,降低网络运行成本,对神经网络的快速训练是一个有效方法。
文献[2]采用LVQ神经网络对普通高校学位评审进行了分析。运用同样方法,对于情况比较复杂、评审指标较多的成人高校毕业生学位评审,预测精度和运行效率都比较低。本文基本思想是:选用某成人高校某专业的学位评审原始数据作为训练测试样本,将RS方法作为LVQ神经网络的前置系统,通过属性约简,减少评审系统的指标(属性)数量,再将RS处理后的信息作为LVQ神经网络输入变量,建立了一个基于RS-LVQ的成人高校毕业生学位评审预测模型,利用测试样本对模型进行测试,并与普通LVQ网络进行比较,结果表明,本文建立的网络模型稳定可靠、抗干扰能力强、训练速度快、预测精度高、具有较高的应用价值。
1 基于粗糙集(RS)-LVQ神经网络的评审预测模型
本文通过RS理论属性约简,对输入数据进行预处理,优化成人高校毕业生学位评审指标,并将优化指标对应的数据输入到LVQ神经网络进行训练,构建了基于RS-LVQ神经网络的成人高校毕业生学位评审预测模型,如图1所示:文章对RS和LVQ的相关原理作了简要介绍,更详细的阐述详见文献[3,10]。
1.1 基于RS理论方法的数据预处理
Z.Pawlak提出的RS[11]理论为研究不完整数据、提取有用特征、剔除冗余信息,提供了一个有用的工具,在保持分类能力不变的情况下对属性进行冗余属性约简是RS重要功能。利用RS方法得到的属性约简集输送到LVQ神经网络,作为输入层的训练数据,这样的数据表示清晰,网络的训练次数、训练时间得到减少,抗干扰能力增强,节省了模式识别费用,网络训练稳定性好。目前,常用的属性约简算法有[12]:基于正域的方法,基于差别矩阵方法,一般约简算法,基于正域的启发式算法,基于信息熵的互信息方法,二进制可辨矩阵变换算法[13]等。上面几种方法在约简功能上各有优劣,本文采用基于差别矩阵的属性约简算法[13-18]。

Fig.1 Evaluation forecasting model based on Rough Set and LVQ图1 基于RS-LVQ神经网络的评审预测模型
定义1:令P为一个等价关系,R⊂P,如果ind(P)=ind(P-{R}},则R为P中不必要的,否则R为P中必要的。设若Q是独立的,且ind(Q)=ind(P)则Q为P的一个约简。核[19]与约简关系如下:Core(P)=∩red(P),red(P)表示P的所有约简,Core(P) 为P的核。
求出所有约简是一个NP-hard问题,一般情况下并不需要得出所有约简,只要得到一个接近最优约简,即找到一个满足R∩kij≠ø 的最小属性集合R即可。
定义2:设S=(U,A,V,F)是一个决策信息系统,|U|=n,其中A=C∪D,C是条件属性,D是决策属性,V={va|a∈A},对任意xi,xj∈U,a∈C如果a(xi)≠a(xj) (其中xi≠xj),则属性a值的差别矩阵描述如下:
M(U,C)=(kij)n×n(i,j=1,2,…,n),
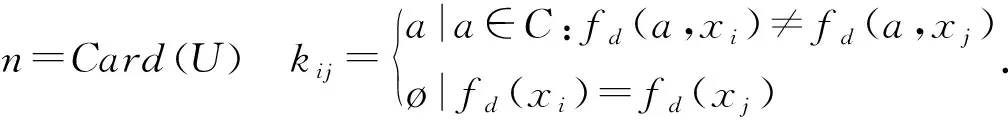
差别矩阵M(U,C)的差别函数记成:
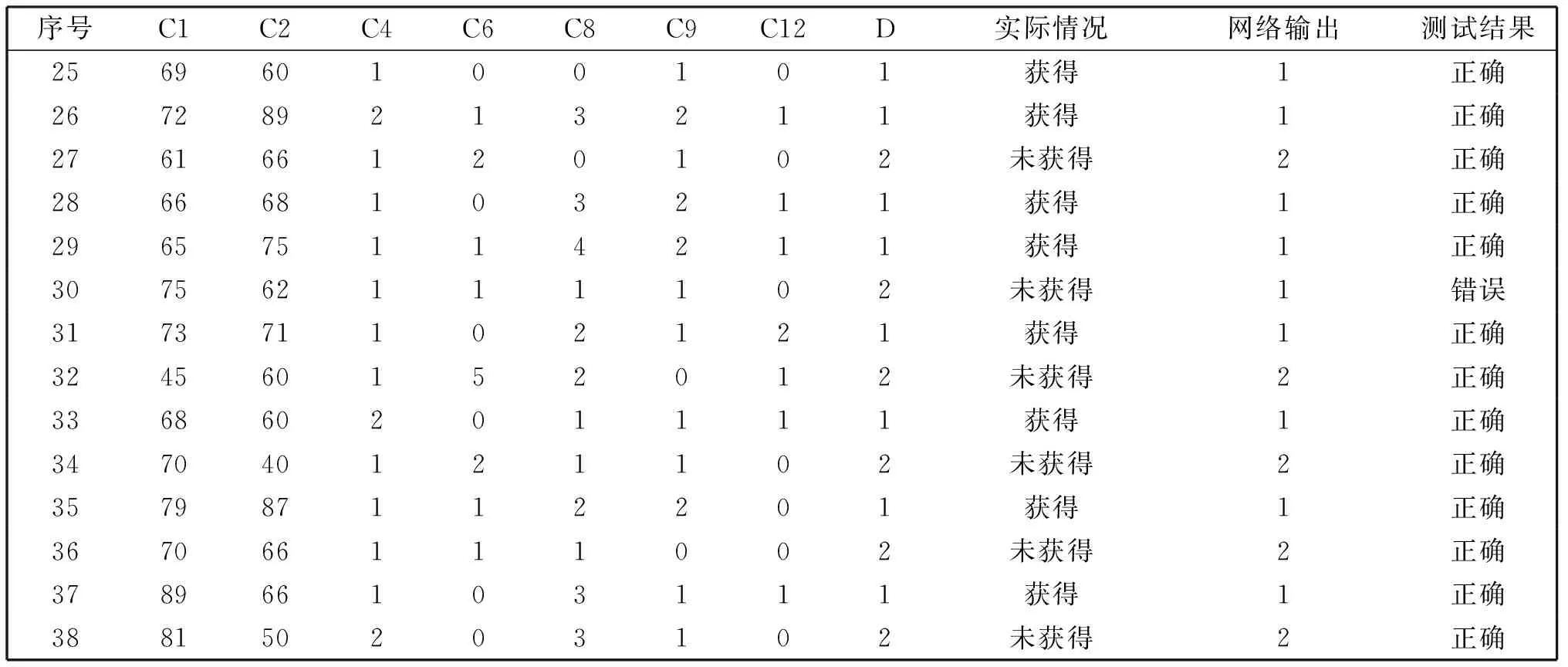
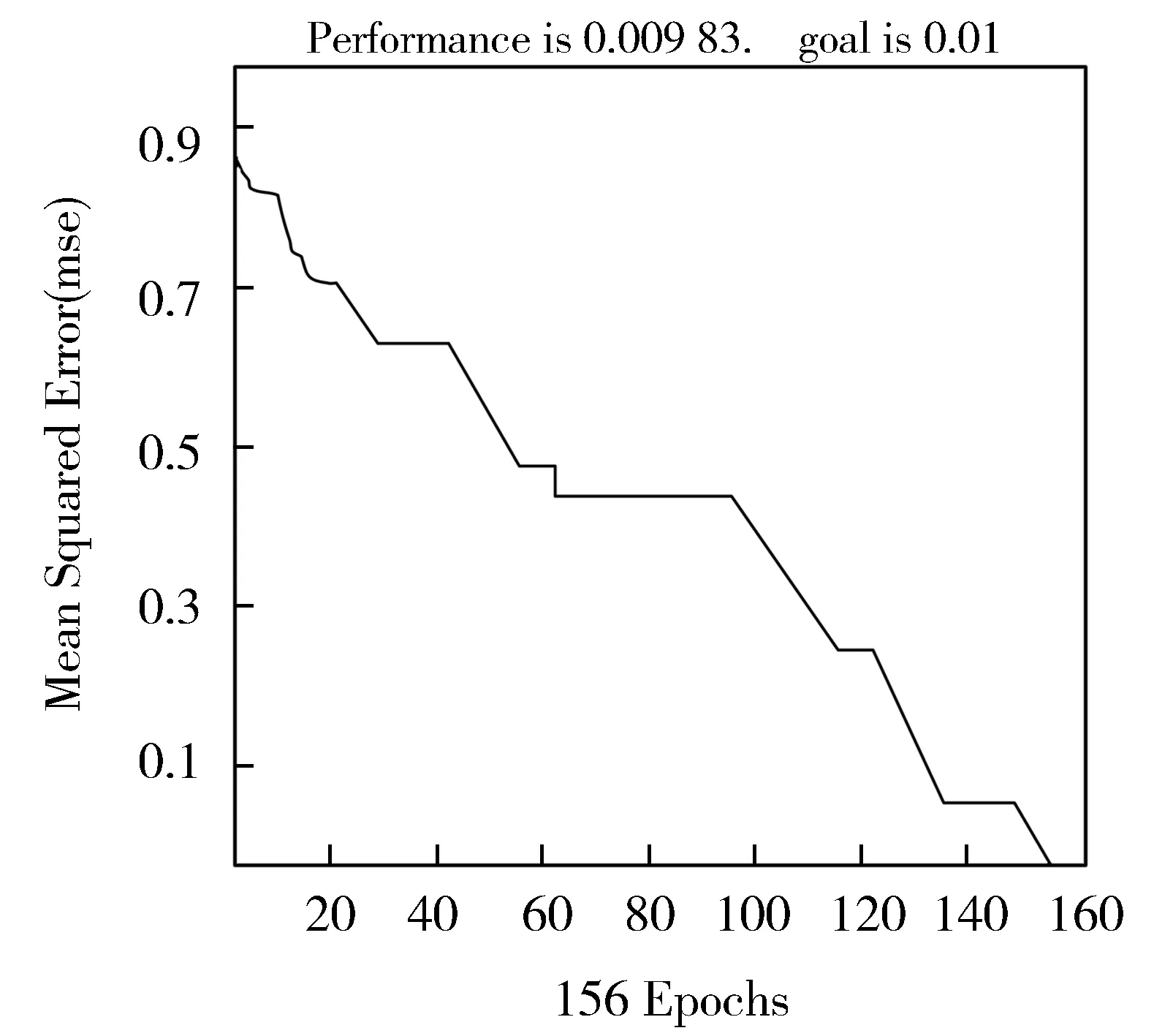
Fm(U,C)(a1,a2,…,an)=∧{∨(kij),1≦j 其中每一个合取范式∨(kij)构成一个约简,m为C中条件属性个数。 LVQ是学习矢量化神经网络的简称,属于竞争型神经网络,由输入层(Input layer)、隐含层(Hidden layer)和输出层(Output layer)组成,如图2所示。其基本原理是:给定初始权值Wi(0),利用训练样本对网络进行训练,并逐步调整神经元的权值,等训练若干次后网络神经元权值基本稳定于某固定值,网络收敛,此时即可输入待测样本进行测试。 Fig.2 LVQ neural network classifier图2 LVQ神经网络分类器 1.2.1 LVQ神经网络学习算法 (1)设置变量和参量:输入向量x(n)=[x1(n),x2(n),…,xN(n)]T; 权值向量Wi(n)=[wi1(n),wi2(n),…,wiN(n)]T,i=1,2,…,N.n,N分别为迭代次数和总次数; (2)初始化权值向量Wi(0)及学习速率η(0); (4)分类正确性判别。根据以下公式调整网络神经元的权值: ifHwc=Hxithen Wc(n+1)=Wc(n)+η(n)[X-Wc(n)] elseWc(n+1)=Wc(n)-η(n)[X-Wc(n)], 其中Hwc表示与获胜神经元相关联的类,Hxi表示与输入向量相关联的类,Hwc=Hxi表示分类正确,对其它神经元权值保持不变; (6)迭代次数判别: ifn≤Nthen go(4)elseend。 1.2.2 LVQ神经网络的训练 通过LVQ学习算法建好网络之后,采用Matlab 7.0[20]软件包对网络进行训练,测试和仿真命令如下: Net.trainParam.epochs=n;Net.trainParam.goal=e;Net=train(net,P,T) 其中P为网络的输入样本矢量;T为网络的期望输出;n为最大的训练步数;e为训练的要求精度。 1.2.3 LVQ神经网络的测试与仿真 对于训练好的LVQ神经网络,网络收敛于给定的预测精度,以后每输入一个测试样本向量P,就会产生相应的输出分类,命令设置为:Y=sim(net,P) 和Yc=vec2ind(Y)。 RS-LVQ神经网络模型的稳定性,在一定程度上取决于成人高校毕业生学位评审指标(简称:学位指标)的选择上。本文学位指标选取的思想:一是学位指标能正确地反映成人高校毕业生的真实现状;二是学位指标在不影响反映现实状况前提下进行适度筛选和优化,避免指标过多和信息交叉带来的建模困难,提高预测模型的时效性和准确度。在学位指标的选取上,为了全面反映成人高校毕业生学位评审现实状况,我们会选取尽量多的学位指标,但是这些指标之间可能存在线性关系,指标过多不仅影响模型的预测效果,而且可能造成网络系统瘫痪,因此,根据成人高校实际情况和专家经验,首先对学位指标进行初选。 成人高校与普通高校毕业生在入学成绩、学习能力、课程设置、毕业要求上的差异决定了其学位的评定标准、评定指标选择的不同。普通高校毕业生一般从课程、实践、论文、英语、计算机等级等五大方面成绩来综合评价毕业生学位的获得情况[2],而成人高校毕业生的实际情况要比普通高校复杂得多。综合考察多所成人高校毕业生的学位评定标准,我们主要从以下十二个指标方面进行评价:课程平均成绩C1、学位外语成绩C2、学位专业课成绩C3、社会实践成绩C4、学位论文成绩C5、考试舞弊次数C6、补考课程数C7、服务社会与科技活动C8、成人计算机水平考试C9、到课率C10、作品C11、论文发表C12。有些成人高校还把重修学分、学术交流、专利、考研、职业技能鉴定、演讲活动等作为评审指标。 C1、C2、C3三个指标是用分数表示的,分数越高越好;C4、C5是用等级来表示的,分为不合格、合格、优良三个等级,依次用0、1、2来表示;C6、C7、C8 指标用次数来衡量,C6、C7的次数越少越好,数值0表示没有舞弊和补考,C8指标也是以次数来衡量的,次数越多越好,没有参加者其值为0;C9指标分为三个等级,即没有报考或没有通过者其值为0,通过为1,优良为2;到课率分为9个等级,即0-10%用0表示,11%-20%用1表示,…,91%-100%用9表示;作品和论文发表分为3个等级,即发表一篇用1表示,二篇用2表示,三篇及以上用3表示;学位评审结果分为两种结果,即获得学位和未获得学位,获得学位者用“1”表示,未获得学位者用“2”表示。本文选取某成人高校某专业一个班级原始数据作为研究对象,删除各指标信息完全相同的重复行得到学位评审决策信息表,如表1所示,决策属性D=“学位评审情况”。 针对成人高校学位评审所建立的决策信息表,S=(U,A,V,F),U为不同学生的学位评审对象,|U|=38,A=B∪D,其中条件属性B={C1,C2,…,C12}为十二个评审指标集合,D={学位评审情况}表示学位评审情况。利用粗糙集工程软件ROSETTA来完成基于差别矩阵的属性约简算法,共得到决策信息表的二个最小属性约简{C1,C2,C4,C6,C8,C9,C12}和{C2,C4,C5,C6,C8,C9,C12}, {C2,C4,C6,C8,C9,C12}为核。 本文采用表1样本集的前24个学生学位指标相应数据作为RS-LVQ网络模型的训练样本,其余14个学生数据作为测试样本。假设首先选取与最小约简B1={C1,C2,C4,C6,C8,C9,C12}相对应的表1数据作 表1 原始指标数据 为训练样本。B1指标集元素个数7作为LVQ网络输入层神经元数目,经过多次试验选择14作为隐含层神经元数目,输出层神经元数目为2,表示某个学生获得学位还是没有获得学位,获得为“1”,没有获得为“2”,所以LVQ神经网络结构为7×14×2。实验采用表1原始数据和Matlab 7.0软件编程环境,根据前述LVQ神经网络学习算法,网络建立的具体命令设置如下:P=[7×24矩阵]T;%表1中24组数据构成7×24矩阵,输入变量取其转置C=[2 2 1 1 2 1 1 2 2 2 1 2 1 2 2 1 1 2 1 1 2 1 2 1],类别输出,“1”表示获得学位,“2”表示没有获得学位。 T=ind2vec(C),将C转为目标向量; Net=newlvq(minmax(P),14,[0.5,0.5]);%[0.5,0.5]表示50%属于第1类,50%为第2类, 学习速率、学习函数均采用默认值,分别为0.01和learnlv1[3]; Net.trainParam.epochs=1 000,最大训练步数为1 000; Net.trainParam.goal=0.01,网络训练精度为0.01; Net=train(net.P.T),网络训练; Yc=sim(Net,P),网络训练结束,仿真输出; Y=vec2ind(Yc),网络输出转化为类别向量。 经过训练,当训练步数达到135步时,网络能基本平滑收敛于全局最小值,误差达到要求,训练过程如图 3所示。说明模型能正确区分样本的类别,结果十分理想,训练样本能正确地分类为“1”(获得)或“2”(未获得),与实际情况完全符合。 Fig.3 LVQ Training error curve when minimum attribute sets B1图3 最小属性约简B1的LVQ训练误差曲线 为了检验RS-LVQ神经网络模型的预测精度,现将测试样本逐一输入到模型中进行测试,在经过MATLAB 7处理之后得到测试结果,如表2所示。 表2 测试样本输出结果 前面利用RS方法选择的最小属性约简集B1相应的训练样本作为网络的输入变量,训练得到了RS-LVQ网络预测模型,现将另一个最小属性约简集B2 相应24个学生的训练样本集逐一输入RS-LVQ网络进行训练学习。通过不断地实验发现,将隐含层设置为14个神经元数目时可以最大限度地提高预测精度,经过156步训练,误差达到了0.01,训练结果如图4所示。比较图3和图4可知,无论从训练步数还是达到目标误差速度上,图3性能都要比图4优越,所以最终选择图3作为成人高校毕业生学位评审预测模型,亦即选择B1对应的训练样本作为RS-LVQ网络预测模型的LVQ的输入数据,对网络进行训练学习。 为了比较基于粗糙集理论的属性约简对LVQ神经网络学习效率的影响,本文同时将未约简的全部十二个评审指标B={C1,C2,C3,C4,C5,C6,C7,C8,C9,C10,C11,C12}相应原始数据输入到LVQ神经网络,经过多次试验,选取25作为隐含层神经元数目对网络进行训练,其余参数与最小约简集B1={C1,C2,C4,C6,C8,C9,C12} 训练样本一样,网络训练结果如图5所示。 Fig.4 LVQ Training error curve when minimum attribute sets B2图4 最小属性约简B2的LVQ训练误差曲线 Fig.5 LVQ training error curve of all attribute sets B图5 全部属性集B的LVQ训练误差曲线 说明采用全部属性训练样本需要785步才能达到目标误差,而最小约简训练样本只需要135步即可到达,如图3所示。假如调整目标误差为0.001,最大训练步数为10 000,最小约简训练样本经过550步达到目标误差,而全体属性集训练样本需要经过5 492步才达到。有时训练步数超过10 000步也达不到目标误差,可能是遇到了“死”节点问题。说明使用全部属性集训练样本训练网络不能满足要求,运用RS方法进行属性约简是必要的。 将测试样本分别输入RS-LVQ网络预测模型与LVQ网络进行比较,实验结果如表3所示。表3说明,本文构建的RS-LVQ神经网络学位评审预测模型,简化了LVQ网络的结构,输入矢量减少了42%,运行效率提高了75%,准确识别率提高了14.4%。 表3 RS-LVQ网络预测模型与LVQ网络比较 本文采用某成人高校毕业生的学位评审原始数据作为训练样本建立了RS-LVQ神经网络学位评审预测模型,并进行了实证分析,结果表明: (1)利用粗糙集理论方法对成人高校毕业生的学位评价指标进行筛选,在不损失信息的前提下得到两个最小属性约简数目均为七的评价指标:{C1,C2,C4,C6,C8,C9,C12}和{C2,C4,C5,C6,C8,C9,C12},将其对应的训练样本分别输入至RS-LVQ网络模型,比较其训练结果,最终择优选择{C1,C2,C4,C6,C8,C9,C12}对应的训练样本作为本文构建模型RS-LVQ的输入矢量。 (2)最小属性约简,不仅简化了网络结构,提高了学习效率,而且网络模型的分类能力不会改变。而将全部属性评价指标的学习样本输入模型,经过785步,网络才能收敛于目标误差。当调整目标误差为0.001,最大训练步数为10 000时,网络经过5 492步才能达到训练精度,有时超过10 000甚至更多步也不能收敛,说明采用全部学位评价指标的原始数据训练网络不能收到满意效果。 (3)RS-LVQ网络预测模型与LVQ网络进行比较,结果表明:RS-LVQ网络预测模型在分类预测精度和学习效率上均优于LVQ网络。 (4)RS-LVQ网络学位评审预测模型,避免了人为因素影响,评判结果客观可信,有些评价指标如计算机等级考试等没有具体成绩,只能按等级区分,如果有具体分数,就可使学生间数据有更高的可比性,效果会更好。 成人高校情况较为复杂,生源来自社会,不同年级相同专业、同一年级不同专业的学生人数相差较大,每班超过20或30人的很少,且有三分之一甚至更多学生因各种原因中途退学或不能毕业,因此作者参考了大量成人毕业生数据,从中筛选出具有代表性的某专业某班毕业生42人,合并5人相同信息后得到38人作为本文研究数据。随着研究的深入,我们还将广泛联系同类高校,采集更多的真实数据样本做进一步的研究。 粗糙集理论与LVQ神经网络的相结合,在成人高校毕业生学位评审预测应用方面尚不多见,本文进行了初步的尝试与探索,效果良好,为成人高校毕业生学位评审工作提供了新的思路与方法。实验中,我们还将RS-LVQ学位评审预测模型与BP神经网络[3-4]进行了比较研究,限于篇幅,不再赘述。1.2 LVQ神经网络分类器

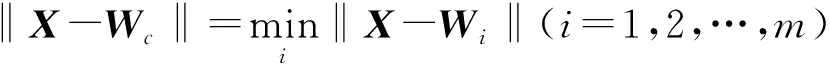
2 实证分析
2.1 成人高校毕业生学位评审指标的选取
2.2 粗糙集数据的预处理(Data of Rough Set preprocessing)
2.3 LVQ神经网络的建立、训练与测试
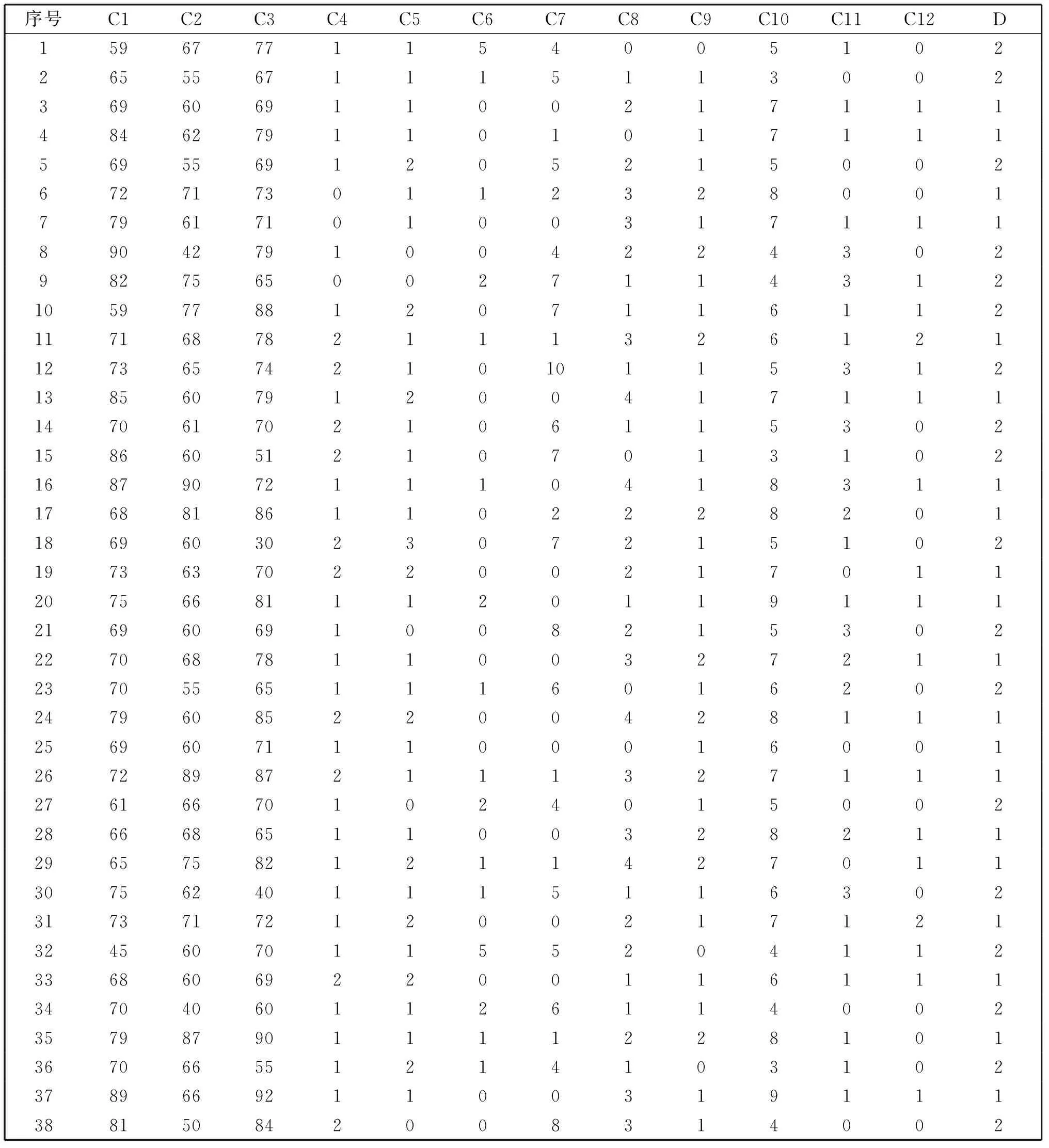

2.4 两个最小属性约简B1={C1,C2,C4,C6,C8,C9,C12}和B2={C2,C4,C5,C6,C8,C9,C12}在构建RS-LVQ神经网络模型中的择优选择
2.5 粗糙集数据约简前后的RS-LVQ网络仿真对比

2.6 RS-LVQ网络预测模型与LVQ网络在测试样本上的比较

3 结论
