数学建模在高中数学教学中的融入

江苏省南通大学附属中学 李带兵

在高中教育阶段，数学属于一门必修课程，教学目标是把课本知识和现实问题融为一体，最终解决实际问题。在高中数学课程教学中融入建模思想是新课改发展的必然，教师应该结合一些简单的现实问题进行适当假设，构建数学知识能解决这一生活问题的数学模型，指导学生据此解决实际问题，这对提升他们应用数学知识解决实际问题的能力有着积极意义。

一、解析数学建模案例，培养学生建模意识

要想在高中数学教学中有效融入建模策略，教师首先需要选取适当的建模案例进行示范与解析，让学生在现实问题情境中充分体验到数学建模的具体应用，逐步培养他们的数学建模意识。因此，高中数学教师在选择建模案例时，要选择涵盖丰富的实际问题，揭示建模策略的具体应用，将现实问题抽象成数学模型，增强彼此之间的联系，吸引学生主动建模。

以“指数函数”教学为例，教师播放现实中细胞分裂和铀核裂变两个视频，抽象出两个建模案例：一种细胞在进行分裂时，由1个变成2个，2个再变成4个，4个变成8个……进行x次分裂，分裂次数x和细胞个数y之间的函数解析式为y＝2x（x∈N＊）。铀核裂变可以产生相当大的能量，其在裂变反应中1个铀核被1个中子击打，该铀核可以释放出3个中子，这3个中子又分别击中3个铀核，将会释放出9个中子……中子对铀核进行x次击中后，击中铀核次数x同释放出中子数量y之间的函数解析式是y＝3x（x∈N＊）。搭配问题：y＝2x与y＝3x这类函数的解析式有什么共同特征？学生在讨论中回答：函数解析式都是指数形式，底数为定值且自变量在指数位置，引领他们建立指数函数模型，了解指数函数的概念，为后续学习做铺垫。

如此，利用现实案例解析如何建立数学模型，关键在于找准现实生活与数学模型之间关联，以此为切入点进行深入思考，这是学习数学建模的开始，使学生养成良好的建模意识。

二、选择恰当生活素材，指导学生建立模型

在高中数学课程教学中融入数学建模，离不开大量生活素材的辅助，这是建立数学模型的根本出发点，既能够强化数学教学与实际生活之间的关系，还能够焕发学生的学习兴趣与热情。所以，高中数学教师建模教学中，应当选择恰当的生活化素材，从学生熟悉的日常生活着手，指导他们在生活化课堂上尝试建立数学模式，有助于对数学知识的理解和掌握。

在展开“任意角的三角函数”教学时，教师先带领学生复习任意角的概念，思考任意角和之前学习角的概念有什么区别？目的是为学习任意角的概念做准备。并利用生活素材创设情境引出主题，如下图所示：假如一个摩天轮的中心和地面之间的距离是h0，其直径长度是2r，在转动时作匀速运动，每圈需要6分钟，假如你坐在摩天轮的点A位置，逆时针从该位置出发，那么时间t和距中心地面近距离h之间的函数关系式是？

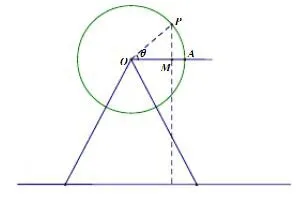
之后，师生一起分析在整个运动过程中，高度h是如何变化的？在讨论中得出结论：刚开始时h逐渐变大，当升至最高点后逐渐变小至最低点，然后再逐渐变大，直至回到出发点；第二周，第三周……周而复始，呈现周期现象。提问：该用什么样的函数模型刻画这种运动？先从特殊情形入手，如：20s后，人距离地面的高度是多少？回答：h＝h0＋rsin20°，且解释式子。

上述案例，教师结合实际问题恰当导出任意角三角函数的概念，显现出三角函数的概念的周期性特征，促使学生积极参与到思考和探索活动中，指导他们构建相应的数学模型。

三、传授数学建模方法，提高学生建模水平

在高中数学教学过程中为更好地融入建模思想，传授数学建模方法是关键，当呈现出生活案例后，教师需指导学生先准确分析题目，在整体上把握题意，理清案例中的复杂关系，挖掘蕴含的深层次关系，把握好问题的深层结构。同时，高中数学教师应要求学生充分利用案例中的已知信息，克服思维定式，在发散性思维中建立数学模型，并学会举一反三。

在“空间几何体的结构”教学中，教师在多媒体课件中展示一些世界上经典建筑物，包括华表、悉尼歌剧院、伦敦大本钟、水立方、金字塔等，提出问题：不少建筑物能够给人带来美的享受，大家知道是什么原因吗？借此导出空间几何体这一新概念。追问：这些建筑物由哪些几何体组合而成的？呈现一些立体图形，包括球体、棱台、棱锥和柱子等，设计问题：大家可以按照具体标准将它们分成不同类别吗？引导学生结合实物总结多面体及多面体的面、棱、顶点的定义，并展示棱柱图片，要求他们将生活中的实物与图片进行对比，找准棱和顶点，分析面与面之间的关系，使其自由讨论，总结棱柱的主要结构特征：顶面和底面是相互平行的，剩余各个侧面均为四边形，而且各组相邻四边形的共用边也相互平行，以此构建出数学模型。

在上述案例中，教师引领学生逐步建立数学模型，找准实物和数学图形之间的关系，以及各个部位的对应关系，帮助他们掌握一定的数学建模方法和技巧，提升数学学习效率。

总之，在高中数学教学活动中融入数学建模，既是新课改的主推方向，也是提高教学质量的有效途径，教师在日常教学中需引入恰当的建模案例和生活素材，指导学生掌握建立数学模型的方法与技巧，进而产生最佳教学效果。