转化策略在解题中的应用

山东省寿光现代中学 刘振宇

化归与转化的思想是解决数学问题的根本思想，解题的过程实际上就是一步步转化的过程。数学中的转化比比皆是，如未知向已知转化，复杂问题向简单问题转化，新知识向旧知识的转化，命题之间的转化，数与形的转化，空间向平面的转化，高维向低维转化，多元向一元转化，高次向低次转化，超越式向代数式的转化，函数与方程的转化等，都是转化思想的体现。善于观察、善于联想是进行解题转化的前提，本文通过介绍解题转化的几个基本策略以达到指导解题的作用。

策略一：根据函数结构特点转化为函数性质问题

A.7 B.8 C.9 D.10

【评注】本题通过参数的分离将原函数分离为两个函数的和，分析两个函数的性质以及函数存在最值的条件得出参数b=0，且为奇函数，最大值与最小值和为0，故有a=3，结果可得。

策略二：二元函数转化为一元函数

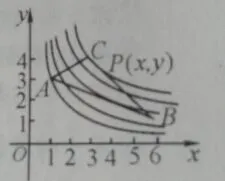
【评注】此题所求为二元最值问题，其约束条件是不等式，所以无法通过约束条件将目标函数转化为一元函数，转而从目标函数本身出发，通过令k=xy，引入参数k，获取含有x，y的等式，利用此等式，将二元函数转化为一元函数然后利用k在一元函数中的几何意义，数形结合，找到了取得最大值的条件。

策略三：多元变量向一元变量的转化

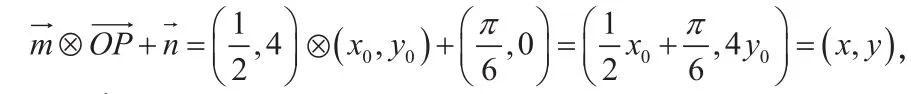
【评注】将题目中的元素统一，条件和结论统一，是一种重要的思维方式，它体现了转化过程中的和谐与统一。

策略四：把握新信息，新命题与传统知识的转化

【评注】本题通过一个新的运算形式考查集合的运算问题，要解析此信息，就必须了解集合M,N之间的关系，通过对条件a+b=c+d，ab＜cd＜0的分析，该问题转化传统的不等式性质的应用问题，由此可确定两集合关系，从而得解。

转化与化归是解题常用方法，对于任何一道数学题，都包含一定的数学条件和关系。要想解决它，就必须依据题目的具体特征，对题目进行深入的、细致的、透彻的观察，然后认真思考，透过表面现象看其本质，这样才能正确转化解题思路，找到解题方法。