交流-直流转换器高转换效率控制方法
2018-12-07罗小青何尚平
罗小青,陈 艳,胡 荣,何尚平
(南昌大学 科学技术学院,江西 南昌 330029)
由于反激式交流-直流(Alternating Current/Direct Current,AC/DC)变换器具有结构简洁、可靠性好、宽输入范围及多路输出等优点,因而在消费电子中得到广泛运用[1-8].然而,在电能存储和转移的过程中,由于转换效率较低导致大部分电能以热能的形式被耗散而没有被加以利用,进而导致开关电源系统温度升高甚至会引起灾难性事件的发生,因此研究影响功耗的各个系统参数具有重要意义.笔者提出一种基于状态空间平均法的反激式交流-直流变换器的功率级模型,并基于该模型进行MATLAB分析,得出了影响交流-直流系统功耗的各参数变化曲线,从而提出了一种优化的恒压控制策略.通过实测验证,应用该控制策略的交流-直流变换器系统在典型 5 W 输出时的转换效率可达82%,超过欧盟DoE.6能效标准.
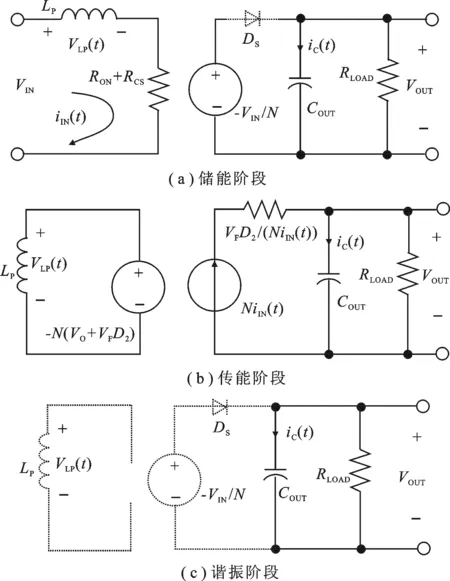
图1 非连续导通模式下各状态的等效电路
1 反激式交流-直流变换器及静态模型
1.1 反激变压器的建模
工作于非连续导通模式的反激变换器的一个开关周期可分为3个状态.图1给出了各个阶段的等效电路.
图1中,RON为功率开关管导通电阻.设VF为整流二极管的正向导通压降,D2为次级侧的导通占空比,iIN(t)为初级侧的环路电流.
在储能阶段,初级侧环路电流iIN(t)流经初级侧电感LP、功率开关管的内阻RON以及采样电阻RCS,次级侧的整流二极管反向截止,负载电流由输出电容COUT提供.根据基尔霍夫电压定律与电流定律,可以分别得到初级侧电感LP两端电压VLP(t)和流经输出电容COUT的瞬时电流iC(t):
(1)
在传能阶段,初级侧功率开关管关断,初级侧环路电流iIN(t)为零.由于次级侧整流二极管导通,因此输出电压和整流二极管的前向导通电压一起反射到初级侧作为初级侧电感LP的去磁电压.并且,在该阶段折合到副边的初级侧电流同时提供输出电容支路的充电电流和负载电流.根据基尔霍夫定律,有
(2)
在谐振阶段,该过程中次级侧电流已经降为零,导致整流二极管反向截止.此时折合到初级侧的反射电压为零且负载电流由COUT提供.同理可得:
(3)
根据状态空间平均法,忽略初级侧电感电压和次级侧输出电容电流的纹波,只考虑其稳态直流成分.根据伏-秒平衡法则,联立式(1)~式(3),得到
D1[VIN-iIN(t)(RON+RCS)]+D2[-N(VOUT+VFD2)]+D3·0=0 ,
(4)
其中,D1为功率开关段导通过程的占空比,D3为谐振阶段的占空比.
对式(4)进行化简,得
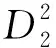
(5)
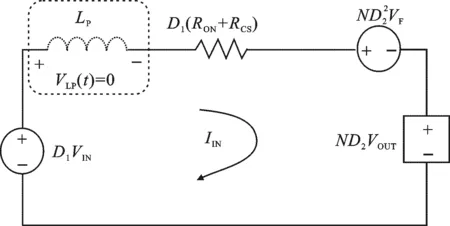
图2 方程式(5)对应的网孔电路
式(5)是根据基尔霍夫电压定律得到的,为经过平均化的一个开关周期内原边电感电压的稳态方程.可以发现,式(5)的形式与标准环路方程高度相似,该方程描述了一个包含初级侧电感的环路,环路中的各个直流电压的加和结果等于零,且该环路的电流等于IIN.因此,可以用一个网孔电路来描述式(5).具体而言,对于式(5)中的第1项,由于D1和VIN均可以看成是常量,所以D1VIN可以用一个理想电压源来表示.同理,第3项ND22VF也可以用一个理想电压源表示,只是注意该项前面的负号表示该电压源的极性与第1项对应的理想电压源的极性相反.对于式中的第2项,其在电路中的表现形式可以用一个值为D1(RON+RCS)的电阻表示.由于式(5)中的第4项与输出电压相关,因此该项在电路中的表现形式可以用一个受控电压源表示.经过上述分析,方程(5)对应的网孔电路如图2所示.
同理,对式(1)~式(3)中的电容电流部分应用安-秒平衡法则,可得
ND2IIN-(D1+D2+D3)VOUT/RLOAD=0 .
(6)
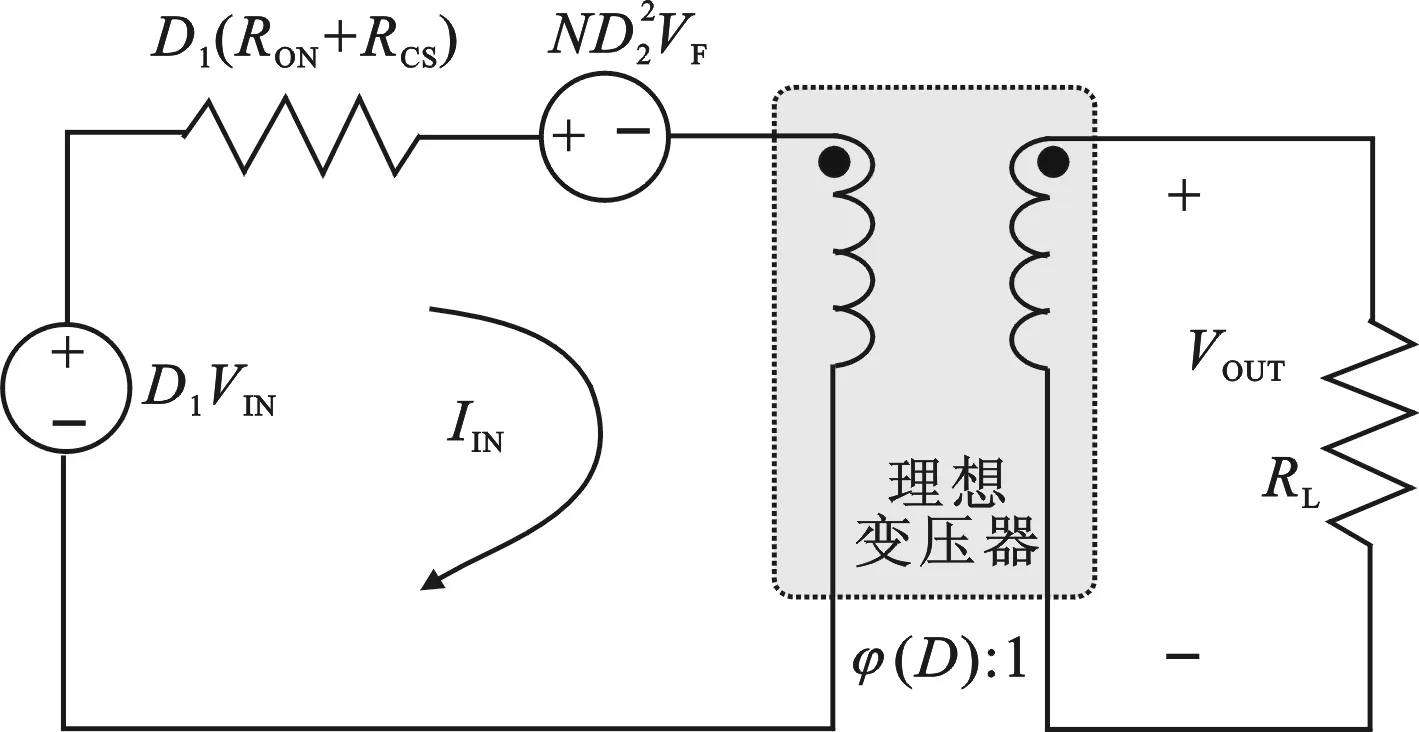
图3 反激变换器稳态模型
式(6)包含两项.第1项与初级侧环路电流有关,因此可以用一个受控电流源表征.同时,注意到D1+D2+D3=1,因此第2项意味着是一个用电压除以电阻形式表征的电流,所以该项在网孔电路中对应着一个值为RLOAD的电阻.如此可得与方程(6)对应的网孔电路.将两次得到的网孔电路合并,可得反激变换器系统稳态时的等效模型,如图3所示,其中φ(D)=ND2.
在图3所示的工作在非连续导通模式下的反激变换器稳态等效模型中,原来的反激变压器已经被理想变压器所取代,便于后期的分析与计算.同时,该模型中包含系统工作时的主要静态损耗因子,如功率开关管的导通电阻RON、初级侧电流采样电阻RCS以及整流二极管正向导通压降.与文献[9-14]中所描述的模型相比,该模型省去了复杂的控制信号运算,同时对于静态损耗的计算仍保持了较高的精确度,更适合于工程应用.
1.2 静态损耗分析
将图3的副边电路按照理想变压器性质折算到变压器的原边,可以得到原边环路电流IIN为
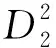
(7)
进而推导出反激变换器的静态损耗P为
P=D1(RON+RCS)+IINNVF.
(8)
根据能量守恒定律,可得占空比D2与D1之间的关系为
D2=D1[VIN/(NVOUT)]1/2.
(9)
1.3 开关损耗分析
反激变换器功率损耗中的另一主要部分是系统的开关损耗.该部分损耗特指初级侧功率开关管的导通和关断瞬间由于其两端电压与漏极电流波形在开关瞬间产生交叠因而产生的功率损耗.该部分损耗的产生是由于功率开关管不是理想的开关器件,在其各个极之间存在寄生参数,这些寄生参数导致开关瞬间的功率损耗.
对文献[15]中所述的功率开关管模型及对开关损耗的分析可得,一个周期内的开通损耗可表示为
(10)
2 功率级损耗分析
根据推导出的静态损耗和开关损耗表达式,可以得到反激变换器工作时的总损耗函数为
P=P+P.
(11)
该函数主要反映了反激变压器匝数比N、功率开关管的导通占空比D1以及开关频率fSW这3个参数对系统总损耗的影响.图4给出了MATLAB的仿真结果.
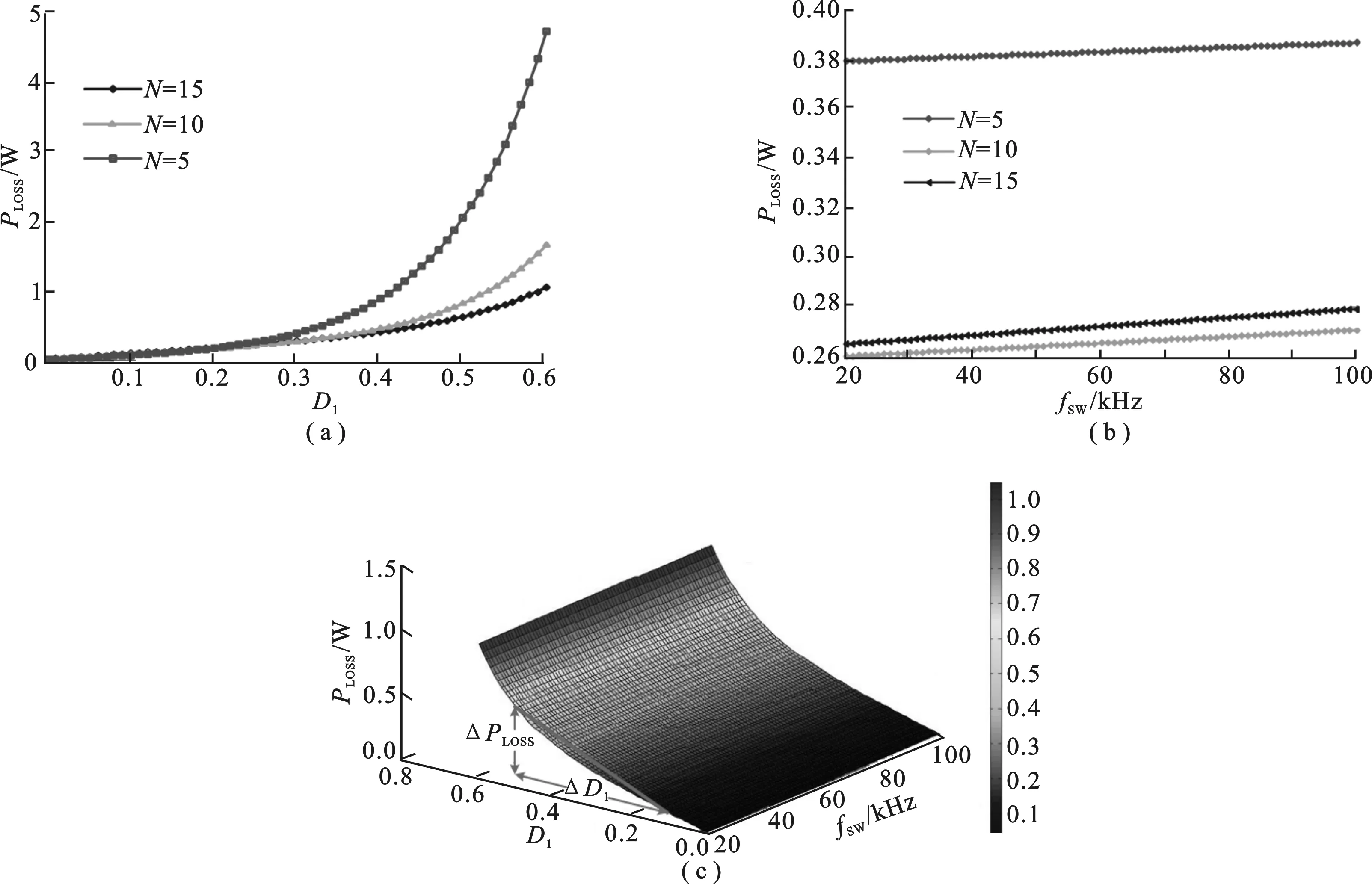
图4 反激变换器系统总损耗仿真结果
从图4(a)可以看出,D1越大,PLOSS的值就越大,且匝数比越小,系统损耗越高.从图4(b)中可知,系统损耗随着开关频率的增大而增加,且小的匝数比意味着更多的功率损失.综合图4(a)和图4(b)可知,在不影响系统安全的前提下,反激变压器的匝数比的取值应适当偏大.图4(c)给出了系统损耗与开关频率fSW以及初级侧导通占空比D1的三维曲线图,相比于开关频率,系统的导通占空比对系统总功耗有更大的影响.对于采用峰值电流模式且工作于非连续导通模式的反激变换器系统,峰值电流对应着导通占空比,而过大的导通占空比不仅会导致系统进入连续导通模式,同时也会引起严重的稳定性和安全性问题,所以其峰值电流应随着系统的负载降低而动态减小,且系统工作频率也应随着负载降低而减小,由此提升了系统的转换效率.
3 实测结果及分析
图5为对采用该控制策略的反激式交流-直流变换器流片后的芯片进行测试的结果.图5(a)为负载电流为 0.5 A 的实测波形.从图中可以看出,此时输出电压为 5.18 V,初级侧峰值电流阈值为 366 mV.图5(b)为负载电流为 2 A 的实测波形.从图中可以看出,此时输出电流为 5.06 V,初级侧峰值电流阈值为 590 mV.由此可以看出,当系统处于轻重载切换时,系统负载调整率仅为2.3%.根据测试波形可以看出,系统的初级侧峰值电流以及开关频率随负载变动而动态变化.

图5 不同负载下系统输出的实测波形
实测结果表明,系统在轻载 0.5 A 到重载 1.5 A 负载范围内,系统效率高于73%,最高效率达到83%.低输入电压下的整体效率低于高输入电压时的效率,原因在于相同输出功率时,低输入电压下的输入电流较大,导致线损及变压器损耗较高输入电压时的大.
4 结 语
笔者从降低系统功率损耗的角度研究了提升转换效率的方法.在此基础上,首先应用状态空间平均法对反激变压器进行等效处理,转换其形式使之易于进行数学分析与计算; 其次,应用基尔霍夫电压电流定律分别对初次级中的储能元件进行分析,导出其V-I方程并构建等效网孔电路; 最后将得到的初次级等效网孔电路合并成一个包含理想变压器的等效电路,至此完成对反激变换器的功率级建模.随后基于模型进行损耗分析,找出系统关键参数的取值对系统损耗的影响,并据此提出一种高效的恒压控制策略.通过Hspice仿真与实测证明,该策略与理论分析高度吻合,印证了功率级模型的精度及可靠性.
