油类污染物三维荧光光谱的瑞利散射消除方法

陈至坤，黄 微，沈小伟，程朋飞，王福斌

(华北理工大学电气工程学院，河北 唐山 063210)

0 引 言

三维荧光光谱技术具有灵敏度高、选择性好、分析速度快等优点，在油污种类及其来源鉴别方面得到了广泛的应用[1-4]。在进行荧光光谱实验时，油类物质的光谱中存在瑞利散射光，其波长与入射光相同，光强与入射光波长的四次方成反比，散射光的强度有时甚至强于荧光，会掩盖和干扰待测荧光物质本身的荧光峰，降低三维荧光光谱对混合油类污染物的鉴别能力，影响分析结果，必须予以消除[5-8]。常用的消除瑞利散射的方法有置零法、空白扣除法、Delaunay三角形内插值法等[9]。置零法就是根据瑞利散射在荧光光谱中出现的位置比较固定，将发射波长（EM）等于激发波长（EX）及其附近区域的值置零；该方法在消除干扰的同时会损失散射区域的荧光信息，不利于后续光谱分析的准确性。空白扣除法是将样本溶液的光谱矩阵数据减掉溶剂的光谱矩阵数据，从而消除瑞利散射；该方法具有操作简便、计算简捷的优点，是实验室中常被采用的方法之一。Delaunay三角形内插值法的原理是应用散射峰周围的数据拟合值替换掉散射区域数值，达到消除瑞利散射的目的[10]；该方法可以有针对性地处理散射区域数据而不改变非散射区的荧光强度，保证了荧光物质光谱信息的真实性，是一种应用较为普遍的消除瑞利散射的方法。

本文提出MDR法分别结合主成分分析（PCA）、平行因子分析（PARAFAC）对单组分及多组分矿物油四氯化碳溶液三维荧光光谱的瑞利散射进行处理，并与空白扣除法、Delaunay三角形内插值法消除瑞利散射效果进行对比，验证了MDR法用于油类三维荧光光谱去除瑞利散射时的可行性及优越性。

1 基本原理

1.1 MDR-PCA

单个荧光光谱激发-发射矩阵（EEM）符合双线性，可采用主成分分析法对EMM进行解析[11]。MDR-PCA法的原理是首先将荧光数据中的散射干扰数据全部扣除，之后利用主成分分析（PCA）迭代过程对扣除数据进行重构修复后补全数据。MDRPCA方法可分为以下7个主要步骤[12]：

1）识别EEM光谱矩阵Z中的散射区域，对于瑞利散射，其一般为|EM－EX|≤10～15 nm的对角线区域；

2）设置与Z同样大小的加权矩阵W，其中对应矩阵Z中散射数据的部分设为0，其余部分设为1；

3）将光谱散射区域的数据设为缺损数据，可置初始值如0或NaN；

4）在EEM矩阵Z的主成分分析（PCA）迭代过程中，用每一步计算出的得分向量t和载荷向量p重构矩阵中的缺损数据：

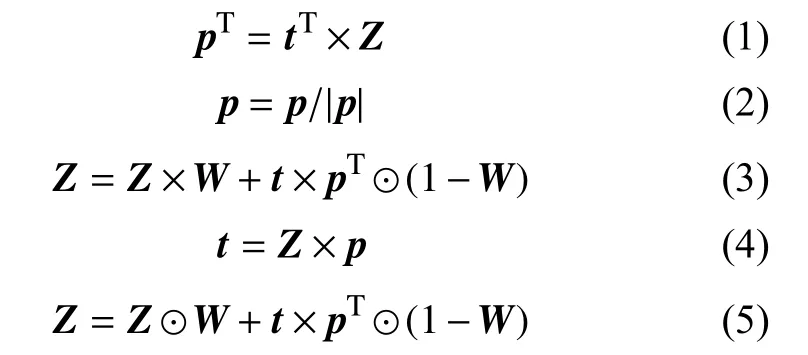
5）迭代计算至收敛，收敛损失函数不计入缺损数据部分；

7）用主成分重构的缺损区域替换散射区域，即得到修复的光谱矩阵X：

该方法在消除散射干扰的同时充分利用了荧光物质光谱矩阵中的有效信息对散射区完成了修复，有利于实现三维荧光光谱的无损分析。

1.2 MDR-PARAFAC

多个样本的EEM组成三维数据矩阵（EEMs）符合三线性，利用平行因子分析进行分解可以得到样品中各组分的特征光谱与相对浓度。三线性模型表达式为：

εijk——误差矩阵E中的对应元素；

aif、bjf、ckf——载荷A、B、C矩阵中的元素。

该三线性模型也可写成以下矩阵形式：

式中：X··k——X中的第k个EEM光谱；

A——F个组分的激发光谱矩阵；

B——F个组分的发射光谱矩阵；

c(k)——浓度矩阵C的第行；

E··k——误差矩阵E中的第k个矩阵。

MDR-PARAFAC计算过程包括以下9个步骤[12]：

1）识别EEM光谱矩阵散射区域，对于瑞利散射一般为|EM - EX| ≤ 10～15 nm 的对角线区域；

2）设置与EEM矩阵相同大小的加权矩阵W，其中对应EEM矩阵中缺损数据的部分设为0，其余部分设为1；

3）将光谱散射区域的数据设为缺损数据，置初始值如0；

4）确定组分数F；

5）初始化矩阵A和B；

6）由X、A和B估计C：

其中Z·k为缺损数据重构矩阵，由下式计算：

7）由X、B和C估计A：

8）由X、A和C估计B：

2 实验分析

2.1 实验仪器

选用日立公司生产的Hitachi F-7000型荧光光谱分析仪。设定激发波长范围250～430 nm，发射波长范围 310～520 nm，步长均为 5 nm，狭缝宽度均为10 nm；扫描速度 12 000 nm/min，PMT 电压 400 V，响应时间为自动，自动校正扫描光谱。

2.2 样品配置

选取市场购置的0#柴油、95#汽油和普通煤油作为污染物质，CCl4作为溶剂来配制实验样品。用电子天平称量柴油、汽油和煤油各1 g分别置于100 mL容量瓶中，加入CCl4溶解稀释后得到3种油的100 mg/L标准溶液；分别量取不同体积的上述溶液于容量瓶中混合并加入CCl4溶剂定容配制成不同浓度的样品，并对其进行编号：1#～2#为纯组分样品，3#～12#为混合样品。各样品中矿物油的浓度如表1所示。

3 结果与讨论

3.1 单组分荧光光谱瑞利散射的消除

应用PCA法能够对EEM矩阵的荧光激发光谱和发射光谱进行提取[16]；但需要注意的是，若荧光光谱中存在散射干扰时，会引起光谱失真影响实验的精确度。图1为采用空白扣除法得到的柴油和汽油（样品1和样品2）四氯化碳溶液的等高线光谱，以及用PCA方法提取的单组分激发、发射光谱；蓝色实线表示不含散射的纯组分真实光谱，红色虚线表示处理后提取的激发、发射光谱。由图可见采用空白扣除法无法将瑞利散射完全消除，柴油和汽油荧光光谱中仍可直观的观察到存在着部分瑞利散射，导致提取到的光谱在局部边缘区发生了显著失真现象，提取光谱的轮廓显著偏离真实光谱。

采用Delaunay三角形内插值法消除瑞利散射后的柴油和汽油四氯化碳溶液的等高线光谱以及提取的激发、发射光谱见图2。由图可知，经过处理后，瑞利散射基本上被消除；存在于散射区域的荧光数据得到了有效拟合，还原度较高。与图1相比，光谱失真现象得到明显改善。

表1 样品中油类物质的浓度 mg/L

图1 采用空白扣除法消除瑞利散射后的等高线光谱、激发和发射光谱

图2 用Delaunay三角形内插值法消除瑞利散射后的等高线光谱、激发和发射光谱

为了精确消除瑞利散射，采用MDR-PCA法，首先将 |E M−EX|≤10 nm区域设定为数据缺损区并进行迭代修复处理，而后得到等高线光谱和提取的激发、发射光谱，如图3所示。对两者光谱进行比对可知，提取光谱与真实光谱已产生了相当高的重叠率，数据修复拟合的效果良好，有效达到了消除瑞利散射的目的。

3.2 多组分荧光光谱瑞利散射的消除

多个样本荧光光谱构成的立方阵符合三线性，使用三线性分解方法可同时解析出各组分的特征光谱和浓度信息。PARAFAC是三线性分解的经典方法之一。

采用空白扣除法消除瑞利散射后散射信号仍比荧光信号强得多，由于散射数据不符合三线性，用PARAFAC进行三线性分解得到各组分激发光谱、发射光谱和浓度曲线显著偏离真实光谱（结果未列出）。采用Delaunay三角形内插值法消除瑞利散射后用PARAFAC进行三线性分解得到各组分激发光谱、发射光谱和浓度曲线如图4所示。可见，解析光谱与真实光谱吻合度较好，瑞利散射基本上被消除，存在于散射区域的荧光数据得到了有效拟合，还原度较高，光谱失真现象得到明显改善。

为了精确消除瑞利散射，设置|EM - EX| ≤ 10 nm区域为数据缺损区，用MDR-PARAFAC对柴油、汽油和煤油混合物的三维荧光光谱矩阵进行三线性分解，图5显示激发光谱和发射光谱的解析解与原谱基本重合，浓度解也与预测浓度一致，浓度值偏差较小。

综上，MDR-PARAFAC法能够充分利用荧光数据并有效减小数据偏差，实现更高的光谱重叠率，具有一定的普适性，是一种更为理想地消除散射的方法。

4 结束语

散射峰是影响三维荧光光谱信息读取、精确分析数据的主要干扰因素之一，开展室内小规模荧光分析实验，分别采用空白扣除法、Delaunay三角形内插值法和MDR法消除油类污染物三维荧光光谱中存在的瑞利散射后利用平行因子分析进行三线性分解。对消除效果进行比对分析可得，MDR法消除瑞利散射更为彻底，与真实光谱重叠率更高，方法更具优越性。

图3 MDR-PCA消除瑞利散射后的等高线光谱、激发和发射光谱

图4 采用Delaunay三角形内插值法消除瑞利散射

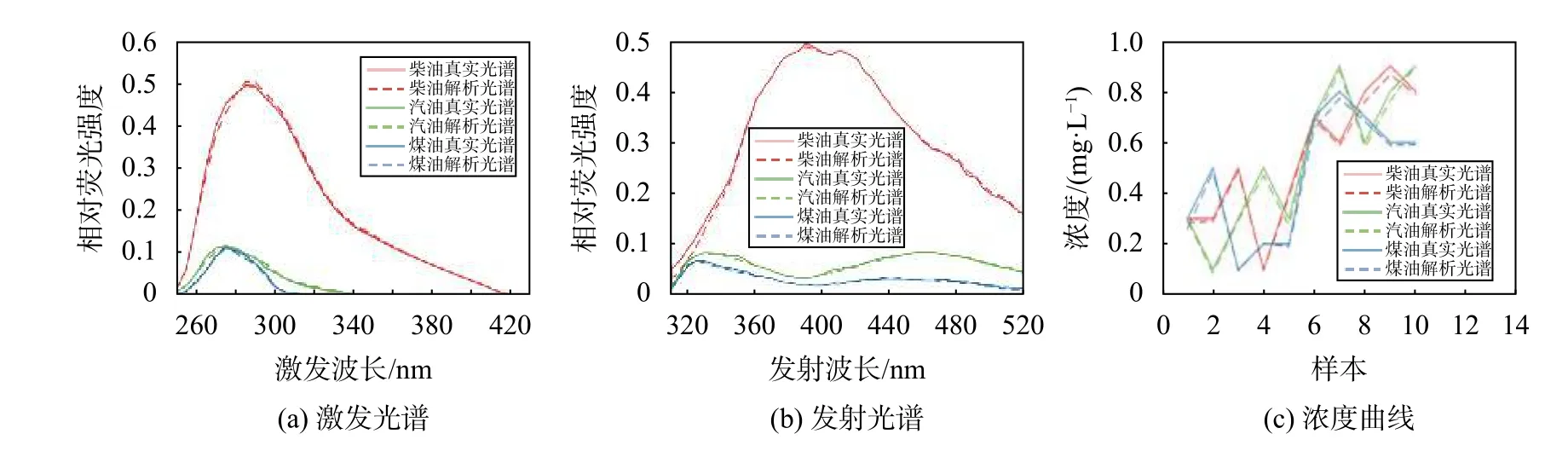
图5 采用MDR-PARAFAC法消除瑞利散射