例析矢量合成与分解在解题中的应用——高考试题研究

黑龙江 沙希文

矢量的合成法与分解法是高中物理最重要的解题方法之一，矢量的合成与分解要遵循平行四边形定则，通过作矢量图来揭示物理过程、物理规律，具有形象直观、简单明了等优点。高中物理从位移和路程的异同开始区分矢量和标量，并逐步引入了矢量的合成与分解法，之后又通过对速度、加速度，力和运动的合成与分解逐渐把这一方法延伸开来，接下去是电场强度和磁感应强度矢量问题的解决，高考中经常出现此类题目。现以具体的高考题为例，剖析矢量的合成与分解法在高考解题中的应用。

一、共点力的合成与分解

共点力平衡问题是力学的重点知识，能够很好地考查合成与分解，在历届高考试题中都会出现，力的分解，动态图解，正交分解等问题都是关于共点力的合成问题。

【例1】(2018·天津卷第7题)明朝谢肇淛的《五杂组》中记载：“明姑苏虎丘寺塔倾侧，议欲正之，非万缗不可。一游僧见之曰：无烦也，我能正之。”游僧每天将木楔从塔身倾斜一侧的砖缝间敲进去，经月余扶正了塔身。假设所用的木楔为等腰三角形，木楔的顶角为θ，现在木楔背上加一力F，方向如图1所示，木楔两侧产生推力FN，则

( )

图1

A.若

F

一定，

θ

大时

F

N

大

B.若F一定，θ小时FN大

C.若θ一定，F大时FN大

D.若θ一定，F小时FN大

【答案】BC

图2

【解题指导】由于木楔处在静止状态，故可将力F沿与木楔的斜面垂直且向上的方向进行分解，根据平行四边形定则，画出力F按效果分解的图示。并且可据此求出木楔对塔两边产生的压力。对力进行分解时，一定要分清力的实际作用效果的方向如何，再根据平行四边形定则或三角形定则进行分解即可。

【例2】(2017·全国卷Ⅱ第16题)如图3，一物块在水平拉力F的作用下沿水平桌面做匀速直线运动。若保持F的大小不变，而方向与水平面成60°角，物块也恰好做匀速直线运动。物块与桌面间的动摩擦因数为

( )

图3

【答案】C

【解题指导】此题考查了正交分解法在解决平衡问题中的应用问题；关键是列出两种情况下水平方向的平衡方程，联立即可求解。

二、库仑力和磁场力的合成与分解问题

库仑力和磁场力的合成与分解也和力一样遵守平行四边形定则，在电场和磁场力的考查中需要学生的综合能力，需要考虑电性，距离的大小，以及导线间的作用力方向等，比单纯考查力的合成与分解，更能看出学生的能力。

【例3】(2018·全国卷Ⅰ第16题)如图4，三个固定的带电小球a、b和c，相互间的距离分别为ab=5 cm，bc=3 cm，ca=4 cm。小球c所受库仑力的合力的方向平行于a、b的连线。设小球a、b所带电荷量的比值的绝对值为K，则

( )

图4

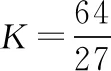
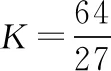
【答案】D

【解析】画出c的受力图如图5两种情况，从力的方向可以判断a、b的电荷异号。

图5

【解题指导】此题以库仑定律为基础考查矢量合成思想，关键还是得判断力的方向，根据条件正确画出力的方向，根据矢量合成和几何关系找出力的关系，再根据库仑定律求出电荷量的比值。

【例4】(2017·全国卷Ⅰ第19题)如图6，三根相互平行的固定长直导线L1、L2和L3两两等距，均通有电流I，L1中电流方向与L2中的相同，与L3中的相反。下列说法正确的是

( )

图6

A．L1所受磁场作用力的方向与L2、L3所在平面垂直

B．L3所受磁场作用力的方向与L1、L2所在平面垂直

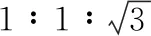
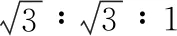
【答案】BC

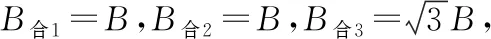
图7 图8 图9

【解题指导】根据左手定则和右手螺旋定则可以得到两个电流之间的相互作用力的规律：同向电流相互吸引，反向电流相互排斥。根据力的平行四边形定则可以进行合成。

三、磁感应强度的合成与分解问题

( )

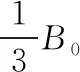
图10

【答案】AC

【例6】(2017·全国卷Ⅲ第18题)如图11，在磁感应强度大小为B0的匀强磁场中，两长直导线P和Q垂直于纸面固定放置，两者之间的距离为l。在两导线中均通有方向垂直于纸面向里的电流I时，纸面内与两导线距离均为l的a点处的磁感应强度为零。如果让P中的电流反向、其他条件不变，则a点处磁感应强度的大小为

( )

【答案】C

图12 图13

【解题指导】无限长通电导线在周围产生的磁场的磁感应强度与导线中的电流大小成正比，与到导线的距离成反比。电流周围磁场方向可以用安培定则判断，画出磁感应强度的方向，利用平行四边形定则进行计算。

四、运动的合成与分解问题

运动的合成与分解，实际是描述运动的物理量的合成与分解，涉及速度、位移和加速度的合成与分解，合成与分解是解决平抛运动的方法，也是解决复杂运动问题的基本方法。

( )

A．2倍 B．4倍 C．6倍 D．8倍

【答案】A

【解题指导】在斜面上平抛，当落回斜面时，斜面的底角就为位移与水平方向的夹角，根据水平和竖直位移公式，合成平行四边形，根据几何关系可以很好地找到速度大小关系。

【例8】(2015·全国卷Ⅱ第24题)如图14，一质量为m、电荷量为q(q>0)的粒子在匀强电场中运动，A、B为其运动轨迹上的两点。已知该粒子在A点的速度大小为v0，方向与电场方向的夹角为60°；它运动到B点时速度方向与电场方向的夹角为30°。不计重力。求A、B两点间的电势差。

图14

【解析】设带电粒子在B点的速度大小为vB，粒子在垂直于电场方向的分速度不变，即

vBsin30°=v0sin60°

设A、B两点间的电势差为UAB，由动能定理有

【解题指导】本题利用了速度的分解，根据水平和竖直两个分运动的分解，再根据加速度关系可知，竖直方向重力不计，所以速度不变，可以求出末速度，之后才能利用动能定理把电势差求出。所以本题的关键还是矢量的合成运算。解题指导：对于绳连物体的运动，把物体的实际速度分解为沿绳方向和垂直于绳方向的两个分速度。