变力做功的几种求法
2018-12-06陕西孙冬子
陕西 孙冬子
功是中学物理中的重要概念,而高中阶段所学功的表达式W=Fscosθ只适用于求恒力做功,对于变力做功的计算没有固定公式可用,所以求变力做功只能另寻他法。变力做功又是高考中的常考点,同时对同学们而言变力做功又是一个难点,其之所以难是在于题目的复杂性、灵活性、多变性以及方法的多样性,因此变力做功题目让同学们感到非常棘手。下面就变力做功方法做一归纳总结。
一、利用公式W=Pt求变力做功
在一些题目中力虽然不断变化,但是该力的功率却保持不变,如机车启动、起重机起吊重物等,此类问题就可以通过W=Pt进行求解。
【例1】一列车的质量m=5.0×105kg,在平直的轨道上以恒定功率3 000 kW加速行驶,当速度由v1=10 m/s加速到所能达到的最大速度v2=30 m/s时,共用了2 min,则在这段时间内列车前进的距离是多少?
【解析】列车以恒定功率加速行驶,由P=Fv可知其牵引力不断减小,所以此过程为变加速直线运动,所以不能用牛顿运动定律求解,结合题意可以考虑用动能定理求解。
依题意由动能定理
又v2是最大速度则
联立解得s=1 600 m
【例2】新中国成立前后,机械化生产水平较低,人们经常通过驴拉磨的方式把粮食加工成粗面食用,如图1所示,假设驴拉磨的平均作用力为F,运动的半径为R,那么驴拉磨转动一周所做的功?
图1
【解析】驴拉磨简化模型如图2所示,拉力沿切线方向且与速度方向相同,由P=Fv可知拉力的功率恒定,所以可以用W=Pt求解。由题意得
W=Pt
P=Fv
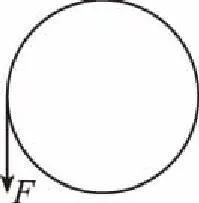
图2
联立解得W=2πRF
该类题目多数老师采用微元法求解,但在具体教学中发现部分同学对微元法理解不够深刻,所以用微元法讲解收效甚微,且求解方法越多越使同学眼花缭乱更加无所适从,而用W=Pt求解同学更易理解接受。可见当物体以恒定速率做曲线运动,受到大小以及与速度方向夹角恒定力作用,该力所做的功也可以用W=Pt求解。
二、转变力做功为恒力做功
在一些题目中我们可以通过转换研究对象或通过数学运算对模型进行简化,可以将变力转化为恒力,然后利用W=Fscosθ求解。
【例3】如图3所示,质量为m的小车以恒定速率v沿半径为R的竖直圆轨道运动,已知小车与竖直圆轨道间的动摩擦因数为μ,试求小车从轨道最低点运动到最高点的过程中,克服摩擦力做的功。
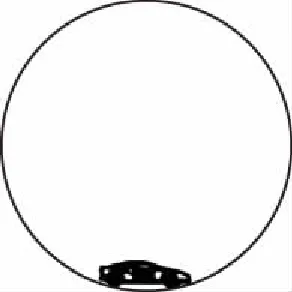
图3
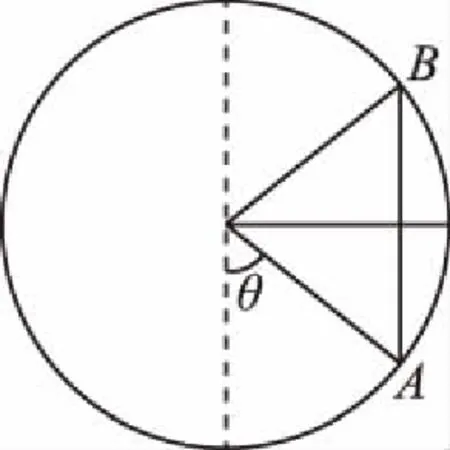
图4
【解析】小车从最低点运动到最高点的过程中,由于小车和轨道间的压力不断变化,所以小车运动过程中所受摩擦力大小不断变化。我们分析下看能否将此变力转变为恒力。
当小车通过图4中的A、B两点有
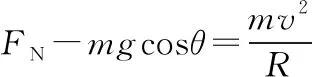
F摩=μFN
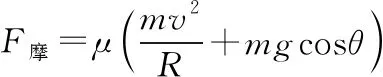
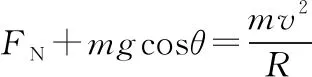
F摩=μFN
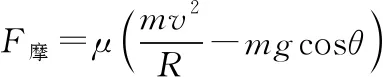
由对称性可得,关于水平半径上下对称圆弧所受摩擦力等效为
则W=F摩πR=μπmv2。
此方法也适用于轻质细绳跨过定滑轮拉一物体,而绳的一端为变力另一端为恒力,可以将一端变力做功转换为另一端的恒力做功进行求解。
三、图象法
在F-s图象中,图象与坐标关于某段位移所围面积表示该段位移内力所做的功,所以当力和位移在一条直线上且力为变力,我们就可以借助F-s图象求解。
【例4】用铁锤把小铁钉钉入木板,设木板对钉子的阻力与钉子进入木板的深度成正比,已知铁锤第一次将钉子钉入深度为d,如果铁锤第二次敲钉子时对钉子做功与第一次相同,那么第二次钉子进入木板的深度是多少?
【解析】由于钉子受到阻力与钉子进入木板的深度成正比,则阻力与钉子进入木板深度的函数图象是一条过原点的倾斜直线,因此可用F-s图象求解,图象如图5所示,则
f1=kd
f2=k(d+d′)

图5
由于两次钉钉子做功相等,所以有
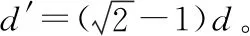
由于本题中力随位移均匀变化,所以有人想到用平均值法求解,但在求第二次打击时所受平均力时容易出错,而用图象法则可以避免此问题,所以在求变力做功时可以将两种方法合二为一,利用图象法可以有效防止因分析不到位而引发错误。
四、功能关系
功是能量转化的量度,做了多少功就有多少能量发生转化,因此功和能之间存在密切的联系,所以在求解变力做功时经常用到功能关系。在功能关系中用的最多的应该是动能定理,由于动能定理只需考虑始末状态而不管中间运动过程,并且应用比机械能守恒定律方便,所以动能定理是变力做功的首选方法。其次是能量守恒,由于能量守恒是自然界普遍遵从的守恒法则,所以在求解变力做功时也经常用到能量守恒。
【例5】如图6所示,在长为L的轻杆中点A和端点B各固定一质量均为m的小球,杆可绕无摩擦的轴O转动,使杆从水平位置由静止释放。求当杆转到竖直位置时,轻杆对A、B两球分别做了多少功?
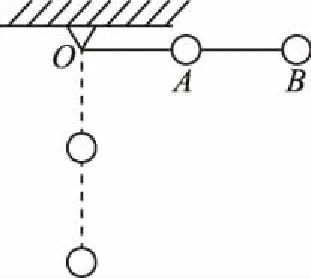
图6
【解析】由于A、B两球固定在同一木杆上,且A在杆的中点处,所以当杆绕O点旋转时B球的速度大小是A球速度的2倍。设运动到竖直位置时A球的速度为v。对A、B两球组成系统应用动能定理有
设杆对B球做功为WB,对B球应用动能定理有
联立解得WB=0.2mgL
由于木杆为轻质杆,所以A、B两球组成系统能量守恒,杆对B做多少正功则对A做多少负功,设杆对A球做功为WA,则有
WA=-0.2mgL。
五、微积分
高中阶段已经学习了简单的微积分,而功本身就是力对位移积累的物理量,所以当已知力和位移的函数关系时就可以用微积分进行求解。
上面例4微积分求解法
【解析】由于阻力与钉子进入木板的深度成正比,所以有
f阻=kx
由于铁锤第二次敲钉子时对钉子做功与第一次相同,设第二次敲打钉子进入木板深度为d′,则有
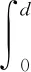
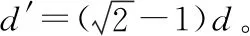
从微积分角度看微元法,当物体在大小以及与速度间夹角恒定的力作用下做曲线运动时,该力所做功大小等于力与路程的乘积。

