基于土拱理论的地下连续墙护壁泥浆最小重度计算

蔡兵华，李忠超，杨 新，孙金山，孙 聪，林 曜

(1.武汉市市政建设集团有限公司，湖北 武汉 430023;2.中国地质大学(武汉)工程学院，湖北 武汉 430074)

地下连续墙是基坑的重要围护结构形式，具有承重、挡土以及截水抗渗等作用，同时还可作为永久结构的外墙。

地下连续墙是在土质沟槽的泥浆中现浇成型的钢筋混凝土结构，其施工质量控制难度较高，而施工时保持槽壁稳定，防止槽壁坍塌是施工质量核心内容之一。泥浆槽壁在浇筑混凝土过程中会产生坍塌，坍塌土体混入混凝土中会造成墙体缺陷，甚至会使墙体内外贯通，成为管涌通道。泥浆槽壁坍塌除了影响工程质量外，还将导致地面沉陷，使挖槽机械倾覆，对邻近的建筑物和地下管线造成破坏。因此，地下连续墙泥浆槽壁的稳定性分析与控制问题是地下工程中一个重要的研究课题。

针对地下连续墙泥浆槽壁的稳定性问题，国内外学者开展了一些研究工作。如姜朋明等[1]采用应力极限状态分析方法，探讨了时间效应对地下连续墙泥浆槽壁稳定性的影响；刘国彬等[2]分析了超载作用对地下连续墙泥浆槽壁稳定性的影响；王轩

等[3]探究了不同地下连续墙泥浆槽壁整体稳定性分析方法的差异和适用性；张厚美等[4]提出了最危险破坏面的三维分析法,同时还利用三维分析法对影响地下连续墙泥浆槽壁稳定性的主要因素进行了研究。此外，国内外的一些学者也针对该问题提出了不同的分析方法[5-12]。但是，由于以往针对地下连续墙泥浆槽壁稳定性的分析方法多是基于多破裂面的近似假定而提出的，其适用性和可靠度仍存在不同程度的缺陷。为此，本文通过对地下连续墙泥浆槽壁破裂面几何形态的理论分析，构建了泥浆槽壁潜在破裂面的极限平衡模型，研究了护壁泥浆最小重度的计算方法和泥浆槽壁稳定性的分析方法，以为工程施工提供参考。

1 地下连续墙泥浆槽壁潜在破裂面的形态特征分析

地下连续墙泥浆槽壁具有一定的自稳性，但随着槽体深度的增加，水平向土压力增大，不可避免地会产生纵向的破裂面。工程实践和理论分析表明，地下连续墙泥浆槽壁破裂面的形态特征与土拱效应密切相关。当地下连续墙泥浆槽所处松散介质向槽内产生相对位移或有相对位移的趋势时，土拱效应即可产生。因此，本文在刘丹珠等[13]关于土洞坍塌机制分析的基础上，对地下连续墙泥浆槽壁潜在破裂面的形态特征进行分析。

1. 1 地下连续墙拱状破裂面的边界轴线方程

设地下连续墙泥浆槽壁向其内部变形时土体自发形成土拱，土拱形态如图1所示。图中：作用在土拱上的土体的厚度为H，拱高为h，拱跨为L，土体容重为γ，土拱所受的竖向分布荷载为qc,qc=γH。

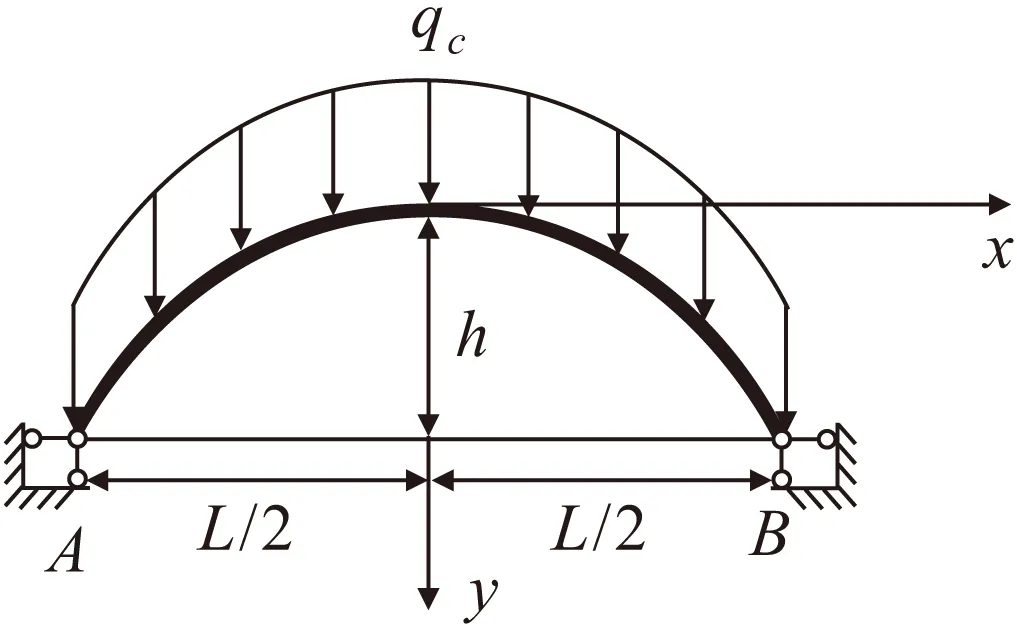
图1 土拱力学模型Fig.1 Mechanical model of soil arch

设在竖向荷载作用下，拱的弯矩M处处为0，可得到拱轴线方程为

(1)

式中：qc为土拱所受的竖向分布荷载；FH为水平支座反力。

解得拱轴线方程的通解为

(2)

其边界条件为

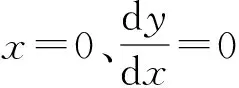
将边界条件代入公式(2)，可得到拱轴线方程通解表达式为

(3)

式中：H为上覆土体的厚度；FH为水平支座反力。

为了计算水平支座反力FH，通过建立支座处的静力平衡方程，求出水平支座反力FH和竖直支座反力FV的近似解为

(4)

(5)

式中：l为泥浆护壁槽段的长度。

将公式(4)代入公式(3)，可得到拱轴线方程的近似解为

(6)

1. 2 地下连续墙拱状破裂面的破裂厚度

形成稳定土拱后，拱圈以下土体在没有支护且底部存在倾斜滑裂面时将会发生坍塌，而拱下土体的体积是判别其稳定性的重要参量。根据土拱中土体剪应力应小于其抗剪强度的条件，土拱拱脚处的支座反力处于极限平衡状态时，应满足摩尔库仑屈服条件：

(7)

式中:c为土体的黏聚力，无黏性土中，土体的黏聚力c=0；φ为土体的有效内摩擦角。

将公式(4)和(5)代入公式(7)，可得：

(8)

求解方程式(8)并取其中的合理解，可得无黏性土拱状破裂面的最大破裂厚度hncmax为

(9)

黏性土中，土体的黏聚力c不为0，将公式(4)和(5)代入公式(7)，可得：

(10)

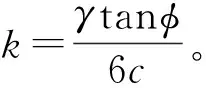
求解方程(10)并取合理解，可得黏性土拱状破裂面的最大破裂厚度hcmax为

(11)

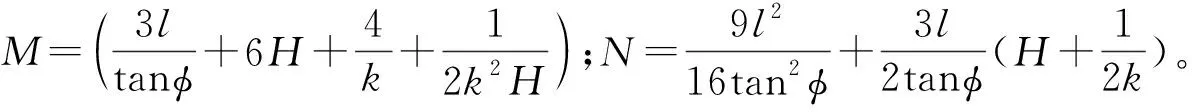
1. 3 地下连续墙拱形破裂体横断面的形态分析

对于地下连续墙而言，泥浆槽壁失稳时土体发生水平位移，此时土拱呈水平状，土拱的拱肩为泥浆护壁槽段两侧未开挖土体。

设地下连续墙泥浆槽开挖深度为Z，土体的侧压力系数为λ，根据土拱的空间效应特征，地下连续墙侧壁发生横向破裂的最大深度大约为

H=Z-1.5l～Z

(12)

上式中，l为泥浆护壁槽段的长度，该处的水平向荷载则相当于λH厚土层产生的，因此不考虑地下水时厚度为z处的竖向土压力为Pz，水平向土压力为λPz，则水平向承受的土压力与厚度为λz土层的竖直向土压力相同，可得厚度为z处的拱状破裂面的轴线方程为

(13)

深度H处，无黏性土横向拱状破裂面的最大破裂厚度为

(14)

深度H处，黏性土横向拱状破裂面的最大破裂厚度为

(15)

深度H处，对拱状破裂面的轴线方程进行积分，可得拱形破裂体横截面的面积如下：

对于无黏性土：

(16)

对于黏性土：

(17)

2 地下连续墙泥浆槽壁稳定性分析方法

地下连续墙泥浆槽的开挖是在泥浆保护下进行的，泥浆产生的水平向压力能有效平衡一部分水平向的土压力，起到阻止地下连续墙槽壁发生水平位移甚至发生破裂的作用，或者说是阻止土拱效应的发生。

目前分析地下连续墙泥浆槽壁稳定性的方法较多，常用的泥浆槽壁破裂体几何形态模型有抛物线柱体、半圆柱体、楔形体等模型。由于不同模型的假设条件不同，因此得到的结果也不同。本文基于上述地下连续墙泥浆槽壁水平土拱特征的理论分析，对地下连续墙泥浆槽壁的稳定性进行分析。

2. 1 三维破裂体受力特征分析

设地下连续墙泥浆槽壁的破裂体为一具有倾斜滑动面的三维实体(见图2)，滑动面与水平面夹角为α，拱形破裂面的开口朝向泥浆槽，开口宽度等于泥浆护壁槽段长度l，破裂面顶点到泥浆槽壁的距离即破裂厚度为h，地下连续墙泥浆槽的开挖深度为Z。

图2 地下连续墙泥浆槽壁破裂体的几何形态模型Fig.2 Geometric model of the destroyed object of diaphragm wall slurry trench

泥浆槽壁破裂体所受的力包括破裂体自重W、地面荷载P、槽内泥浆压力与地下水压力的合力ΔP、拱状破裂面上侧壁土体黏聚力的合力Pf、滑动面上的抗剪力Ps以及滑动面的法向反力N等，见图3。

图3 地下连续墙泥浆槽壁破裂体的受力模型Fig.3 Mechanical model of the destroyed object of diaphragm wall slurry trench

(1) 破裂体自重W：破裂体的自重W等于破裂体的体积乘以土的重度。地下水位以上破裂体的体积为

Vu=S(Z-mz)

(18)

式中:S为拱形破裂体横截面的面积;Z为地下连续墙的泥浆槽开挖深度；mz为地下水位到槽底的距离。

滑动面DC以下的蹄状体积(DCE)为拱状破裂面与倾角为α的滑动面所围成的体积，即：

(19)

将公式(13)代入公式(19)，可得到：

(20)

式中:h为拱状破裂面的最大破裂厚度，其中无黏性土为hnc，黏性土为hc。

地下水位以下破裂体的体积为

VD=Smz-VDEC

(21)

则破裂体的自重为

W=Vuγ+VD(γ-γw)

(22)

将公式(18)、(21)代入公式(22)，并整理得：

W=S(Z-mz)γ+(Smz-VDEC)(γ-γw)

(23)

式中:γ为土的重度;γw为地下水的重度。

(2) 槽内泥浆压力与地下水压力的合力ΔP：泥浆压力与地下水压力对破裂体的合力ΔP为

(24)

式中:γc为护壁泥浆的重度。

(3) 破裂体拱状破裂面上侧壁土体黏聚力的合力Pf：将破裂体横截面的拱轴线简化为微小的阶梯状(见图4)，当破裂体滑动时，平行于x轴方向的微元阶梯面上作用有黏聚力，可抵抗破坏体的滑动变形。由图4可见，破裂体拱状破裂面上整个侧壁可提供土体黏聚力的面积为其向x轴方向的投影面积之和，即等于图3中ABCD面积的2倍[4]，则有：

Af=2Zh-h2tanα

(25)

则拱状破裂面上侧壁土体黏聚力的合力为

Pf=(2Zh-h2tanα)c

(26)

图4 土体黏聚力作用面积示意图Fig.4 Schematic of the soil cohesion effect area

(4) 滑动面上的抗剪力Ps:滑动面上的抗剪力Ps等于滑动面摩擦力与黏聚力之和，即：

Ps=Ntanφ+Acc

(27)

其中，滑动面的法向反力N为

N=(W+P)cosα+ΔPsinα

(28)

滑动面的面积Ac为

(29)

将公式(28)和(29)代入公式(27)，可得：

(30)

2. 2 护壁泥浆最小重度的计算

当滑动面处于极限状态时，得到的静力平衡方程为

(W+P)sinα=ΔPcosα+Ps+Pf

(31)

将公式(23)、(24)、(26)、(30)代入公式(31)，可得到同时适用于黏性土和非黏性土中泥浆最小重度(临界重度)的计算公式为

(32)

由于滑动面倾角越大，破裂体越容易滑动，因此假定滑动面下边缘位于槽底、上边缘位于地表时，滑动面的倾角为

(33)

3 算例分析

为了对上述得到的地下连续墙槽壁泥浆的最小重度计算公式的可靠度进行验证，本文分别采用文献[3]和文献[4]中的算例，对黏性土和非黏性土中地下连续墙护壁泥浆的最小重度或泥浆槽壁的稳定系数进行了计算与对比分析。

3. 1 黏性土

地下连续墙泥浆槽的开挖深度Z为37.5 m，泥浆护壁槽段的长度l为6 m，土的重度γ为18 kN/m3，土体的黏聚力c为10.7 kPa、土体的内摩擦角φ为23°，地下水位标髙hw为3.19 m，地面超载P为40 kN/m2。本文分别利用文献[4]中的半圆柱法、抛物线法等和本文算法对地下连续墙护壁泥浆的最小重度进行了计算与对比，其计算结果见表1。

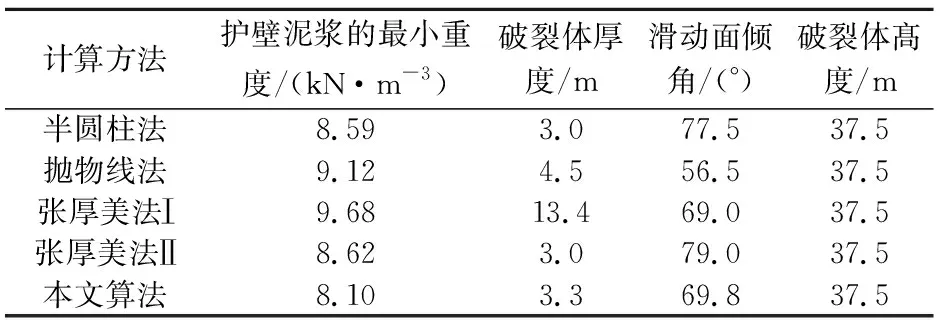
表1 不同方法计算的护壁泥浆的最小重度对比

由表1可知，对于黏性土，各种方法计算得到的护壁泥浆的最小重度存在一定的差距，本文算法的计算结果与半圆柱法较为接近，且其计算值最小，地下连续墙拱形破裂体的最大破裂厚度hc为3.3 m，相对于文献[4]计算得到的13.4 m更为合理。

3. 2 无黏性土

对于无黏性土，则根据文献[3]中的4个算例采用不同方法对地下连续墙泥浆槽壁的稳定系数Fs进行了计算与对比，地下连续墙泥浆槽的开挖深度为15 m，算例的计算参数见表2，各种方法计算得到的结果见表3。

表2 4个算例的计算参数[3]

表3 不同方法计算结果的对比

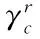
但由于Washbourne算法假定潜在破裂体呈假定的“三棱柱”，其与实际破坏形态存在一定的差异，缺乏理论支撑，因此计算得到的槽壁稳定性和可靠性难以保证。

还需要指出的是，本文算法计算得到的护壁泥浆的最小重度略偏于危险，因此工程实际中应采用重度大于该计算值的泥浆。

4 结 论

根据地下连续墙泥浆槽壁的失稳破坏特征，分析了泥浆槽壁“土拱”状破裂面的形态特征，并在此基础上基于极限平衡原理，提出了一种地下连续墙护壁泥浆最小重度的计算方法，该方法适用于黏性土和非黏性土。算例表明：该方法力学原理清晰，计算结果相对准确，且可靠度较高，便于工程应用。