固体推进剂捏合工序燃爆事故的模糊事故树分析

钱 辉，杨 森，刘小琴，何中其，彭琪琪

(1.江苏省特种安全防护产品质量监督检验中心,江苏 泰州 225300;2.南京理工大学化工学院,江苏 南京 210094;3.陕西应用物理化学研究所,陕西 西安 710061)

从中国古代黑火药到1896年Unge在瑞典首次制成的双基推进剂，再到二战期间Malina和von Kàrmàn发明的复合推进剂[1]，固体推进剂的研究经历了一个漫长的发展过程。此后，固体推进剂技术不断推陈出新，对人类航天事业的发展和科学技术的进步作出了巨大贡献。但由于固体推进剂自身高能量、高危险的特性，其在生产、搬运、贮存和使用过程中较易发生燃爆事故。据有关资料统计，美国生产复合推进剂的工厂在1956—1963年期间，发生混合设备着火爆炸事故多达38起[2]；日本在1935—1966年期间，至少发生14起严重的硝化棉自燃爆炸事故[3]。另据不完全统计，近年来我国发生固体推进剂重大事故300多起，导致260多人死亡、360多人中毒、180多人烧伤，有些事故甚至造成发射失败以及巨大的财产损失[4]。

为给企业的危险源监控和事故预防工作提供指导，降低事故发生率，减小事故后果损失，提高企业的安全管理水平，国内外学者对固体推进剂生产安全性问题进行了大量的研究工作。如青勤等[5]运用模糊综合分析法对引起固体推进剂生产过程中粉尘爆炸的危险性进行了综合评价；李晋等[6]针对固体推进剂压延生产中发生燃烧的影响因素进行了实验研究，并分析了固体推进剂灭火效果的影响因素;Manha[1]分析了固体推进剂系统和液体推进剂系统的主要安全隐患，并提出了在储存、搬运和运输过程中相应的安全控制措施。

本文对固体推进剂生产过程中发生燃爆事故的原因进行了分析，构建了固体推进剂捏合工序燃爆事故的事故树，并引入模糊集概念，以模糊数和模糊隶属函数计算基本事件的失效概率，用模糊概率代替基本事件的发生概率，最后依据模糊概率大小的排序，找出固体推进剂捏合工序燃爆事故防范的重点。

1 模糊事故树分析法

1. 1 事故树分析法

事故树分析(Fault Tree Analysis，FTA)法又称故障树分析法，是目前最为常见的一种逻辑较严密的安全系统工程的重要分析方法，该方法既可做定性分析也可做定量分析。但目前由于国内外缺乏关于事故树基本事件实际故障率的数据，同时运用事故树对系统进行定量评价过程中，基本事件发生的概率存在一定的模糊性，因此采用事故树对系统进行定量分析时，仅能利用各基本事件结构重要度来表征基本事件对顶上事件的影响程度或利用经验公式计算顶上事件发生的可能性，并不能对基本事件发生的概率给出明确的量化判断。此外，运用事故树对系统进行定量评价过程中经常包含不确定的信息，不能用明确的数值来表示，这时通常会出现基本事件的结构重要度相同或计算不精确的情况，致使评价结果较为宏观，无法确切地指导安全工作人员开展预防工作[7]。而模糊集理论可以处理这类由于评价对象的不确定性和模糊性引起的不精确问题[8]，因此可以考虑采用模糊数来表示基本事件发生的模糊概率。

1. 2 模糊事故分析法的基础理论

本文采用模糊数来表示基本事件发生的模糊概率。即：首先对基本事件发生频率的等级进行评价；然后运用隶属函数将基本事件发生频率的等级转化为模糊数；最后将模糊数转变为基本事件的模糊概率[9]。

1.2.1 基本事件发生频率的分级和模糊数及模糊隶属函数的计算

常用的模糊数隶属函数有三角形模糊隶属函数和梯形模糊隶属函数两种,本文将使用三角形模糊隶属函数[10]。将基本事件的发生频率用非常低、低、中等、高、非常高5个等级进行描述，相应的模糊数为[0,10,20]、[10,25,40]、[30,50,70]、[60,75,90]、[80，90，100]，基本事件不同发生频率等级对应的模糊隶属函数可分别表示如下[11]：

(1)

(2)

(3)

(4)

(5)

式中：fVL(x)、fL(x)、fM(x)、fH(x)、fVH(x)分别表示基本事件发生频率中非常低、低、中等、高、非常高5个等级的模糊隶属函数，5个模糊隶属函数的曲线见图1；x表示某个基本事件的发生频率。

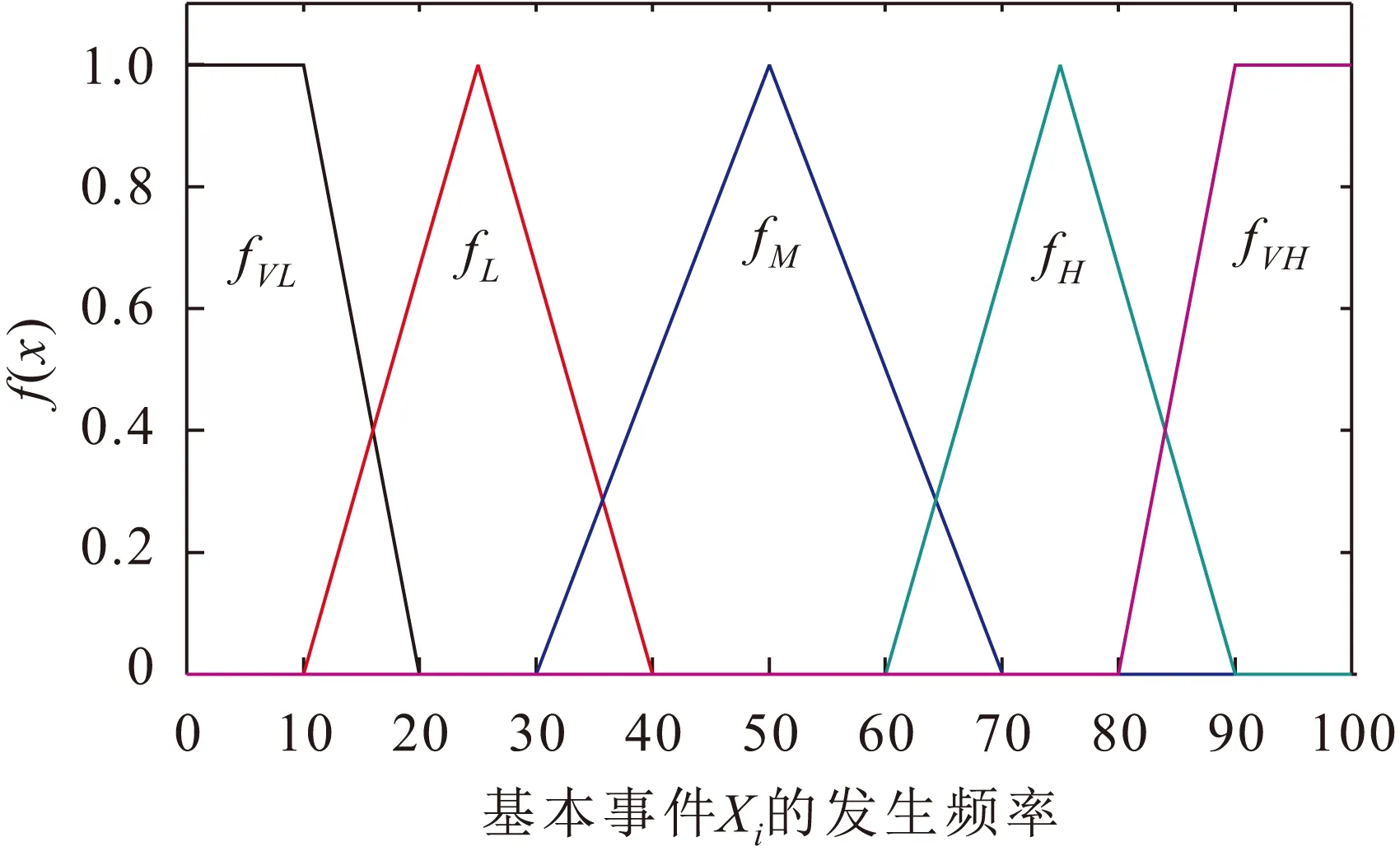
图1 基本事件发生频率等级的三角形模糊隶属函数的 曲线图[11]Fig.1 Membership function diagram of the frequency levels of basic events[11]

现假设有模糊数A和B，采用模糊集合中的截集λ可分别表示如下[12]：

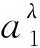
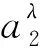
式中：a、b分别为模糊数的左、右分布参数，表示函数向左和向右延伸的程度均为小于1的正数。

因此，上述模糊数的隶属函数可用λ表示如下：

(6)

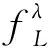
(7)

(8)

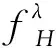
(9)

(10)

其相应的运算定义如下[11]：

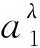
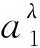
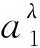
1.2.2 模糊数转化为基本事件的模糊概率[13]

不同评价人员因经验的差异，对同一基本事件发生频率的等级评价是不同的，因此需要将所有的评语进行整合[14]。本文根据邀请的评价人员的工作年限对各评价人员分配不同的权重，再同评价人员给出的模糊数进行整合，即可得到该基本事件的模糊数，其计算公式为

(11)

式中:fi表示基本事件Xi的模糊数;wj表示评价人员的权重;fij表示评价人员对基本事件Xi给出的模糊数。

根据基本事件的模糊数，即可得到该模糊数对应的模糊隶属函数，其计算公式如下[15]：

(12)

式中：FM表示模糊集合M的模糊隶属函数；yR表示函数y=0.01x与上述所求的模糊隶属函数右侧交点的y值;yL表示函数y=1-0.01x与上述所求的模糊隶属函数左侧交点的y值。

最后将模糊数转化为基本事件的模糊概率。因此基本事件的模糊概率值PM[16]可表示如下：

(13)

(14)

式中：k表示模糊概率的指数指标值;PM表示基本事件的模糊概率值。

1. 3 模糊事故树分析法的基本步骤

本文采用模糊事故树分析法对固体推进剂捏合工序燃爆事故的风险进行定量评价的基本步骤如下：

(1)通过分析固体推进剂捏合工序过程中可能导致燃爆事故发生的基本事件，建立其燃爆事故的事故树。

(2)对固体推进剂捏合工序燃爆事故的事故树进行定性分析，得到事故树的最小径集。

(3)采用专家评语的方式对基本事件发生频率进行分级，并由模糊数截集和模糊概率算法计算基本事件的模糊概率。

(4)根据各基本事件模糊概率大小的排序，找出引起燃爆事故风险的薄弱环节。

2 实例应用与分析

2. 1 建立事故树

应用事故树分析法对风险事件发生的原因逐层分解，建立风险事件的事故树。固体推进剂生产过程主要有吸收药制备、压延、捏合、压伸、烘药、切药、包装等工序，其中最易发生燃爆事故的工序是捏合工序和压伸工序，因此本文选择固体推进剂捏合工序，对该工序燃爆事故的风险进行定性和定量分析。已有研究[17]建立了固体推进剂捏合工序燃爆事故的事故树，见图2。

2. 2 定性分析

本文运用布尔代数法对建立的固体推进剂捏合工序燃爆事故的事故树进行定性分析，计算得到该事故树的最小割集和最小径集。鉴于该事故树的最小割集数较多，通过将事故树转化为成功树并计算最小径集，得到该事故树的最小径集如下：

P1={X1,X2,X3}

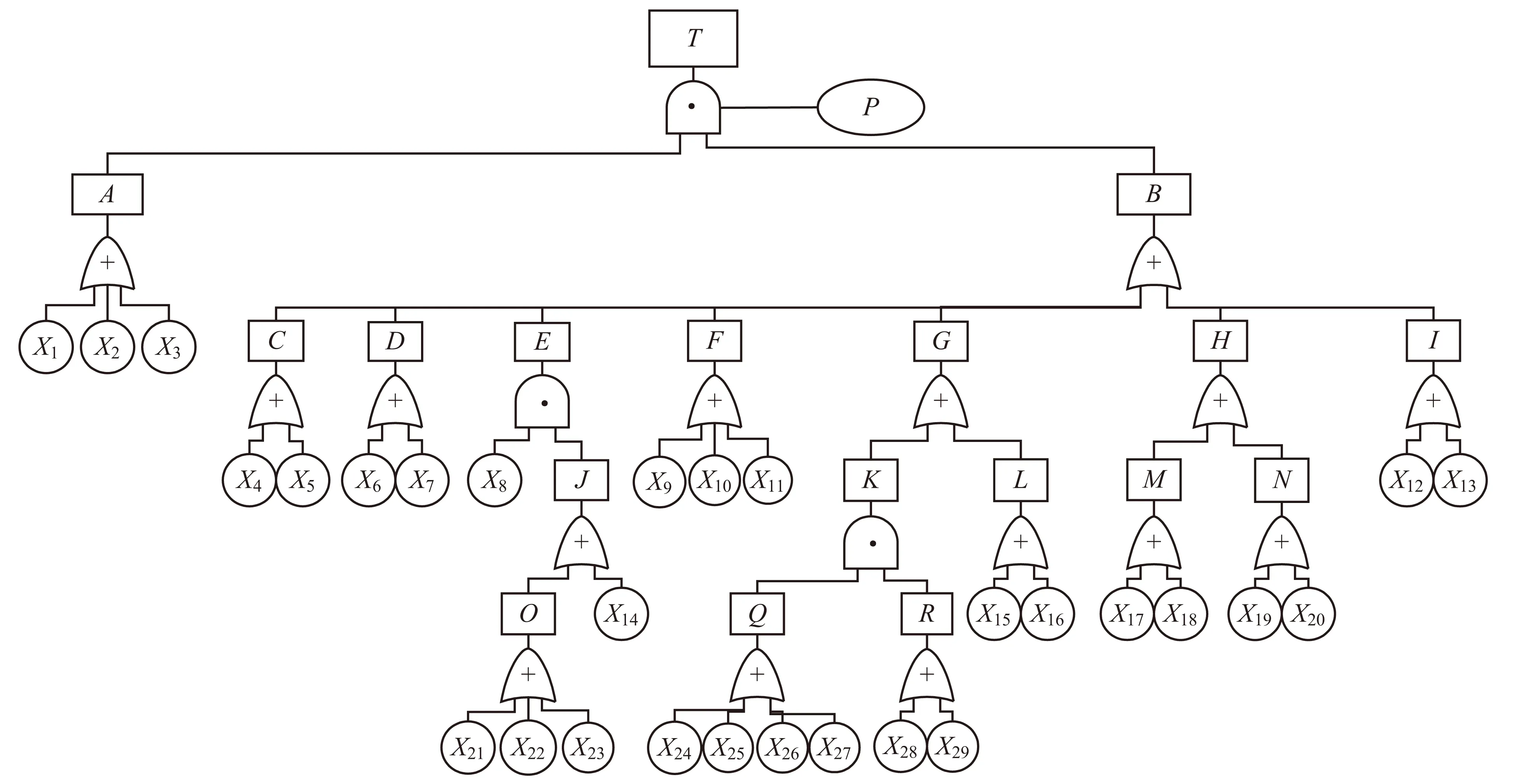
图2 固体推进剂捏合工序燃爆事故的事故树[17]Fig.2 Fault tree of the blast accidents in kneading process of solid propellants[17]T.固体推进剂捏合工序燃爆事故；P.爆炸极限；A.药料异常；B.点火源；C.明火；D.电火花；E.雷击火花；F.撞击；G.静电；H.摩擦；I.高温；J.避雷失效；K.机体静电；L.人体静电；M.物料之间摩擦；N.物料与机体摩擦；O.避雷设备故障；Q.静电积累；R.静电接地；X1.热分解产生气泡；X2.混入硬性杂质；X3.含水率过低；X4.工房内吸烟；X5.工房内违章动火；X6.使用电子通讯设备；X7.未使用防爆电具；X8.雷击；X9.药缸撞击；X10.使用铁质工具作业；X11.穿带铁钉的鞋作业；X12.工房内温度过高；X13.保温水温度过高；X14.未安装避雷设备；X15.未穿防静电工作服；X16.进工房前未消除静电；X17.药料黏度过低；X18.药料颗粒度不均匀；X19.桨叶转矩过大；X20.桨叶转速过快；X21.接地电阻超标；X22.引下线损坏；X23.接地端损坏；X24.药料导电率过低；X25.药料投放速率过快；X26.药缸内有磨损或焊疤；X27.接口处不平整；X28.未设置接地设施；X29.接地端损坏

事故树最小割集表征的是系统危险性，即最小割集越多，系统危险性越大；事故树最小径集表征的是系统安全性，即最小径集越多，系统安全性越高。由上述事故树计算得到的最小割集数为81，最小径集数为5，因此该捏合工序燃爆的危险性很高。

2. 3 定量分析

2.3.1 基本事件的评价等级

上述事故树的基本事件包含有二值基本事件、随机基本事件和条件事件。二值基本事件是指事件发生时P=1，事件不发生时P=0，X7、X14、X15、X16、X21、X28都属于二值基本事件；P为条件事件；其余基本事件均为随机基本事件。

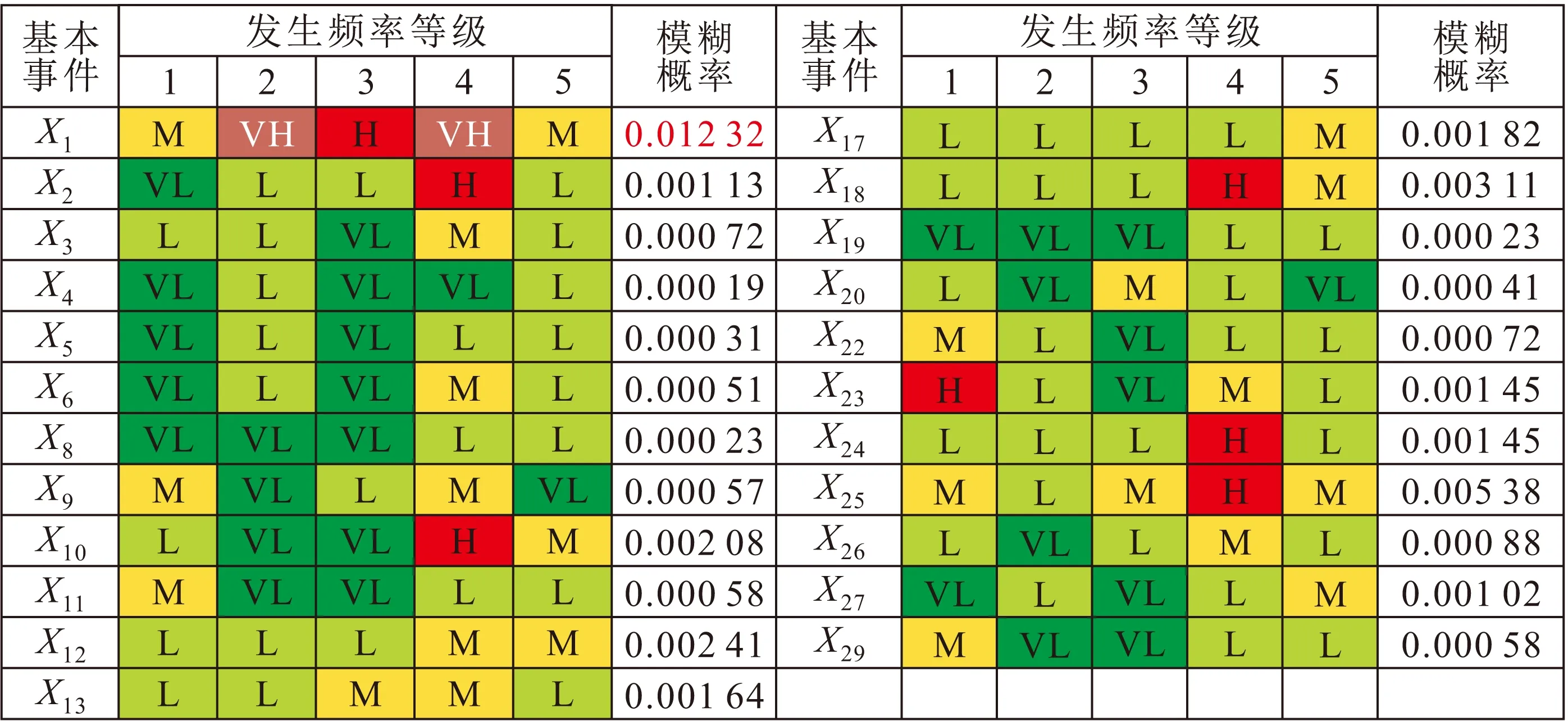
由于缺少基本事件发生概率的数据，在没有试验验证的情况下，可以根据以往事故的统计数据以及评价人员的经验，将随机基本事件的发生频率用非常低、低、中等、高、非常高5个等级进行描述。本研究中由3位专业评价人员和2位安全工作人员给出各随机基本事件发生频率的等级，详见表1。

2.3.2 确定各随机基本事件的模糊概率值并排序

根据表1中随机基本事件发生频率的等级计算随机基本事件的发生概率。本文根据邀请的评价人员的工作年限对各评价人员分配不同的权重，这5位评价人员所代表的权重值为w=(0.150 0，0.100 0，0.200 0，0.150 0，0.400 0)。

由于篇幅所限，本文以随机基本事件X1为例，其中这5位评价人员给出的随机基本事件发生频率的等级分别为中等、非常高、高、非常高、中等，根据公式(6)～(11)，可计算得到随机基本事件X1的模糊数为

表1随机基本事件发生频率的等级表

Table 1 Frequency level of random basic events

f1=(w1+w5)fM+(w2+w4)fVH+w3fH=(0.400 0+0.150 0)[(30+20λ),(70-20λ)]+(0.100 0+0.150 0)[(180+10λ),100]+0.200 0[(60+15λ),(90-15λ)]

=[(48.5+16.5λ),(81.5-14λ)]

该随机基本事件X1对应的模糊隶属函数为

联立公式计算yR和yL,有:

再由公式(12)～(14)，可计算得到随机基本事件X1的模糊概率值，即

PM1=10-k=0.012 32

该随机基本事件X1的模糊概率值为0.012 32。同样，可计算得到其他随机基本事件的模糊概率值(见表1)，因此各随机基本事件模糊概率值大小的排序为:X1>X25>X18>X12>X10>X17>X13>X23=X24>X2>X27>X26>X3=X22>X11>X29>X9>X6>X20>X5>X8>X19>X4。

即表明随机基本事件X1、X25、X18、X12、X10发生的可能性最大，同时也是该捏合工序中最为薄弱的环节，其分别表示的是热分解产生气泡、药料投放速率过快、药粒颗粒度不均匀、工房内温度过高和使用铁制工具作业。通过对比分析发现随机基本事件——热分解产生气泡发生的模糊概率最大，同时其结构重要度[16]也最大，说明该随机基本事件对固体推进剂捏合工序发生燃爆事故的影响重大。

3 结论与建议

本文采用模糊事故树分析法对固体推进剂捏合工序燃爆事故的风险进行了定性和定量分析，得到如下结论：

(1) 与经典的事故树分析法相比，模糊事故树分析法更为灵活，能在一定程度上反映基本事件发生概率自身的模糊性；同时利用该方法对固体推进剂捏合工序燃爆事故的风险进行定性和定量分析，可通过计算随机基本事件模糊概率的大小，找出引起燃爆事故的薄弱环节，快速确定危险预防的重点，可为降低固体推进剂生产过程中发生燃爆事故提供理论基础。

(2) 利用模糊事故树分析法对固体推进剂捏合工序燃爆事故的风险进行了定量分析，结果发现在固体推进剂捏合工序中热分解产生气泡、药料投放速率过快、药粒颗粒度不均匀、工房内温度过高和使用铁制工具作业最容易造成爆燃事故，因此在设计、试运行、投产运行过程中要对这些危险因素加以消除或控制，以实现过程的本质安全。

(3) 由于该方法是在评价人员评语的基础上计算得到的各随机基本事件的模糊概率，因此其对各随机基本事件描述的精确度受评价人员主观经验的影响，因此建议应尽可能地使样本足够大并选取经验丰富的人员成立评价专家组，以得到更准确的评价结果。