武汉市地铁网络复杂特性与鲁棒性研究

甘俊杰，聂规划，徐 迪

(武汉理工大学经济学院，湖北 武汉 430070)

随着我国经济的快速发展，城市人口急速上升，在我国城市化进程脚步加快的背景下，我国大城市道路交通拥堵的现象日益严重。为了降低城市路面交通的负荷量，城市地铁因其污染小、载客量大、安全系数高等优势，逐渐成为各大城市及国家关注的热点[1]。从1969年我国第一条地铁线建成运营，至2016年末，我国累计30个城市建成投运地铁线路共计134条，其中上海、北京、广州等一线城市均已建成相当规模的地铁网络。武汉市作为我国中心城市之一，在经济快速发展的同时，轨道交通同样发展迅速。截至2016年12月28日，武汉市已投入运营地铁线路5条共123座车站，运营规模直追北上广等一线城市。

近年来随着对“复杂网络”研究的发展，国际上掀起了一轮利用复杂网络理论研究现实网络的热潮。复杂网络理论兴起于20世纪60年代，其不仅能够用以研究现实网络的几何性质，更能用以研究显示网络的形成机制与演化规律等[2]。武汉市地铁网作为一种典型的现实网络，基于复杂网络理论对其进行特性分析，能够直观地反映地铁网络的各项结构特征，为武汉市地铁的规划建设提供理论依据与政策建议。

国内外学者对复杂网络及地铁网络的复杂特性均有了初步的研究。在国外，Watts等[3]为了描述从一个局部有序系统到随机网络的转移过程，提出了小世界网络模型(WS);Latora等[4]研究了波士顿地铁网络的特性，并创造性地提出了网络构造规则；Seaton等[5]对比分析了维也纳和波士顿地铁网络，指出地铁网络具有聚类系数高和路径长度短的特点，呈现出小世界网络的特征。在国内，丁益民等[6]对我国北京、上海、广州等城市的地铁网络进行了实证研究，并提出了一种基于社团结构的城市地铁网络模型，该模型很好地解释了我国各城市交通运输网的网络特性；张晋等[7]基于复杂网络理论和平面图理论，针对北京市地铁实际网络及运营关系，分别构建了Space-L和Space-P拓扑结构模型，通过计算模型的统计特征指标，得出北京市地铁网络具有小世界性和无标度性；王燚等[8]、慈立坤等[9]利用复杂网络理论研究了上海等大城市地铁网络的结构复杂性和结构脆弱性。

中国城市地铁建设发展飞快，武汉市地铁发展速度尤为惊人，但目前对我国城市地铁网络的研究多集中于北京、上海等大型城市，对于武汉这样的中心城市尚缺乏研究。因此，本文以武汉市地铁网络系统为例进行了实证研究，通过运用复杂网络理论和方法构建了武汉市地铁网络的Space-L和Scape-P网络拓扑结构模型，分析了武汉市地铁网络的复杂特性，并对武汉市地铁网络的鲁棒性进行了研究。该研究成果可为武汉市地铁网络的日常维护及安全运营提供合理的建议。

1 武汉市地铁网络及统计参量

网络图是用来构建并分析现实网络的基础研究方法，一个具体的现实网络可利用图论方法抽象为一个由点集V和边集E组成的一个对，一般表述为图G=(V,E)。本文通过定义地铁网的拓扑结构来研究实际的地铁网络。将地铁站点定义为节点，站点间的相互联系定义为连边，但根据节点连接关系的不同表述，建立实际地铁网络模型和复杂网络模型的方法常分为Space-L网络拓扑结构模型和Space-P网络拓扑结构模型。在Space-L网络拓扑结构模型中，点集代表站台集合，若站台i和站台j是相邻站台，则节点i和节点j之间存在连边；与之不同的是，在Space-P模型中，若站台i和站台j是处于同一地铁线路中，则节点i和节点j之间存在连边。

图1给出了两种不同网络拓扑结构模型(Space-L网络拓扑结构模型和Space-P网络拓扑结构模型)表示的一个简单的地铁网络，分别用数字1,2,…,9对站点进行编号。该地铁网络实际包含两条地铁线路，编号1～5的节点构成线路1，节点3及节点6～9构成线路2。图1(a)中，Space-L网络拓扑结构模型很好地还原了实际地铁网络的地理结构，保留了地铁网络的基本网络特性；图1(b)中Space-P网络拓扑结构模型则很好地反映了地铁网络的换乘状况。

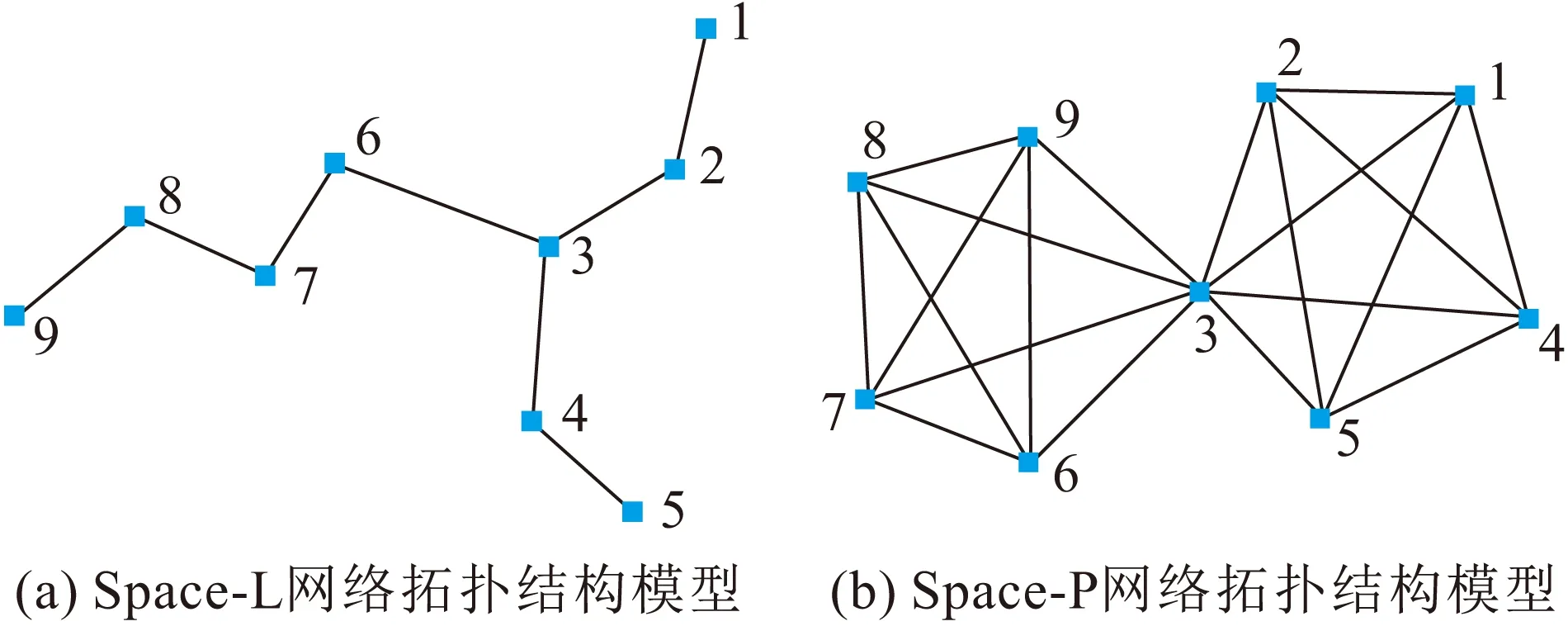
图1 地铁网络的拓扑结构模型Fig.1 Topological structure models of metro network

由图1可见，城市地铁网络由一系列节点与节点间的连边组成，因此常引入一些统计变量用以描述地铁网络的复杂特性。本文对地铁网络的复杂特性描述如下[10]：

(2) 节点的聚类系数。节点的聚类系数Ci是用来衡量网络节点分布的密集程度的物理量，其定义为节点i的所有邻接节点之间实际存在的连边数目Ei除以可能的最大连边数目，即Ci=2Ei/[ki·(ki-1)]。在交通运输网络中，节点的聚类系数反映了网络站点分布的疏密程度。

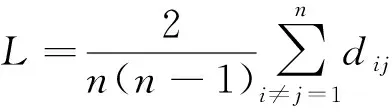
2 武汉市地铁网络的复杂特性分析

本文选取武汉市2017年底地铁规划线路图(见图2)进行实证分析。结合武汉市地铁实际网络，利用图论思想构建地铁网络的邻接矩阵，并利用Ucinet 6.2版本软件分别构建了Space-L网络拓扑结构模型和Space-P网络拓扑结构模型，对武汉市地铁网络的复杂网络特性进行分析。统计发现：在2017版武汉市规划的地铁网络中，共有7条地铁线路148个站点。

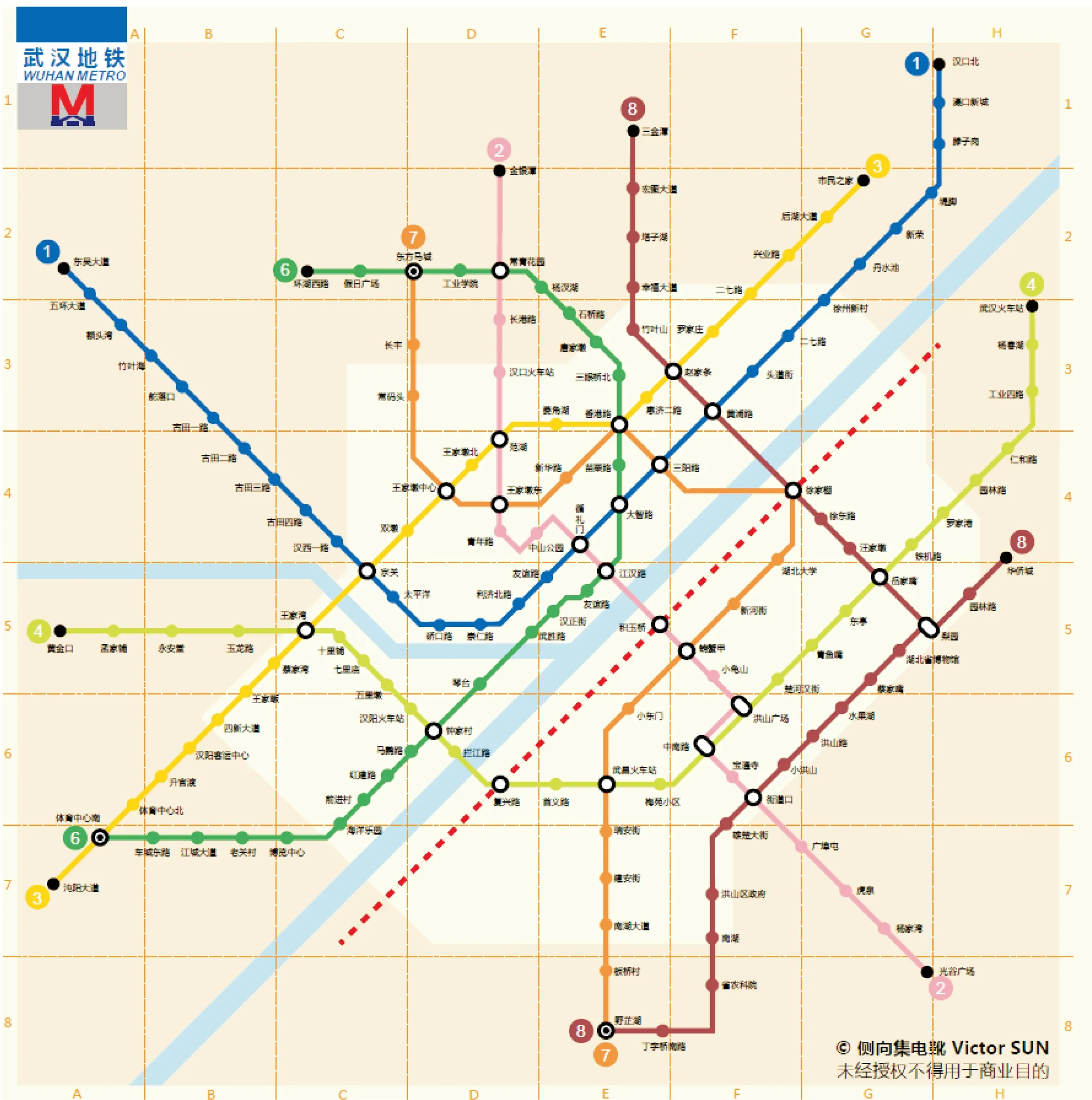
图2 武汉市2017年底地铁规划线路图(数据来源：武汉市地铁网)Fig.2 Metro planning line map of Wuhan City at the end of 2017

2.1 Space-L网络拓扑结构模型分析

2.1.1 节点的度与度分布

在Ucinet软件中沿路径Network—Centrality—Degree得到网络节点的度值，利用Origin进行数据处理并作图，得到Space-L网络拓扑结构模型中武汉市地铁网络节点的度与度分布，见图3。

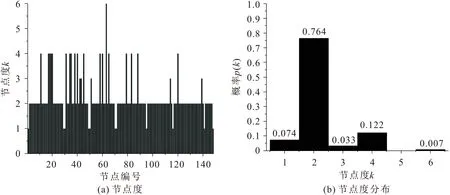
图3 Space-L网络拓扑结构模型中武汉市地铁网络节点的度与度分布Fig.3 Node degree and node distribution of Wuhan metro network based on Space-L network topological structure model

由图3可见，武汉市地铁网络节点度的最大值为6，最小值为1(各线路起始站)，而网络节点度的平均值为2.23；节点度为2的站点占比76.4%，说明武汉市地铁网络中大部分站点只与同线路中的两个相邻站点具有连接关系。

2.1.2 节点的聚类系数

上述分析结果表明大部分节点的度值为2，说明在武汉市地铁网络中大部分节点只与同线路的2个节点建立连接，因此在Space-L网络拓扑结构模型中节点间表现出很微弱的集聚性。沿路径Network—Cohesion—Clustering coefficient计算各节点的聚类系数C并绘制散点图，见图4。

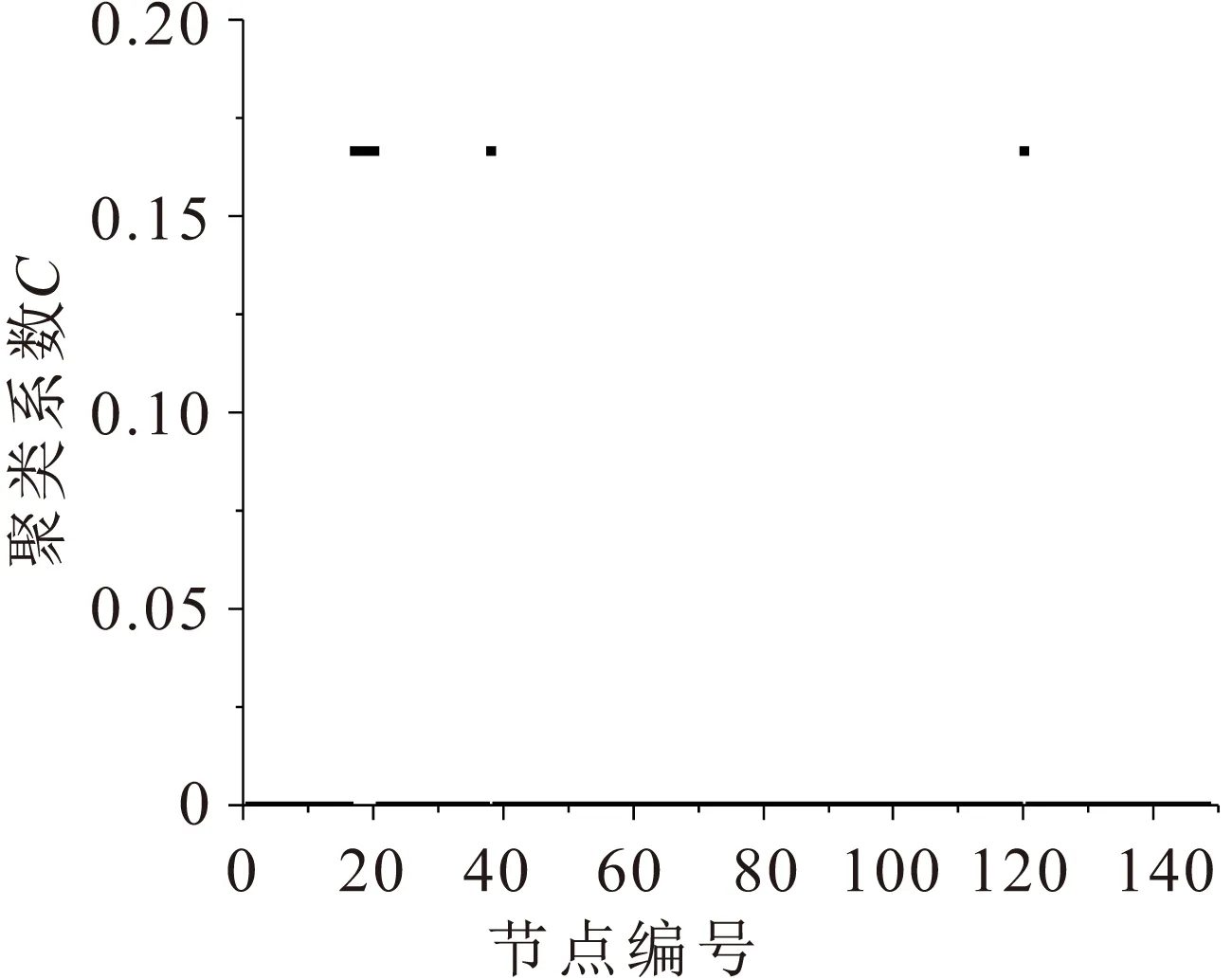
图4 Space-L网络拓扑结构模型中武汉市地铁网络 节点的聚类系数散点图Fig.4 Scatter plot of the node clustering coefficient of Wuhan metro network based on Space-L network topological structure model

由图4可见，除17、18、19、20、38、120号节点具有较小的聚类系数(C=0.167)外，其余各节点的聚类系数均为0，武汉市地铁网络节点的平均聚类系数为0.007。

2.1.3 节点间的最短路径长度

沿操作路径Cohesion—Distance计算节点间最短路径长度L的概率分布和累计概率分布并绘图,见图5。

图5 Space-L网络拓扑结构模型中的武汉市地铁网络 节点间最短路径长度的概率分布和累计概率分布Fig.5 Probability distribution and cumulative probability distribution of the shortest path length between the nodes of Wuhan metro network based on Space-L network topological structure model

由图5可见，武汉市地铁网络节点间最短路径长度L的概率分布图形拟合为一个非对称的单值函数，各节点间最短路径长度的最大值为28，大部分节点间的最短路径长度为10，这意味着大部分站点间的可达距离为10站，网络的平均最短路径长度为10.617[见图5(a)]；约50%节点间的最短路径长度小于10，约90%节点间的最短路径长度小于15[见图5(b)]，说明在武汉市乘坐地铁具有很高的出行效率。

2.2 Space-P网络拓扑结构模型分析

2.2.1 节点的度与度分布

由于同一线路的节点彼此相连，因此Space-P网络拓扑结构模型中的节点比Space-L网络拓扑结构模型中的节点拥有更大的节点度。本文利用第2.1.1节中节点度计算路径的相同方法分析，得到Space-P网络拓扑结构模型中节点度的最大值为55，最小值为11，而网络节点度的平均值为25.70。由于节点度值的差异较大，因此本文采用累积分布函数研究节点的度分布，即在双对数坐标下对节点的累计度分布进行图像拟合，其拟合结果见图6。

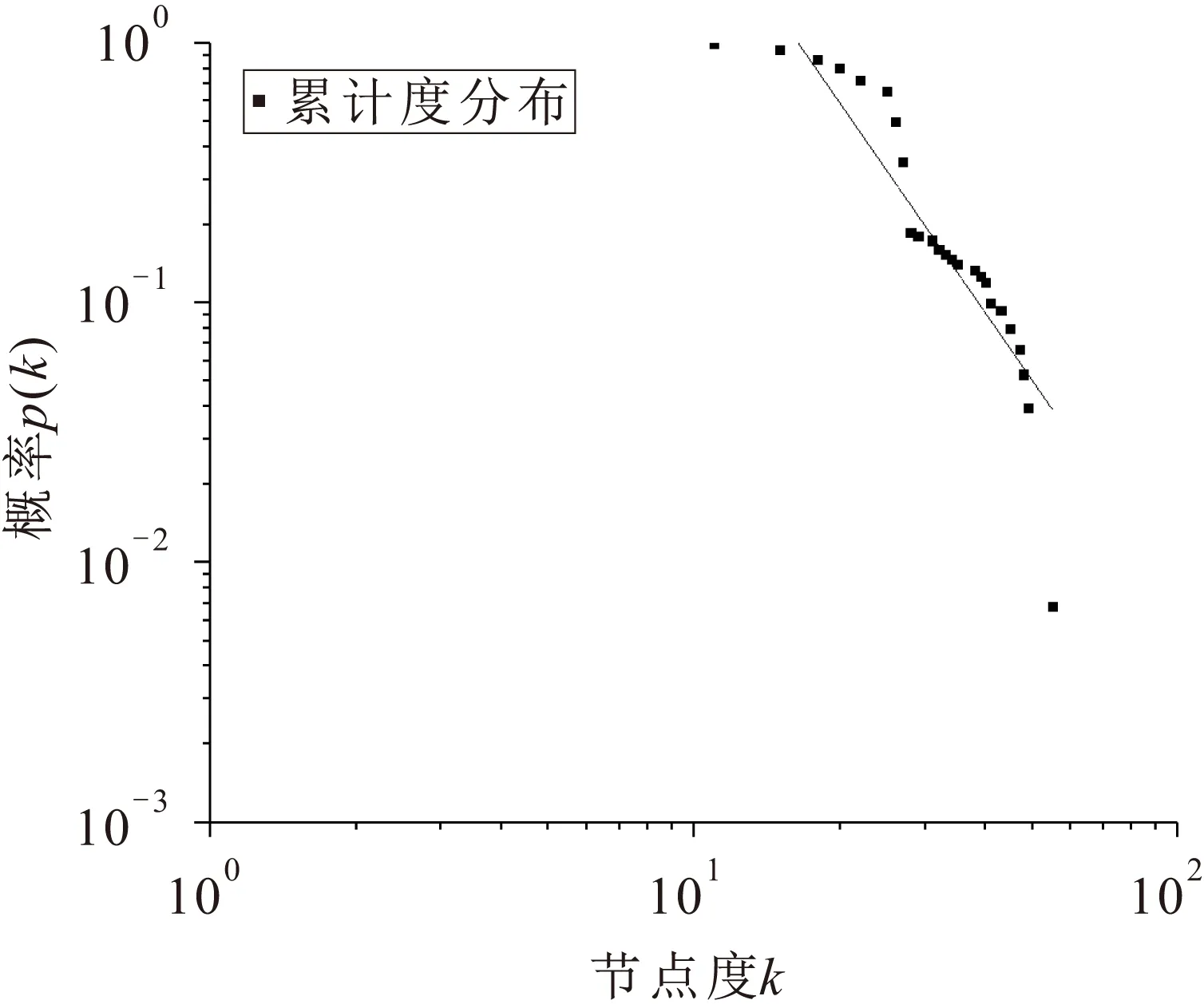
图6 双对数坐标下Space-P网络拓扑结构模型中 武汉市地铁网络节点的累计度分布Fig.6 Cumulative distribution of node degree of Wuhan metro network based on Space-L network topological structure model in double logarithmic coordinates

由图6可见，在Space-P网络拓扑结构模型下的武汉市地铁网络具有无标度网络的特性。分析原因认为：不同地铁站由于其所处地理位置的不同，一些处于最佳商业位置的地铁站点会拥有更大的可能性连接其他节点，因此导致节点度的幂率分布。

2.2.2 节点的集聚系数

与Space-L网络拓扑结构模型不同，Space-P网络拓扑结构模型中的节点表现出非常高的密集度。图7为Space-P网络拓扑结构模型中武汉市地铁网络节点的集聚系数C。

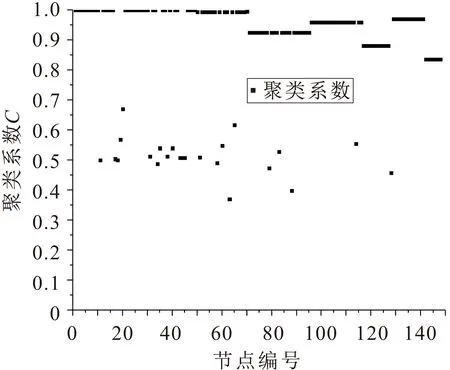
图7 Space-P网络拓扑结构模型中武汉市地铁 网络节点的聚类系数CFig.7 Clustering coefficient of nodes C of Wuhan metro network based on Space-L network topological structure model

由图7可见，约72.3%的节点拥有0.9以上的集聚系数，而网络节点的平均集聚系数为0.883。分析原因认为：在Space-P网络拓扑结构模型中由于绝大部分站点只属于一条线路，这样的站点只与该线路上的其他节点相连，因此表现出节点的集聚系数接近于1的特性。

2.2.3 节点间的最短路径长度

在Space-P网络拓扑结构模型中，节点i与节点j之间的最短路径长度dij用来表示两站点间的换乘次数，即换乘次数=dij-1。图8为Space-P网络拓扑结构模型中武汉市地铁网络节点间最短路径长度的概率分布。

图8 Space-P网络拓扑结构模型中武汉市地铁网络 节点间最短路径长度的概率分布Fig.8 Probability distribution of the shortest path length between the nodes of Wuhan metro network based on Space-L network topological structure model

由图8可见，武汉市地铁网络各节点间最短路径长度的最大值为3，说明从任意一个站点到其他任何站点最多需要换乘2次；网络中约66%的节点间的最短路径长度为2，节点间的平均最短路径长度为1.99，表明在武汉市乘坐地铁一般只需要换乘1次即可，这体现了武汉市地铁出行的高效性。

3 武汉市地铁网络的鲁棒性分析

3. 1 地铁网络鲁棒性的评价指标

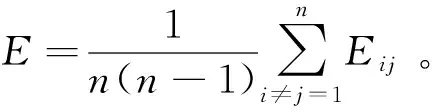
式中:G为网络最大连通子图节点比例；N′为遭受破坏后的网络包含的最大连通分支中的节点数；N为全局网络的节点数。

3.2 地铁网络随机故障和蓄意攻击两种策略

地铁网络遭受的故障可能包括自然环境灾难、机器故障或信号问题等，遭受的攻击可能包括恶意攻击和恐怖袭击。故障具有随机性，而攻击则包含很强的目的性，为造成最大的攻击效果，一般会选择攻击网络中的重要节点。为了更好地还原实际地铁网络的拓扑结构，本文以武汉市地铁网络为例，采用Space-L网络拓扑结构模型对武汉市地铁网络在遭受随机故障和蓄意攻击后的网络拓扑结构进行了仿真模拟。在本次仿真模拟过程中，通过MATLAB产生随机数的方式模拟站点故障，通过去除最高节点度值的节点用以模拟蓄意攻击，同等度值的节点同样通过随机数的方式进行选择性剔除。为了避免仿真模拟结果产生较大的偏差，本次在同等条件下进行5次仿真模拟试验，并对每次试验后的网络最大连通子图节点比例Gi取平均值,以得到最后的G值。最后模拟得到武汉市地铁网络在遭受随机故障和蓄意攻击两种情况下，模拟节点3失效后网络拓扑结构的仿真结果，见图9。

图9 武汉市地铁网络遭受随机故障和蓄意攻击后的 网络拓扑结构示意图Fig.9 Schematic diagram of the network topology of Wuhan metro network after random failure and deliberate attack

3.3 节点失效策略下地铁网络连接效率的仿真试验

依照前述提出的衡量地铁网络鲁棒性的指标以及相应的仿真模拟策略，本文基于Space-L网络拓扑结构模型对武汉市地铁网络在遭受随机故障和蓄意攻击后的连接效率进行了仿真试验，以检测地铁网络的鲁棒性。通过MATLAB仿真模拟并计算得到武汉市地铁网络在遭受随机故障和蓄意攻击时网络最大连通子图节点比例G(即网络连接效率)的变化曲线，见图10。

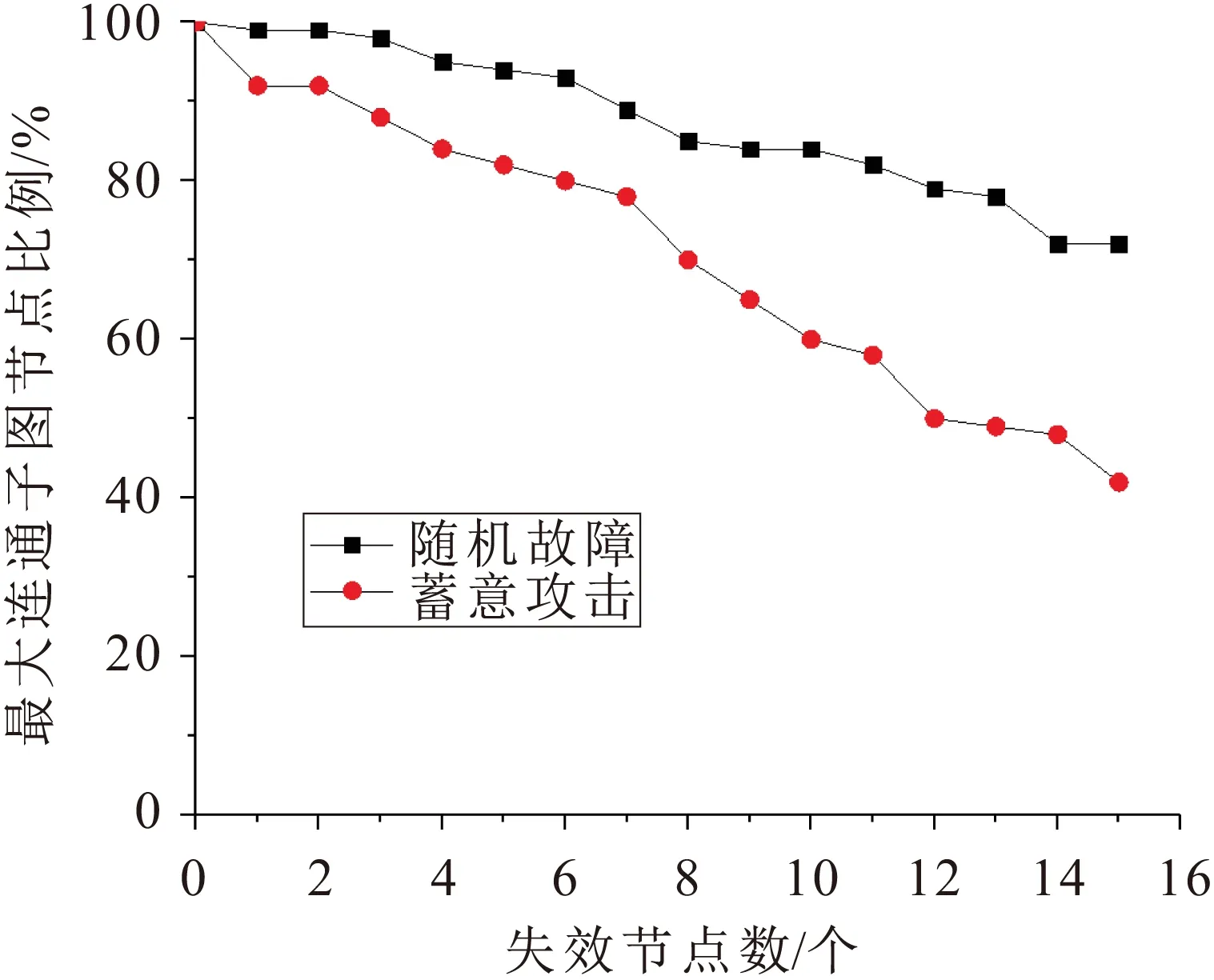
图10 节点失效策略下武汉市地铁网络连接效率的 变化曲线Fig.10 Curves of the link efficiency of Wuhan metro network under node failure strategy

由图10可见，当武汉市地铁网络站台节点遭受随机故障时，15个节点连接失效将导致全局网络最大连通子图节点比例下降到72%，网络整体失效率为28%，单个节点失效平均造成全局网络失效率达1.87%，即表明在武汉市地铁网络中，当有10%度数大的站点遭遇随机故障而停止运营时，网络全局效率为无站点故障时的72%。以上仿真模拟试验数据表明：武汉市地铁网络具有较好的鲁棒性，能够有效应对可能出现的站点随机故障问题。这是因为在武汉市地铁网络中，度数为2的节点占比达76.4%，这意味着在随机选择故障节点时，有极大的概率选中这些度数为2的节点，而这些节点失效对网络全局效率的影响非常有限。

此外，由图10还可见，当武汉市地铁网络站台节点遭受蓄意攻击时，15个节点连接失效直接导致全局网络最大连通子图节点比例下降到42%，网络整体失效率高达58%，单个节点失效平均造成全局网络失效率高达3.87%，为随机故障时的2.07倍，即表明在武汉市地铁网络中，当有10%度数大的站点遭受蓄意攻击而停止运营时，网络全局效率仅为无站点遭受攻击时的42%，此时整个地铁网络几近瘫痪。这是因为当人为蓄意攻击地铁站点时，攻击者往往会选择攻击度数较大的节点，而这些节点一般处于地铁网络的中心位置，节点失效会造成多条通过该节点的线路失效，从而严重影响地铁网络的连通性。

通过对上述仿真试验结果分析可知，武汉市地铁网络对随机故障具有较好的鲁棒性，但是对可能遭受的蓄意攻击表现出脆弱性，这是无标度网络鲁棒性的体现。因此，对于地铁网络的管理者而言，对地铁网络中度数较大的站点应加强巡视与安检力度，以最大限度地保证整个地铁网络畅通运行，从而提高服务效率。本文列出了武汉市地铁网络中节点度值排名前15位的站点，详见表1。

由表1可知，归属地铁线路1、2、3、6号线的站点数均为5个，归属地铁线路4、7号线的站点数为4个，归属地铁线路8号线的站点数为3个，说明在武汉市地铁网络中，1、2、3、6号线承担着主要的换乘任务，共计覆盖的换乘站点数达到88%，体现出这些站点在地铁网络中的重要性。

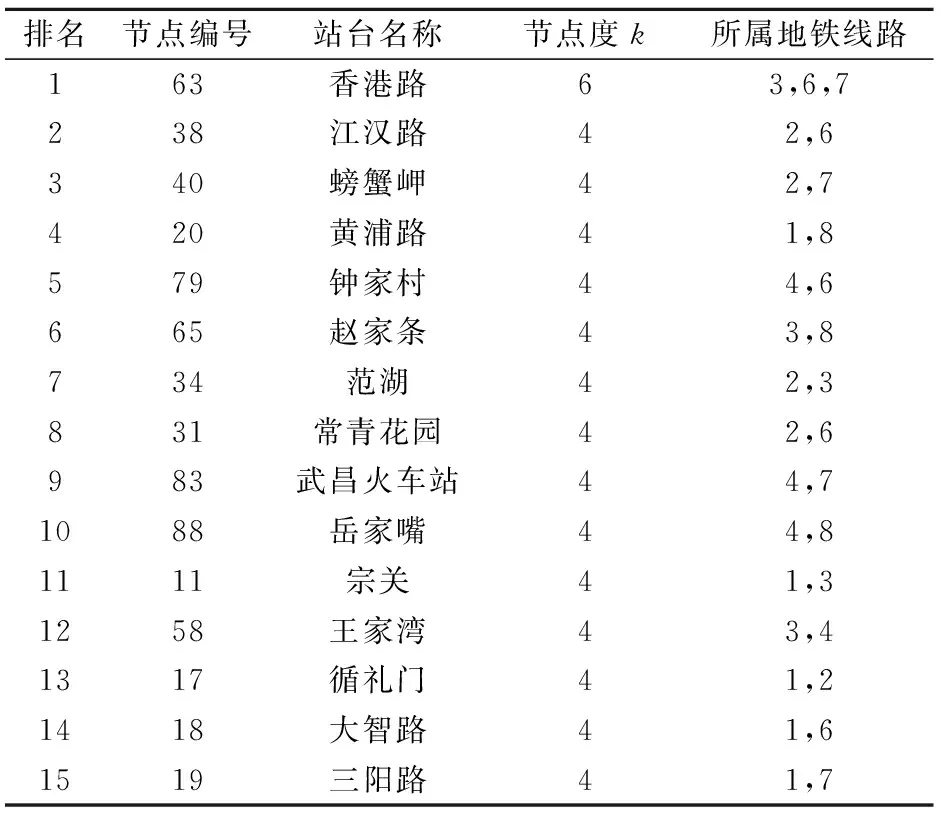
表1 武汉市地铁网络中节点度值排名前15位的站点

4 结 论

本文对武汉市地铁网络进行了实证研究。首先利用复杂网络理论分别构建了武汉市地铁网络的Space-P和Space-L网络拓扑结构模型，并分别对其进行了复杂网络特性分析；然后研究了武汉市地铁网络的鲁棒性，通过制定武汉市地铁网络随机故障和蓄意攻击两种策略，基于Space-L网络拓扑结构模型对武汉市地铁网络在遭受随机故障和蓄意攻击后的连接效率进行了仿真试验，以检测武汉市地铁网络的鲁棒性。得到的主要结论如下：

(1) 通过对武汉市地铁网络的Space-L网络拓扑结构模型进行复杂网络特性分析，结果表明：网络中76.4%的节点度为2，说明绝大多数站点只与前后两个站点相连；网络的平均最短路径长度为10.617，说明网络节点中地铁站间的平均可达站台数为10，即居民出行平均乘坐地铁站点数为10个；90%节点间最短路径长度小于15，最大节点间距离为28，这表明乘坐武汉市地铁出行的高效性。

(2) 通过对武汉市地铁网络的Space-P网络拓扑结构模型进行复杂网络特性分析，结果表明：网络节点度服从幂率分布，说明武汉市地铁网络具有无标度性；网络节点间最短路径长度平均值为2，说明武汉市居民乘坐地铁出行时，从起点到终点一般只用换乘1次，这再次验证了武汉市地铁网络运行的高效性与设计的科学性。

(3) 对武汉市地铁网络中的站点分别采用随机故障和蓄意攻击两种方式使其失效，以仿真试验检验武汉市地铁网络的鲁棒性。结果表明：武汉市地铁网络在遭遇站点随机故障时，具有很好的鲁棒性；而以最大度节点作为蓄意攻击目标时，网络表现出脆弱性，且度值越大的节点失效造成全局网络效率下降越快，当较多度值大的节点实效后，整个网络将几近瘫痪。对武汉市地铁网络鲁棒性进行仿真模拟的实际意义在于：地铁管理者应加强对节点度值较高站台的日常维护与安全检查，以保障重要节点的正常运行，防止造成地铁网络大面积的瘫痪。