比“练”更重要的是“思”——以“解决问题之取商的近似值”练习课教学为例

□ 吴国强

人教版教材五年级上册练习九“解决问题之取商的近似值”是一节练习课。一直以来，在练习课教学中，我们力求通过大量训练让学生巩固、运用知识，却疏于培养学生发现问题、提出问题和思考问题的能力。而《义务教育数学课程标准（2011年版）》提出：培养学生发现和提出问题的能力、分析和解决问题的能力是数学教学的核心目标之一。

在“解决问题之取商的近似值”练习课之前，教材安排了例6、例10对“四舍五入法”“进一法”“去尾法”三种取商近似数的方法进行系统学习。但在教学实践中我们发现，学生在解决需要对计算结果取近似值的相关问题时，正确列式没有困难。可是在具体计算时，往往会出现以下两种情况：要么一直往下除，要么问“除不尽怎么办”。显然在学习了取商近似值的各种方法后，学生对于在什么时候需要取商的近似数比较模糊。可见，这节练习课需要解决以下两大问题：一是会对计算结果需不需要取商的近似数作出正确判断；二是如果商需要取近似值，应该用哪种取值方法比较合理？重点是培养学生会根据实际情况正确判别取商近似数的意识问题。基于这样的认识，笔者在教学“解决问题之取商的近似值”一课时，尝试从学生自主生成问题入手，以“思”引领“练”为主线，突出对学生问题意识和良好思维品质的培养。

一、学有效度，在感悟中生成问题

解决问题的愿望，是学生对学习产生需求的驱动力。问题从哪里来？课前我们通过调查发现，在解决问题时，学生对于计算结果是否需要处理意识淡薄，而告诉具体取值要求后进行计算根本没有问题。针对这种现状，笔者在教学时并没有让学生列举生活中的事例，逐一练习讲解取商近似数的三种方法，而是直接改编教材练习九的第8题、整合第7题，把需要用“四舍五入法”“进一法”“去尾法”三种取商近似数的方法解决的问题整体呈现，在取舍数学信息的过程中，让学生自己去发现问题、生成问题，并在计算中体验、在思考中感悟。

【教学片段】

创设情境：节日期间老师去葡萄园参观，收集到一些数学信息。

1.在信息中生成数学问题

师：看了这些信息，你能提出一些数学问题吗？

生：照这样计算，买1千克葡萄需要多少元？

生：总价÷数量=单价。（6.3÷0.8）

生：需要准备多少个纸箱？

生：就是求600千克里有几个9.5千克？（600÷9.5）

生：宋叔叔可以进多少箱葡萄？

生：就是求1320元里有几个48元？（1320÷48）

2.在计算中生成数学问题

师：看了这些同学的解答过程，你有问题要问吗？

生：在计算时，除不尽怎么办？

生：题目中没有让我们取商的近似值，为什么要取商的近似值？

生：第2、3两题在计算时为什么不继续往下除了？

人教版教材编排的练习，既提示了数学知识点的要求和方法，又发挥了训练、迁移的作用。改编教材第41页第8题，整合练习内容，引导学生经历发现问题、提出问题的过程。“照这样计算，买1千克葡萄需要多少元？”“需要准备多少个纸箱？”“宋叔叔可以进多少箱葡萄？”这些学习材料的生成，极大地满足了不同学习水平学生的需要，起点低，每个人都能计算，又能体现出层次性，要在短时间内正确计算出三个问题的结果，具有一定的挑战性，利于挖掘学生的内在学习潜能。这样的处理，直奔练习重点，用充足的时间落实课时目标。

二、导有深度，在思辨中达成共识

练习课教学中，如果教师只关注学生的解题方法和结果是否正确，仅停留于就题解题的层面，就缺乏思维层面的反思、比较与提升。因此，在练习课教学中，当学生积累一定的解决问题的经验后，教师应及时引导学生进行回顾与反思，把解决问题的过程与方法作为研究对象进行思维的碰撞，提升解决问题的能力。依据本课时练习的重点和学生的疑难之处，适时提出“对比一下方法和计算结果，有相同的地方吗？有不同的地方吗？”引导学生进行思辨、交流。一方面作求同分析：解决这类问题要用除法、计算结果都适合用近似数表示；另一方面作求异思维，虽然解决此类问题的计算结果都适合用近似数表示，但取商近似数的方法各不相同。有时要用“四舍五入法”取商的近似数，但有时却不适合用“四舍五入法”取商的近似数，要用到“去尾法”或“进一法”。

【教学片段】

师：题目中没有让我们取商的近似值，为什么要取商的近似值？

生：因为生活中算价格最多精确到分，所以结果最多只保留两位小数。

师：也就是说联系生活实际情况，求”葡萄的单价”计算结果需要取商的近似数。

师：用什么方法取商的近似值比较合理？（板书：四舍五入法）7.88元是怎么得到的？

生：7.875保留两位小数就是7.88。

师:如果保留一位小数呢？保留到整数呢？

生：7.9元。

生：8元。

师：假如你是葡萄园老板，会取哪个值？为什么？

生：8元，赚的钱比较多。（生笑）

师：我们一起来比较一下，7.88元和8元，1千克相差多少元？10千克呢？100千克呢？1000千克？10000千克？

师：在计算2、3两题时为什么不继续往下除了？

生：生活中箱子是取整数个的，这里计算结果也需要取商的近似数。

师：既然箱子是取整数个的，用四舍五入法取商的近似值合理吗？

生：不合理，如果取63箱，剩下的1.5千克葡萄就没箱子装了。

生：只要除到被除数的个位，没有必要再往下除了（如右图）。

师：你们把63箱和多一些葡萄看成64箱，这里又运用了什么方法？（板书：进一法）

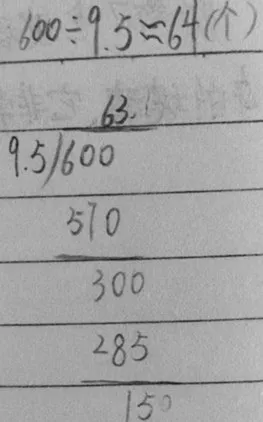
生：葡萄的箱数必须取整数，这个计算结果同样需要取商的近似数。

师：要求宋叔叔能进多少箱葡萄这个问题，你们认为用什么方法取商的近似值比较合理？（板书：去尾法）

师：为什么不能用“四舍五入法和进一法”呢？

生：如果用“四舍五入法”或“进一法”，就是28箱，宋叔叔的钱不够。

师：既然都是取整数箱，为什么所用的方法和第2题又不一样呢？

生：进一法，只要在除得的商的个位上加1就可以了。去尾法，只要取商的值就可以了。

师：下面我们再一起看一下解决这三个问题的方法和计算结果，对比一下，有相同的地方吗？有不同的地方吗？

生：都符合除法的意义，要用除法解决问题。生：计算结果都适合用近似数表示。生：商取近似数的方法各不相同。师：同样是取商的近似值，为什么选择的方法却不同呢？

生：要根据实际情况选择合理的方法。在需要取近似数的情况下，一般用“四舍五入法”取商的近似值，但有时却不适合用“四舍五入法”求近似值。

在解决实际问题的过程中，引导学生根据实际情况合理选择方法求出商的近似值，加深对四舍五入法、进一法、去尾法等取近似值方法的体验。学生在联系所求问题计算6.3÷0.8、600÷9.5、1320÷48的过程中综合运用小数除法单元的相关知识，进一步明确以下两个问题：①计算结果需不需要取商的近似数？②如果需要，用什么方法取商的近似数比较合理？把解决问题的过程和取商近似数的三种方法作为研究对象，通过思辨交流，促使学生的认识深化，不但加深了对“在解决问题时是否要取商的近似数？”“怎样取近似数比较合理？”等问题的理解，而且有助于相互学习借鉴，达成共识。

三、练有梯度，在类比中提升思维

用简单的学习材料做富有思考的训练。在设计本节课的练习时，我们以开放性的数学信息为载体，注重练习内容的前后联系和影响，通过图片信息、多余条件、图文结合等多种形式，优化取商近似值的方法与策略，提升学生的思维。第一层次：引导学生观察图片信息，类比分析“至少需要准备几个这样的小杯？”和“最多能装满几个这样的小杯？”这两个易混淆的问题，巩固“进一法”和“去尾法”的合理选择，进一步明确“四舍五入法”的适用范围。第二层次：结合书本习题，在独立解决问题的过程中，使学生认识到从一步计算解决问题到两、三步计算解决问题“取商近似数的方法”同样适用。同时，引导学生从已有的知识和经验出发，自觉地使用估算，在解决问题的过程中自然地感受到估算的价值。第三层次：拓展取商近似数方法的应用范围，加强算法的比较，以数形结合思想纠正“大面积÷小面积”这种算法，感受策略的优化。

【教学片段】

1.观察与思考

师：下图的信息能看明白吗？谁来告诉我们？

生：一瓶可乐1.25升，倒满一小杯是0.2升。

师：由这些信息，你想到了哪个数学问题？你能把信息和问题完整地说一说吗？

生：一瓶可乐有1.25升，倒满一杯是0.2升。至少需要准备几个这样的小杯？

生：一瓶可乐1.25升，一杯是0.2升。这瓶可乐最多能装满几个这样的小杯？

师：这两个问题会解答吗？说说你的想法。

生：都是求1.25里有几个0.2，1.25÷0.2。

师：算式一样，那这两个问题的计算结果也应该一样？

生：不一样。至少需要准备几个这样的小杯？适合用“进一法”取商。而最多能装满几个这样的小杯，则用“去尾法”取商比较合理。

师：通过比较，我们知道了在计算结果需要取近似数的情况下，要合理选择取商近似值的方法。

2.解决书本习题

教师出示题目，如下：

师：谁愿意来交流一下，你是怎么解答的？

生：先求出剩下的钱，剩下的钱÷笔的单价＝笔的支数，（80-45.6）÷2.5≈13（支）。

生：去尾法合理，即使有剩余的钱也买不到1支笔了。

师：根据这些信息，你还能提出其他问题吗？生：一本相册多少元？45.6÷8=5.7（元）。

生：这些钱全部买相册，最多可以买几本？

师：这个问题的计算结果需要用近似数表示吗？

生:我认为需要，80÷5.7≈14（本），用“去尾法”取商的近似数比较合理。

教师出示另外一道题目：葡萄园李经理为了保护自己的品牌，请设计师帮助设计了一种正方形防伪标志（如右图）。请问：在一张长14厘米、宽7厘米的长方形纸上，最多可以剪出这样的防伪标志几个？

（1）独立思考计算。（学生板演不同的算法）

①14×7=98（平方厘米） 3×3=9（平方厘米）

98÷9≈10（个）

②14÷3≈4（个）7÷3≈2（排）4×2=8（个）

（2）交流讲评。

生：先求长方形的面积，再除以小正方形的面积，计算结果适合用“去尾法”取近似数。

生：我不同意用“大面积除以小面积”这种算法。因为这里是“剪”而不是“剪拼”。

生：我也赞同第2种算法，可以画个图。（学生画图说明）

课件演示：

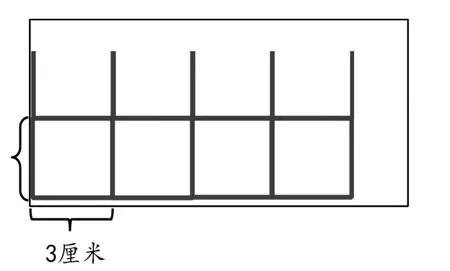
师：数形结合解决问题多好啊！虽然在计算结果时都用到“去尾法”，但解决问题时更要联系生活实际。

结合贴近学生生活的学习素材，设计具有真实性和开放性的问题情境，拓展取商近似数方法的应用范围，充分把握练习的质与量。并在解决问题过程中，鼓励学生质疑，暴露学生的易错点：解决问题时，计算结果需不需要取商的近似数？用哪一种方法取商的近似值比较合理？在讨论、比较、反思的过程中，把感性认识上升到理性认识，从中有所借鉴，用于解决问题实践，获得成功的体验。

总之，学生自己去发现问题、生成问题的过程就是一个深入思考的过程。练习课的教学不能仅停滞于对习题本身的感悟理解上，应当把练习的过程看作是一种创造性活动。其核心并不是多做几道题，而是要把练的主动权交给学生，以“思”引领学生的“练”，注重学生问题意识和良好思维品质的培养，总结出一般的、对以后的学习有启发或帮助的认识与方法。