生产性服务业与制造业协同集聚提升全要素生产率吗？

伍先福

(广西师范大学经济管理学院，广西 桂林 541004)

一、引言与文献综述

在中国城市经济快速发展过程中，生产性服务业与制造业协同集聚的发展张力与影响力逐渐凸显，理由在于：其一，在过多依赖制造业而导致区域经济发展动力日渐衰减的困境面前，地方政府的思维逻辑开始从“制造业优先发展”向“多产业协同发展”转变；其二，面对日趋激烈的市场竞争，以“分离式生产”为特征的传统市场分工所带来的生产效率提升效果越来越不理想，而基于纵向或横向关联的行业或企业因近距离“协同式生产”和“融合性生产”所获得的“外部性绩效”越来越显著，这从根本上驱动着两大产业由“分离式集聚”向“协同式集聚”转型。与此同时，全要素生产率(TFP)增长对中国城市经济发展的内驱力将越来越大。那么，生产性服务业与制造业协同集聚是否促进了中国城市TFP的提升？

既有文献主要从专业化集聚与多样化集聚视角展开探讨。从专业化集聚看，Melo et al.(2009)对集聚经济与生产率间关系的重要文献进行了梳理，发现34项研究中有31项成果表明了集聚与生产率之间呈现正向关系[1]。而Henderson et al.(1992)从两种集聚类型的对比出发，发现专业化集聚可使企业从同一行业中获益，而多样化集聚则可使企业从整个城市范围内获益[2]。深入研究发现，多样化集聚存在“相关多样化”与“无关多样化”之分[3]，并非所有的多样化都能显著地促进地区经济增长。Boschma和Iammarino(2009)的研究发现，相关多样化对地区经济增长有促进作用，但无关多样化无显著影响[4]。可见，不管是专业化集聚还是多样化集聚、尤其是多样化集聚中的相关多样化集聚，均能从整体上推动区域经济增长和生产率提升。据此，是否可以推导生产性服务业与制造业协同集聚亦能促进生产率的提升？

事实上，产业协同集聚将对生产率提升产生正反两方面的影响。其中，积极作用主要来源于外部性经济和产业间良性互动。一方面，产业协同集聚对生产率提升表现出明显的外部性特征。从MAR外部性看，协同集聚的两产业将共享基于投入产出关联的供需大市场，以及一般集聚经济均能共享的劳动力市场[5]，也可进一步推动知识和技术在企业间的溢出，并使各自企业提升对应的“销售市场”和“要素市场”的学习能力[6]，继而促进生产性服务业与制造业企业生产效率的共同提升。从Jacobs外部性看，不同产业间的知识溢出与学习效应往往更显著，突破性创新常常发生在不同产业的交叉融合过程中[7]，而生产性服务业与制造业协同集聚为两大产业的融合发展提供了良好的契机，不同产业企业间的相互学习效应能带动生产性服务业与制造业自身生产率的提升，进而能推动整个城市经济的增长。从Porter外部性看，技术创新和知识外溢源自企业之间的相互竞争而非垄断[8]，而生产性服务业与制造业协同集聚为企业竞争营造了相对有利的成长环境，且激烈的竞争会使低效率的企业无法在大市场中生存[9]，进而促进协同集聚区的生产率提升。另一方面，构成产业之间及内部的良性互动有利于生产率提升。研究表明产业间毫无关联的多样化集聚并不能推动城市经济增长[4]。生产性服务业在集聚过程中不仅提高了自身的技术扩散率，而且会引导其所服务的制造业企业采取新技术和新工艺，从而整体提升了产业集聚区适应外部市场竞争环境变化的能力[10]。同时，为维系生产性服务业企业与制造业企业间的长期合作关系，下游企业会向其上游企业提供资金进行研发，帮助上游企业进行管理培训、组织生产流程、控制质量以及购买原材料等[11]，这些都将有利于生产性服务业企业生产率的提升。

除上述积极因素外，产业协同集聚对生产率的影响也表现一定消极作用。第一，拥塞效应。产业协同集聚的过程虽然为生产性服务业和制造业企业的投入产出沟通节约了各种交易成本、人才搜寻成本等，但当一个地区的产业集聚过度时，当地的地租、交通、时间等成本就会相应增加，从而不利于企业生产率的提升。Henderson(1986)的研究表明，产业集聚的集聚效应会向拥塞效应转变[12]。第二，沉没成本。由于沉没成本，产业协同集聚区的生产性服务业企业、尤其是制造业企业无法轻易退出某个地区，致使生产率相对较低的企业长久停留在产业集聚区甚至演变成“僵尸企业”，从而会降低相关企业的生产或服务效率。第三，集聚组合。不同性质的集聚组合所产生的外部性经济也通常存在较大差异，越是资本和技术密集的企业，其产生的知识技术溢出效应越强，且其吸收其他企业溢出知识的能力也越强，其对生产率的提升效果相对越理想；反之，则越不理想。

综上，基于具体作用路径，产业协同集聚既可能正向促进全要素生产率提升，也可能负向抑制全要素生产率增长。究竟最终整体作用结果如何，则需视具体作用条件而论。遗憾的是，既有文献尚缺乏这方面的专门探讨。对此，本文拟从实证研究的视角，以中国246个地级及以上城市为观测样本，根据构成产业区位熵的高低形成不同作用条件，并借助经典的面板数据模型加以实证检验。相对于既有研究，本文的特色在于采取层层抽丝逐渐深入的思路，借助虚拟变量来对不同作用条件下的产业协同集聚进行内生分组，并对分组后的IV-GMM实证检验结果进行逐一阐释。

二、模型构建与变量选取

(一)模型构建

借助经典的面板计量模型，可对不同作用条件下产业协同集聚影响全要素生产率的整体结果进行实证检验。在具体模型构建时，由于面板模型存在个体效应与时间效应、固定效应与随机效应之分，如果仅凭主观判断而选取其中的某种模型，则可能因模型选择不当而造成回归结果偏误。对此，比较合理的做法是建立一般性面板数据模型，再通过相关检验将其简化为个体固定效应、双向固定效应、一般随机效应、双向随机效应模型等。由于本文主要研究产业协同集聚与全要素生产率(TFP)之间的因果关系，同时考虑到产业协同集聚与其构成产业区位熵指数之间所存在的内生相互关系，有必要基于构成产业区位熵构建虚拟变量。因此，综合上述理论思路和实践检验需求，本文拟构建如下的待检验模型：

lnTFPit=C+β1lnrit+δD+ηDlnrit+γlnControlt+λt+vi+uit

(1)

其中，TFP(全要素生产率)为本文的被解释变量；r为本文的核心解释变量，代表生产性服务业与制造业协同集聚指数；D表示虚拟变量，Dlnr表示虚拟变量与产业协同集聚指数对数的交乘项；Control为系列控制变量，主要包括经济发展水平、人力资本、禀赋结构、产业结构、城镇化指数、市场化程度、市场竞争度、外资依赖度、政府干预度和基础设施水平等；λt是第t期的截距项，代表第t期对被解释变量的特有效应，也称为“时间固定效应”；vi是选择固定效应模型时各个城市不随时间变化而变化的量，如为随机效应，则没有vi；μ是服从i.i.d.的扰动项，β1、δ、η、γ待估参数。下标i和t(t=2003，…，2014)分别代表第i个城市和第t年。

(二)变量选取与数据说明

1.变量选取

(1)被解释变量。全要素生产率(TFP)采用DEA Malmquist全局超效率指数进行测度，并采用该指数的累乘积形式。测度TFP所需的资本存量K采用永续存盘法进行计算，城市基年基本存量、城市固定资本形成额的测度参照王艺明等(2016)方法，即通过市省固定资产投资比进行折算[13]；投资价格指数遵循单豪杰(2008)思路，即2004年及以前采用分省的固定资产形成价格指数，2004年以后采用分省的固定资产投资价格指数[14]；折旧率设置为10.96%。此外，为尽量减少基年资本存量核算误差引起的资本存量测算偏误，本文选择远离样本考察期(2002～2014年)的1985年作为城市资本存量核算的基年。

(2)主要解释变量。产业协同集聚指数(r)，参照陈国亮和陈建军(2012)、杨仁发(2013)的方法[15][16]，采用产业协同集聚相对指数法进行测度，具体为：

第一步，构建城市i产业j的区位熵指数(LQij)，其计算公式为：

LQij=(eij/Ej)/(ei/E)

(2)

其中，eij表示城市i产业j的从业人员数，Ej表示全国产业j的从业人员总数，ei表示城市i所有产业的从业人员数，E表示全国所有产业的从业人员总数。数据测度上，从业人员一律采用分行业“年末单位从业人员数”来进行衡量。

第二步，构建产业协同集聚指数(ri)，其计算公式为：

ri=1-|LQim-LQis|/(LQim+LQis)

(3)

其中，m为制造业，包括《国民经济行业分类(GB/T4754-2011)》中13～43代码行业；s为生产性服务业，包括交通运输、仓储和邮政服务业，租赁和商务服务业，金融服务业，信息传输、计算机服务和软件业，科学研究、技术服务和地质勘查业等五大产业。

虚拟变量及其交乘项。为具体检验不同作用条件下产业协同集聚对全要素生产率的影响，有必要对产业协同集聚进行内生分组，而比较合理的划分依据便是其构成产业区位熵。具体地，首先将构成产业区位熵指数从小到大(或从大到小)进行排序，然后将其均匀地分为三个等份，再根据大、中、小的分组来生成虚拟变量，并与r产生交乘项。

(3)控制变量。结合TFP影响因素的既有文献，本文主要考虑如下的控制变量。第一，经济发展水平(pgdp)，采用人均地区生产总值来衡量。第二，人力资本(human)，借鉴孙慧和朱俏俏(2016)的方法，采用“每万人高校在校大学生数量”作为代理变量。第三，结构因素，禀赋结构(klo)采用实际资本存量与劳动力就业量的比值来衡量；产业结构(indser)采用各城市市辖区内二、三产业增加值之比进行测度。第四，城镇化指数(urb)，采用通过人口城镇化、经济城镇化、空间城镇化和社会城镇化等4个一级指标及8个二级指标构建的城镇化指数来衡量[17]。第五，市场作用力，首先是市场化程度(mark)，借鉴肖攀等(2013)的方法，采用城镇私营和个体从业人员占城市劳动力就业总数的比重来衡量；其次是市场竞争度(com)，参考孙晓华和郭玉娇(2013)等，采用城市i市辖区内的工业企业数与工业生产总值之比除以城市i市辖区样本年度里企业总数与工业生产总值之比的平均值来近似描述。第六，外资依赖度(FDI)，主要用于检验“效率提升说”与“污染天堂说”，考虑到该指标市辖区数据不全，以各城市全市当年实际使用外资金额占全市GDP的比重来衡量。第七，政府干预度(gov)，使用市辖区一般财政预算内支出占GDP的比重来衡量。第八，基础设施水平(inf)，考虑到数据可得性，采用市辖区人均城市道路面积作为代理变量。

2.数据来源与处理

(1)数据来源与样本遴选。本文选取数据较完整的中国246个地级市作为实证观测对象，并考虑到产业协同集聚活动主要发生在市辖区而采用了市辖区数据，数据主要来源于《中国城市统计年鉴》和《中国统计年鉴》。在时期跨度选择上，由于我国2003年在产业统计口径有着较大调整，本文选取2004～2015年作为取值区间，即2003～2014年的观测数据[注]计算TFP指数的时间跨度为2002～2014年。其中，2002～2003年度的TFP数据对应产业协同集聚及其他变量2003年的数据。其他的均可依此类推。。

(2)数据处理。在具体变量核算或数据整理时，采取如下的处理方法。第一，在测算TFP指数时，劳动力投入数据由“年末单位从业人员数”和“城镇私营和个体从业人员”两个统计变量组成；产出变量数据选取“地区生产总值”来加以衡量，并以1978年为基期的相应省份GDP平减指数对其进行平减处理。第二，考虑到数据的连贯性，将个别变量的个别缺失数据采用插值法进行补充。第三，考虑到各变量因带有一定时间趋势而可能引发异方差问题，并进而可能造成回归偏误，我们对所有变量一律进行对数化处理。

三、实证研究结果及分析

(一)内生性问题及其解决

根据Durbin-Wu-Hausman检验结果，我们发现各模型存在内生性，可能引起回归结果偏误。进一步对主要解释变量和控制变量依次进行Wald内生性检验，发现产业协同集聚指数(lnr)和人均地区生产总值(lnpgdp)为内生变量，即与扰动项存在相关关系，可能是与被解释变量TFP之间存在逆向因果关系所致，这与我们的理论判断相符。一方面，产业协同集聚影响TFP增长，但TFP增长也会反过来影响产业协同集聚发展，一个城市的TFP增速越高，就越能激发当地企业技术研发、产品创新、业务赶超等的动能，也因此能驱动企业利润率的提升，进而推动产业协同集聚的发展。另一方面，虽然人均GDP增长能为TFP提升奠定经济基础，但根据索罗残差公式，TFP本身即是GDP增幅中的一部分，因此一个城市的TFP增长率越高，其人均GDP也一般会相应得到提升。对此，本文以lnr和lnpgdp的滞后一阶、两阶分别作为相应内生变量的工具变量，并用IV-GMM对每个待检验方程进行面板数据回归。

(二)产业协同集聚影响TFP的IV-GMM估计

1.无内生分组的面板回归。如果不进行内生分组，即删除式(1)的虚拟变量及其交乘项，则发现产业协同集聚指数(lnr)的系数显著为负，其系数大小为-0.025(回归结果略)。说明在全国均值水平下，生产性服务业与制造业协同集聚显著抑制了全要素生产率增长，这与既有多数文献认为产业专业化集聚有利于生产率提升的结论存在较大出入，也似乎与我们的现象认知和逻辑推理不符。本文认为其主要原因在于，诚如文献综述所言，产业协同集聚作用于TFP时有着诸多作用力相冲的影响路径，如果负向作用力大于正向作用力，则整体结果为负。而产业协同集聚影响TFP的负向作用力之所以大于正向作用力，一方面是产业协同集聚的整体质量偏低使然，另一方面是某些情形下产业协同集聚与构成产业区位熵指数成反比所致。当其中一个构成产业专业化集聚度低时，根据式(3)，另一构成专业化集聚度越低，产业协同集聚指数相反越高，这种缺乏产业积累沉淀的协同集聚指数自然不利于生产率增长。这是因为此时的产业协同集聚不仅整体规模有限，而且同处一地的生产性服务业与制造业之间的投入产出关联较弱，则外部性经济与产业间良性互动所释放的积极作用力非常有限，使得沉没成本、不良集聚组合等释放的消极作用力相对性大幅攀升，从而造成整体结果为负的局面。可见，产业协同集聚影响TFP增长的作用规律不能一概而论，而是应基于构成产业区位熵指数内生分组的前提下，对不同组别中的具体作用规律进行分别阐述。

2.内生分组后的IV-GMM估计。以构成产业区位熵指数低为参照组，分别根据生产性服务业区位熵指数与制造业区位熵指数生成虚拟变量gmr2、gmr3、gsr2、gsr3。如此，式(1)实则演化为分段函数模型，其IV-GMM回归如表1所示。其中，IV-2SLS回归后的豪斯曼检验均支持固定效应模型。

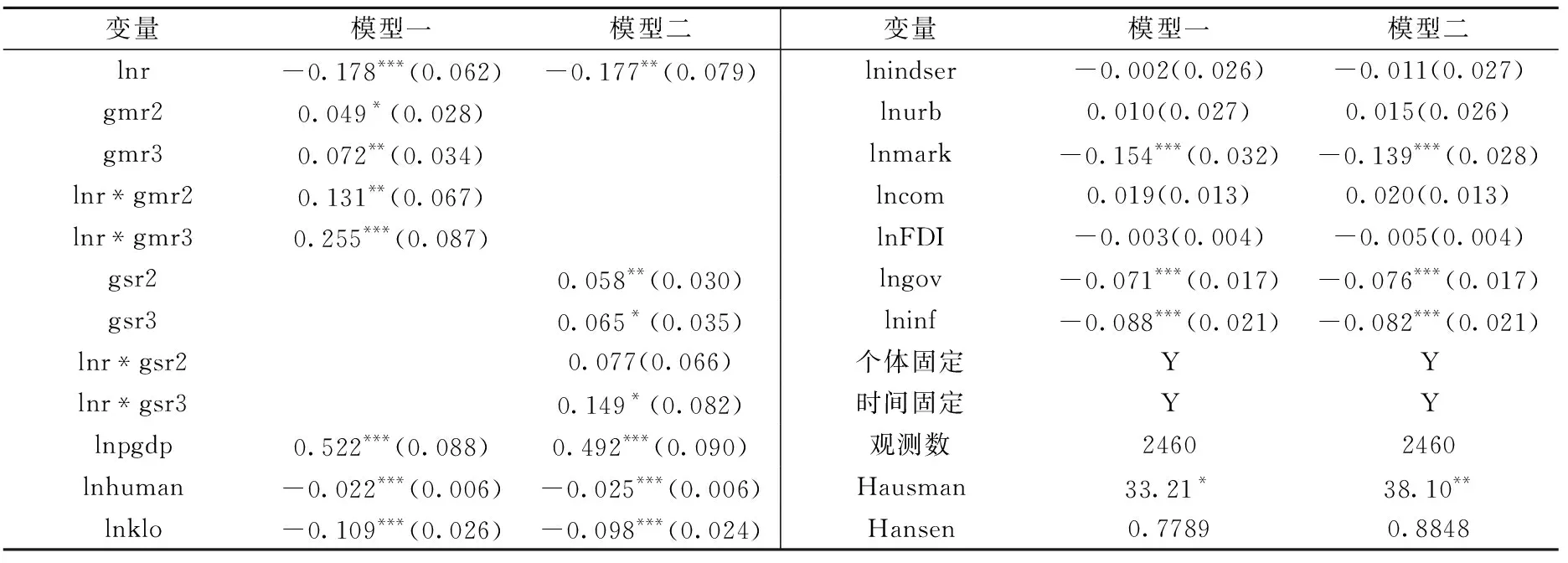
表1 产业协同集聚对TFP影响的IV-GMM面板估计

注：gmr2、gmr3、gsr2和gsr3分别代表制造业区位熵指数中、制造业区位熵指数高、生产性服务业区位熵指数中和生产性服务业区位熵指数高；*、** 和*** 分别表示通过10%、5%和1%的显著性水平检验，括号内为标准误；Hansen检验为P值，其原假设为“所有工具变量都是外生的”；lnpgdp、lnr的工具变量均分别为L(1/2).lnpgdp、L(1/2).lnr。

表1中，lnr的系数显著为负(即参照组)，说明构成产业集聚度低时的产业协同集聚与TFP提升成反比。相对于参照组，构成产业集聚度中或高时的lnr系数已由负转正，且构成产业集聚度高时的系数值大于构成产业集聚中的系数值，说明构成产业集聚度越高，产业协同集聚越倾向于促进TFP增长。为进一步分析构成产业中或高时的产业协同集聚边际影响系数，我们将表1两个模型对应的分组方程撰写出来，其结果如式(4)、式(5)所示。其中，Control代表所有控制变量，A代表所有控制变量的回归系数矩阵。

(4)

(5)

根据式(4)，我们发现在不同制造业区位熵指数作用下，lnr对lnTFP的影响存在质的差异。在制造业区位熵指数高、中、低3个方程中，lnr的边际影响系数分别为0.077、-0.046和-0.178。也就是说，如果制造业区位熵指数高，则生产性服务业与制造业协同集聚能显著地促进TFP增长，否则就会显著抑制TFP增长。而在另两组的抑制力大小上，如果制造业区位熵指数低，则其与生产性服务业协同集聚对TFP的抑制力更大；如果制造业区位熵指数中，则其产业协同集聚对TFP的抑制力明显减弱。可见，随着制造业区位熵指数的提升，生产性服务业与制造业协同集聚对TFP的影响将由负转正，其临界点大约在全国制造业区位熵指数水平值的2/3处。而之所以跨过制造业区位熵指数2/3阈值后的lnr边际系数整体为正，主要是因为：第一，跨过阈值后的制造业集聚已具备相对较大的产业规模，使得此时的制造业集聚与生产性服务业集聚对TFP的正外部性力量能充分释放；第二，跨越阈值后的生产性服务业与制造业之间的良性互动趋于频繁，促成两大产业间的投入产出关联不断得到强化，由此交互作用而成的产业协同集聚较好地满足了Jacobs正外部性的作用条件，因而能更好地发挥出对TFP提升的整体带动力；第三，跨域阈值后的产业协同集聚区，产业之间、尤其是产业内部的企业竞争趋于激烈，迫使协同集聚区内的企业不断进行技术创新和管理变革，如此能不断强化协同集聚区的Porter正外部性力量；第四，相对于正向作用力，跨域阈值后的拥塞效应、沉没成本、交易成本等负向作用力较小，使得此时的产业协同集聚能有效推动TFP提升。

根据式(5)，在不同生产性服务业区位熵指数作用下，lnr对lnTFP的影响仅存在量的不同。即在生产性服务业区位熵指数高、中、低3个方程中，lnr的边际影响系数均为负，说明不管生产性服务业区位熵指数高或低，相应的生产性服务业与制造业协同集聚均对TFP增长起着抑制作用。不同的是，这种抑制力随着生产性服务业区位熵指数的提高而降低。之所以此时的产业协同集聚边际影响系数始终没有突破由负转正的临界点，其原因可能在于：一方面，由于制造业是生产性服务业的需求部门，制造业一般处于相对超前发展的状态，只有制造业区专业化集聚具备较强竞争力，其与生产性服务业协同集聚才能推动TFP增长；另一方面，生产性服务业区位熵指数高、中、低的分组仍过于粗陋，随着产业协同集聚对TFP的边际作用系数不断趋近于零，在分组数足够多的前提下，必然在生产性服务业区位熵指数最高的那组中出现lnr边际作用系数为正的情形。

3.基于构成产业专业化集聚影响的进一步探讨。我们分别以制造业集聚指数、生产性服务业集聚指数替代产业协同集聚指数对式(1)进行回归，发现无内生分组时，制造业集聚倾向于抑制TFP提升(系数为-0.013)，而生产性服务业集聚能显著促进TFP增长(系数为0.037)。内生分组后的回归结果如表2所示，我们发现当制造业集聚指数低或生产性服务业集聚指数低时，制造业集聚对TFP的边际影响显著为负(模型一)或倾向于为负(模型二)，其余情形的边际影响系数基本为正但表现出量的差异，说明制造业集聚度越高越有利于TFP提升，而生产性服务业集聚度越低才越有利于TFP增长。

表2 构成产业专业化集聚对TFP影响的IV-GMM面板估计

注：LQ根据式(2)计算，在模型一、二代表制造业集聚指数，在模型三、四代表生产性服务业集聚指数；gmr2、gmr3、gsr2和gsr3同表1；*、** 和*** 分别表示通过10%、5%和1%的显著性水平检验，括号内为标准误；控制变量及检验结果略。

综合表1、2，我们发现构成产业专业化集聚与产业协同集聚影响TFP时的内在关联。在很大程度上产业协同集聚抑制或促进TFP提升的结果，正是其构成产业专业化集聚对TFP边际作用力的整体合力使然。当制造业集聚程度低时，制造业集聚对TFP的抑制力与生产性服务业集聚对TFP的推动力交相作用(表2的模型一、三)，造成产业协同集聚影响TFP的整体合力显著为负(表1的模型一)。当制造业集聚程度高时，制造业集聚与生产性服务业集聚均能有效推动TFP提升，其相应的产业协同集聚自然有利于TFP增长。当以生产性服务业集聚程度作为分组依据时，制造业集聚均倾向于抑制TFP提升(表2的模型二)，生产性服务业均能促进TFP增长(表2的模型四)，但两者交相作用所形成的产业协同集聚合力仍然为负(表1的模型二)。可见，相对于生产性服务业集聚而言，制造业集聚在产业协同集聚中所能发挥的作用更大。只有当制造业集聚有利于TFP提升时，相应的产业协同集聚才能推动TFP增长。一旦制造业集聚不利于TFP提升，即便此时的生产性服务业有利于TFP提升，相应的产业协同集聚仍然不利于TFP增长。

(三)稳健性检验

除采用单豪杰(2008)资本存量测算的MI指数作为被解释变量进行验证外，本文还采用以张军(2004)资本存量测算的MI指数作为被解释变量对式(1)进行验证(结果略)，发现其IV-GMM回归结果基本一致。同时，本文采用传统的IV-2SLS方法对表1涉及的两个模型进行重新回归(结果略)，发现两个方程不论在系数显著性、系数符号还是系数值大小上，均与表1非常接近，这说明因本文选用数据的异方差问题而引起的偏误不大，也再次证明采用IV-GMM得出的结论是稳健可信的。

四、结论与政策建议

在理论综述的基础上，本文以中国246个地级及以上城市2003～2014年的面板数据为观测样本，通过构建经典面板模型并借助IV-GMM回归进行检验，结果发现中国城市产业协同集聚对全要素生产率的影响呈现非线性特征：随着制造业区位熵指数的提升，生产性服务业与制造业协同集聚对TFP的影响将由负转正，其临界点大约在全国制造业区位熵指数水平值的2/3处；随着生产性服务业区位熵指数的提升，虽然生产性服务业与制造业协同集聚对TFP增长均表现出抑制作用，但其抑制力随着生产性服务业区位熵指数的提高而降低。

基于上述结论，本文提出如下的政策建议。首先，产业协同集聚的“双轮驱动”战略不宜在全国范围内全面铺开，这种战略相对而言更适合于在制造业集聚程度较高的城市推广。在制造业集聚程度相对较低的城市，应重点考虑制造业专业化集聚发展道路，并通过制造业的优先发展来带动生产性服务业的内生性增长。如果不顾城市专业化集聚实际而盲目推进“双轮驱动”战略，则可能不仅会抑制该城市全要素生产率提升，而且会因该战略实施导致的资源错配而破坏整个城市经济的良性循环。其次，应采取有效措施切实提升产业协同集聚区的构成产业专业化集聚质量，注重产业集聚的高质量发展、尤其是技术进步。可以说，越是高质量的专业化集聚，越是容易形成有利于MAR、Jacobs、Porter等正外部性力量释放的氛围和平台，就越能推动专业化集聚及相应产业协同集聚对TFP的增长。最后，基于短期发展目标，可针对所在城市专业化集聚程度来确定其产业协同集聚的差异化发展目标。从制造业专业化集聚视角看，当其专业化集聚度低时，应以产业协同集聚对技术进步的推动效应为主要目标，并警惕产业协同集聚对效率改善和规模变化的消极影响。随着制造业专业化集聚度的逐渐提升，应适时将产业协同集聚的主要目标定位到效率改善上，并警惕技术进步可能停滞不前的消极影响。从生产性服务业专业化集聚视角看，应始终将产业协同集聚对技术进步的推动效应作为主要目标，并警惕此时对效率改善的消极影响。