有限混合费希尔分布极值分布的收敛速度

韦 杰，曾 萍

(贵阳中医学院信息工程学院，贵州贵阳 550025)

20世纪30年代，由Fisher和Tippett提出的三大极值类型分布定理，奠定了经典极值理论的基础[1].趋于极值分布的收敛速度问题一直是极值理论研究中非常重要的课题，当前已经取得了一些成果[2-3].费希尔分布的概率密度函数[4]为

其中m，v表示自由度(m>0，v>0).

定义1设X1,X2,…,Xr是独立随机变量序列，且Xk～Fmk,vk(x)(k=1,2,…,r),Fmk,vk(x)是费希尔分布的分布函数.定义如下随机变量：

(2)

则称T是由r项费希尔分布混合生成的分布，FT(x)为它的累积分布函数.

近年来，关于有限混合分布极值分布类型和收敛速度的研究已经取得了许多有意义的成果，如Cheng等[5]研究了有限混合正态分布、有限混合柯西分布和有限混合指数截尾分布等分布的极值分布类型，Peng等[6]研究了有限混合指数分布极值极限分布的收敛速度.文中研究线性赋范条件下有限混合费希尔分布随机变量序列极值的渐近分布，得到了最大值分布收敛到极值分布的逐点收敛速度.

1 基本引理

下面首先给出费希尔分布尾部表达式及线性赋范条件下最大值的极值分布.

引理1设f(x)和Fm,v(x)分别为费希尔分布的概率密度函数和分布函数，则对充分大的x>0,有

其中，

证明对于x>0，有

根据洛必达法则可得

(6)

结合(5)-(6)式，引理得证. 】

引理2设FT(x)为有限混合费希尔分布的累积分布函数，则对于充分大的x>0，有

证明由引理1知

对于vk>0(k=1,2,…,r),vi0)，有

综上，引理得证. 】

2 主要结论

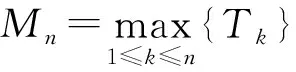
Φv1/2(x)=exp-x-v1/2，

则存在赋范常数

使得

证明由引理2，对于充分大的x>0，有

(8)

进一步

根据引理2和文献[7]推论1.12,FT∈Dl(Φv1/2).所以存在tn使得n(1-FT(tn))=1.结合(8)式，当n→∞时，有

整理得到

令

则

由文献[8]定理1.2.3，结论成立. 】

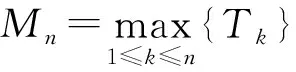
则当n→∞时，下列结论成立:

(1)0

( i )当v1

( ii )当v2=2v1时，有

(iii)当v2>2v1时，有

(2)v1=2.

( i )当2

( ii )当v2=4时，有

(iii)当v2>4时，有

(3)v1>2.

( i )当v1

( ii )当v2=v1+2时，有

(iii)当v2>v1+2时，有

证明令

根据文献[8]定理2.4.2,结论得证. 】