依赖频率的裂缝孔隙介质弹性属性及参数影响

勾彬彬 陈学华* 瞿 雷 吕丙南 蒋 伟 张 杰

(①成都理工大学油气藏地质及开发工程国家重点实验室，四川成都 610059；②成都理工大学地球勘探与信息技术教育部重点实验室，四川成都 610059)

1 引言

裂缝的存在影响储层的渗透率、孔隙度以及流体流动。裂缝介质的岩石物理模型大部分是简化模型，常将裂缝假设为特定的形状(例如扁圆币状)，且分布均匀，定向排列。常见的裂缝模型有：Hudson模型、Schoenberg模型、Thomsen模型、DEM模型、Schelby-Cheng模型等[1]，各种模型有各自的适用范围和条件。Bakulin等[2]分析了Hudson模型和线性滑移模型之间的等价关系； Gurevich[3]结合线性滑移理论和Gassmann方程，直接由背景孔隙岩石弹性参数和干裂缝柔度参数计算等效的裂缝弹性参数，该模型模拟的是低频极限下的情况。

当地震波穿过含饱和流体的地下介质时会引起波致流，导致地震波速度依赖频率发生衰减和频散。在低频极限时，流体对弹性属性的影响可通过Gassmann方程[4]和Brown & Korringa原理[5]的静态模型描述。Gassmann推导了流体对各向同性介质和各向异性介质的弹性模量的影响[4]。由于各向异性Gassmann方程和Brown &Korringa原理涉及大量参数，为了克服这些问题，且得到更直观的结果，Thomsen[6]、Collet等[7]各自重写了基于Brown & Korringa和Gassmann各向异性理论的Thomsen各向异性参数。在更高频率时，弹性波模量比通过Gassmann原理预测的更高。

波致流体流动可依据压力梯度的长度规模划分为三类[8]： 基于波峰波谷压力梯度产生的宏观流、尺度大于孔隙规模但小于波长的介观流、基于裂缝与背景孔隙之间的流体流动形成的微观流，微观流又叫做局部流或者喷射流。依赖频率的弹性模量主要由裂缝的尺度控制[9]，Chapman[10]和Galvin等[11]模拟了该类流体流动。最早的裂缝孔隙间引起的波致流导致的衰减和频散模型由Hudson[12，13]和Chapman[10]做过研究，他们将裂缝模拟为扁圆币状包含在背景孔隙中。Brajanovski等[14]将周期均匀分布于背景孔隙中的高孔隙薄层视为裂缝，结合Schoenberg模型[15]，提出了一种考虑一套平行的平面裂缝嵌入背景孔隙介质的裂缝孔隙介质模型，该模型只能处理裂缝呈周期排列的情况； 随后Kong等[16]基于该模型，考虑裂缝与背景孔隙充填不同流体的情况下的弹性参数计算方法。裂缝孔隙介质常分为硬孔隙和软孔隙，硬孔隙大多是孔隙空间，软孔隙主要影响依赖压力的弹性模量[17-19]。越来越多的研究认为，介观流是地震频段内与流体有关的衰减的重要机制[20]。Collet 等[21]结合压力松弛法[17]和线性滑动变形理论[15，22]，提出了一种新的喷射流模型，它的低(<1kHz)、高(>100kHz)频极限本质上与Mavko等[1]的相同，但最重要的新颖性在于它提供了中频段衰减和速度频散的计算方法，并定义了新的衰减各向异性参数，使该理论能计算含流体裂缝孔隙介质的复数地震速度(该速度是传播角度的函数)，进而能在复数地震速度的基础上计算得到依赖频率的相速度和品质因子。另外，国内学者[23-26]也深入研究了裂缝介质的地震响应特征。

本文主要基于Collet等[21]的喷射流模型，计算了依赖频率的刚度矩阵，基于此，分析了流体替换在裂缝孔隙介质中的影响，主要分析包括背景孔隙度、流体类型、裂缝密度对介质相速度、逆品质因子及各向异性参数的影响。

2 原理与方法

Collet等[21]根据Murphy等[17]和Gurevich等[27]对裂缝孔隙介质模型的研究，设计模型由裂缝形成的软孔隙(半径为r，厚度为h，纵横比α=h/2r)和背景硬孔隙构成(图1)。

图1 Murphy 等[17]的裂缝孔隙介质模型

(1)

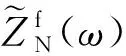
(2)

(3)

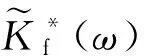
(4)

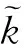
(5)

将式(4)代入式(3)，得到裂缝法向弱度表达式

(6)

(7)

最终其改进模型不考虑背景孔隙流体时依赖频率的刚度矩阵计算公式为

(8)

式中：χb=λb/Lb；ΔT为切向弱度。

最终计算饱和流体依赖频率的弹性模量(刚度矩阵)，据Gassmann各向异性方程[4]，其计算公式为

(9)

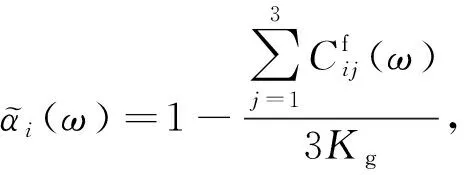
(10)

(11)

只要依赖频率的饱和流体介质的刚度矩阵已知，就可通过Mavko[1]求得依赖频率的介质的纵波和横波速度，该方程为

(12)

式中

M= [(C11-C44)sin2θ-(C33-C44)cos2θ]2+

(C13+C44)2sin22θ

(13)

该方程求得的速度为复速度。相移速度和品质参数可通过复速度求得

(14)

(15)

3 数值模拟与分析

为了分析流体替换在裂缝孔隙介质中的影响，设计砂岩模型，其矿物颗粒体积模量Kg=37.50GPa，干骨架体积模量Kb=21.76GPa，干骨架剪切模量μb=15.91GPa，固体颗粒密度ρ=2.66g/cm3，为了在数值分析中对比不同裂缝孔隙度对纵波速度和品质因子的影响，裂缝孔隙度分别取1.57×10-4和1.57×10-6，其他裂缝及充填流体参数如表1所示。

表1 裂缝及流体参数

图2是不同裂缝孔隙度的砂岩模型在不同入射角情况下纵波速度和逆品质因子依赖频率的变化趋势。当裂缝孔隙度为1.57×10-4时，从图2a可看出，每条曲线都有最小、最大值，在低频和高频极限时趋于平稳，当频率>×103Hz后出现了明显的速度频散，垂向纵波速度值在同一频率时大于水平纵波速度和45°入射角时纵波速度，高低频极限速度之差随着入射角的增大而减小。图2b中可看出，在低频(<102Hz)时，其衰减最小，随着频率的增加，其衰减(逆品质因子)逐渐增加直到特征喷流频率(约为104Hz)，然后随着频率的增加其衰减逐渐减小；另外，入射角越大，其衰减越小，90°入射角情况下，其逆品质因子最小，发生频散和衰减的程度最小。对于裂缝孔隙度为1.57×10-6的情况，图2c、图2d中各个入射角度的纵波频散和衰减值的相对大小与图2a、图2b中反映的特征相似，图2c中的垂直纵波速度最大，但频散程度最弱，45°入射角的纵波和水平速度相对较小，但频散都很显著，且各个入射角的纵波发生频散的频率位置(约在102Hz附近)相对于图2a明显向低频移动，图2c的速度值整体比图2a的大； 图2d的衰减(逆品质因子)量级约为图2b的1/4，其衰减峰值发生在频率约为200Hz处(图2d)，接近地震频带的范围。从图2可见，裂缝孔隙度增加，使各个入射角度的速度降低、衰减(逆品质因子)加剧、发生频散的特征频率向高频移动。

图2 不同入射角情况下依赖频率的纵波速度和逆品质因子(a)、(b)分别是裂缝孔隙度为1.57×10-4时的纵波速度和逆品质因子；(c)、(d)分别是裂缝孔隙度为1.57×10-6时的纵波速度和逆品质因子

3.1 背景孔隙度的影响

为了分析背景孔隙对弹性参数的影响，假定孔隙填充流体为饱和含水流体，分析背景孔隙度的变化对水平纵波、垂直纵波、各向异性参数的影响，其中各向异性参数计算公式[28]为

(16)

图3为孔隙度在0.01～0.20之间变化时，三个入射角度的纵波速度及各向异性参数随频率的变化。在低频段(<103Hz)时，随孔隙度增加，图3a～图3c中各入射角的纵波速度都减小，在高频段(>105Hz)，入射角的纵波速度随孔隙度的变化趋势不明显，且从图3a～图3c可见，随着孔隙度的增加，其介质的衰减频率总体向高频移动。图3d、图3e分别为各向异性参数ε、δ的变化趋势，ε反映纵波各向异性强度的大小参数，δ是连接水平纵波和垂直纵波的过渡性参数，图中没有参数γ，是因为从式(15)中可见，其不受背景孔隙度的影响，随着孔隙度的增加，各向异性参数ε、δ的绝对值变大，说明背景孔隙度的增加使得介质的各向异性参数变强。

3.2 流体类型对纵波速度的影响

地下裂缝或孔隙中通常会充填不一样流体，流体类型的不同会使地质体属性发生变化，了解流体类型对介质属性的影响，对地震综合解释结果至关重要。本文分析了流体类型分别为盐水、油、气三种情况下的不同属性特征，其流体参数见表2。

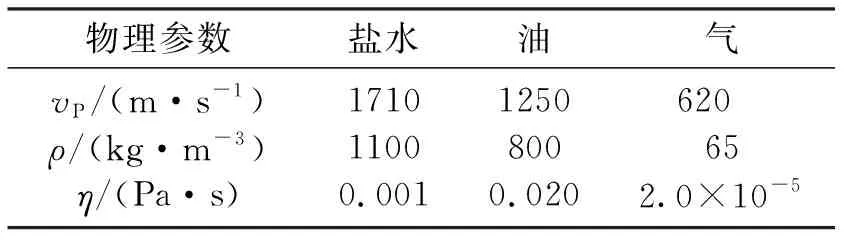
表2 流体的物理参数

从图4可见，在三种不同类型的流体情况下，依赖频率的纵波速度变化差异大，当流体为气体时，高低频速度差异小，相对于其他两种流体情况，含气时的频散程度最小，相当于孔隙或裂缝中无充填流体，只有在极限频率非常高(约108Hz)时出现频散；而当流体为黏滞力最强的油时，速度频散发生的频段在105Hz附近，高低频极限纵波速度差异最大，其差异范围超过1000m/s，发生的频散最显著；当流体类型为盐水时，发生频散的频段在106Hz附近，纵波频散较显著，频散程度处在其他两种流体类型的情况之间，此时高低频极限速度差异数量级为100m/s，也介于其他两种流体类型的情况之间。

图4 含三类流体时纵波速度随频率的变化

3.3 裂缝密度对弹性属性的影响

为了分析裂缝密度e对介质属性的影响，引入Bakulin等[2]的方法，通过比较线性滑动理论模型和Hudson模型，得出裂缝法向和切向弱度计算公式

(17)

(18)

式中：a、c分别为裂缝长、短半轴的长度；k′、μ′分别为裂缝充填物的体积模量和剪切模量；μ为各向同性岩石背景剪切模量；g定义为各向同性岩石背景的横波速度与纵波速度之比的平方。若不考虑裂缝充填物，其法向和切向弱度分别为

(19)

图5a是裂缝密度分别为0.01和0.05时不同入射角度的纵波速度，从中可见当裂缝密度为0.01时(虚线部分)，高低频段的纵波速度差异不大，发生频散的速度范围窄，而当裂缝密度增大到0.05时(实线部分)，各个角度的速度在高低频极限的差异非常明显，发生了显著衰减和频散，说明裂缝密度严重影响介质的频散和衰减。

图5b中虚线、实线分别对应裂缝密度为0.01和0.05时的各向异性参数，可见在同一频率，裂缝密度的增大使各向异性绝对值增大，说明裂缝密度的增加使介质各向异性增强。从全频带范围看，当裂缝密度为0.05时，低频段(<103Hz)和高频段(>105Hz)各向异性参数变化非常明显，说明各向异性参数的大小也随着频率的改变发生了显著的变化。

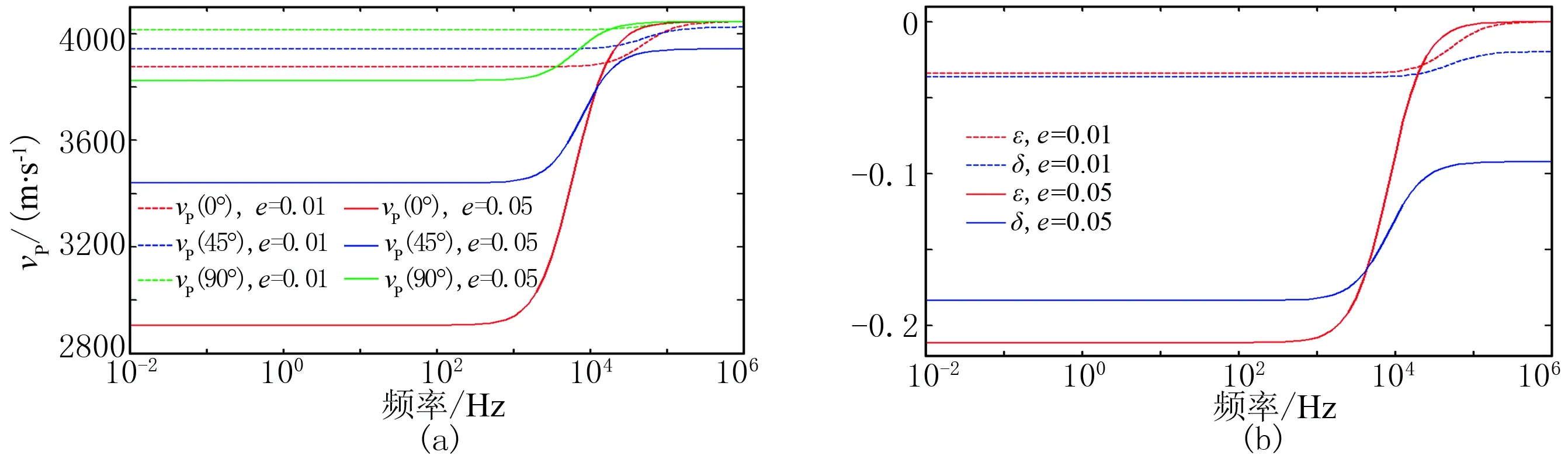
图5 不同裂缝密度下的弹性属性(a)纵波速度； (b)各向异性参数

4 结论

本文通过结合Collet喷射流裂缝介质模型，计算了依赖频率的孔隙裂缝介质弹性刚度系数，计算了等效介质的相速度及逆品质因子，发现入射角的不同也会使介质的相速度、频散和衰减发生改变，显示出不同的趋势变化特征。背景孔隙度的改变也会影响介质的弹性性质，随着孔隙度的增加，在低频段(<103Hz)时，等效介质的相速度减小明显，而在高频段(>105kHz)时，其无明显改变，同时孔隙度的增加也会使介质的各向异性增强。当孔隙中含气时，其发生的频散和衰减相对最小，接近于干孔隙介质，而含油时，介质发生频散和衰减的程度最显著，而含盐水裂缝孔隙介质次之。最后分析了裂缝密度对等效介质的相速度及各向异性参数的影响，发现裂缝密度的增加使介质速度发生频散和衰减程度增大，高低频极限差异大，且增大了介质的各向异性。通过数值模拟的对比分析，裂缝孔隙度的变化使纵波频散的频段发生变化，可接近地震频带，因此，本文的数值分析对于理解地震和微地震中裂缝诱发孔隙介质的速度频散和衰减的机理具有启示作用。

感谢成都理工大学优秀科研创新团队培育计划(KYTD201410)对本项研究工作的支持。