高中数学函数题多元化解题例析

丁 颖

(江苏省常州戚墅堰实验中学 213000)

高中数学中函数的问题包含众多重难点，也是学生学习中反馈问题最多的知识模块.对于面临升学压力的高中生而言，各种训练题、模拟题层出不穷，尽管不提倡题海练习，但多数学生和教师依旧疲于奔命、乐此不疲.从题海中多加锻炼提升学生应试能力，但究竟何处是岸？培养学生一题多解，进行多元化解题，可以从经典例题中寻求解题突破，培养高效解题习惯，发挥经典函数题目的资源优势.结合几例高中数学函数题，阐述多元化解题，突破函数解题思想禁锢.

一、多元解题的思维模式

1.发散思维

数学函数解题中多元化解题方式是以综合角度进行思考，学生们在练习过程中，摆脱传统例题教学中一种解题方案的狭隘认识，通过一题多解的训练方法，为学生建立系统、全面的知识网络，从一个任务目标出发思考多种解题可能性，提供多元化的解题方案，发散思维的应用拓展解题思路.

2.逆向思维

思维过程具有方向性，逆向思维在多元化函数解题过程中同样扮演着重要的作用.一些函数问题从条件入手会变得复杂，尝试从问题倒推可能会有不同的解题办法，运用逆向思维可以摆脱正向思维的禁锢，提供更多解题方案.

3.创新思维

创新思维可以改变单一命题结论、形式，在解题思路上形成多元，从命题角度分析解决问题的可能性，从命题形式、内容、解题能力、思维方式等方面进行创新，使学生的思维更加灵活，激发解题创造力和创新能力.

二、高中数学函数多元解题例题探析

1.关于函数值域问题的多元化例题解析

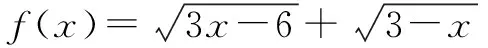
分析确定该题是无理函数的求值域或最值的问题，在高中数学函数解题中经常遇到，在各种模考卷和高考题中算常见类型.题目短小精悍，但解题方法多样，可以涵盖高中阶段众多数学知识，对学生知识的综合应用能力和解题思路的锻炼十分有益，体现学生的数学核心素养.

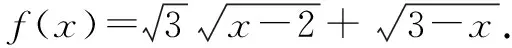
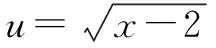
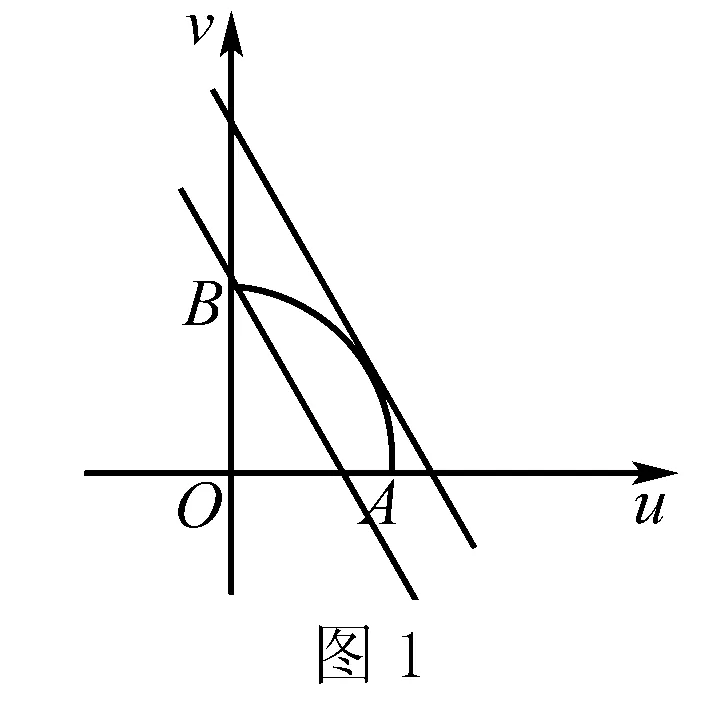
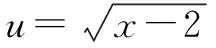
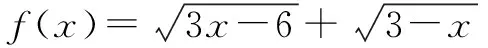
此外，该题目还可以借助一阶导数以及函数的单调性求解，或者借助二阶导数和函数的凹凸性求解.由于文章篇幅有限，不再一一赘述，提供上述常用且学生容易掌握的几种解题思路，以便参考.

三、函数最值问题的多元化解题探析

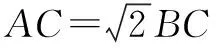
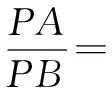
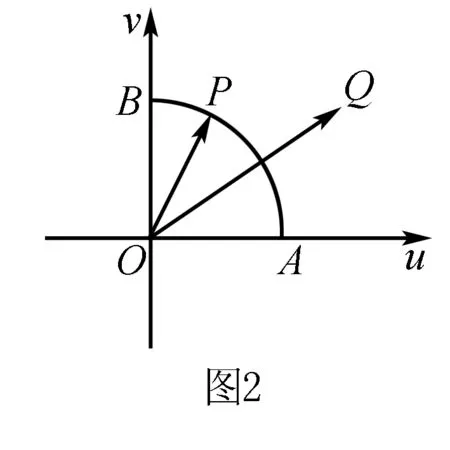
方法1 借助三角函数和函数相关知识解题.

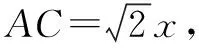
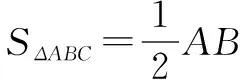
根据余弦定理可得

代入①式，

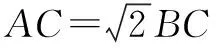
从该例题的解题方法可见，方法2具有原理一致性,在“阿波罗尼斯圆”的理论背景下解决的,所以我们主要是理解“阿波罗尼斯圆”的由来及其概念,而并非一定需要使用其相关结论来解决问题.