基于有限元法的试验台电动机支座模态分析与结构改进

黄小天，李 明，孙炜海，祝国荣

(1.陆军装甲兵学院 车辆工程系，北京 100072；2.北京北方车辆集团有限公司，北京 100072)

电动机是车辆传动装置试验台常用的动力输入设备。电动机支座(下述简称支座)起到支承和固定电动机的作用，同时方便设备安装，可适应不同型号试验台及不同安装环境。对电动机及支座进行模态分析，确定支座的振动参数，通过判断支座在各阶固有频率下的振型变化，可以了解支座在电动机工作状况下的振动形式，有利于对支座等试验台机械零部件进行动态设计与改进[1-4]。

模态是机械结构的特有属性，包含固有频率、阻尼比及模态振型。分析模态方法有有限元法和试验分析法，采用有限元法可快速修改设计结构，并进行再次分析[5-8]。本文采用有限元法建立支座的模型，进行模态分析，并提出改进的结构方案。

1 模态分析基础

模态分析是基于线性振动理论，对激励、结构和响应三者的相互关系进行研究分析，主要采用有限元法对结构进行离散化，然后建立系统的特征值问题数学模型，运用各种近似方法以求解系统的特征值及特征向量，即求解系统的固有频率及对应振型[9]。

一般机械结构可以简化为具有n个自由度的系统，其振动微分方程为：

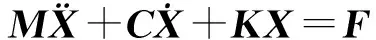
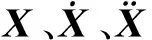
(s2M+sC+K)X(s)=F(s)

令s=jω，则阻抗矩阵表示为：

Z(ω)=(K-ω2M+jωC)

频响函数矩阵表示为：

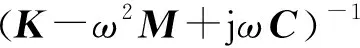
系统运动方程表示为：

(K-ω2M+jωC)X(ω)=F(ω)

再引入模态坐标：

X(ω)=Φq

式中，Φ为振型矩阵；q为模态坐标。则有：

(K-ω2M+jωC)Φq=F(ω)

将其中各矩阵对角化，两边同乘以ΦT，则：

(K-ω2M+jωC)q=ΦTF(ω)

对于每一个固有频率ω，都可以确定一组振型矩阵Φ，为所要求的固有振型。

2 支座模态分析

2.1 改进前支座的模态分析

2.1.1 仿真模型的建立

支座主要由结构钢构成，其高度为670 mm，长度为1 100 mm，宽度为750 mm。在试验台实际使用中，当电动机调速到3 000r/min时，电动机及支座系统振动明显。将支座的几何模型导入到ANSYS软件中，由于电动机几何模型复杂，这里根据电动机的质量及外观尺寸建立电动机的简化模型。由于质量对模态分析结果的影响明显，因此应保证简化的电动机模型质量质心位置与原电动机的质心位置保持一致。采用实体单元划分网格，单元尺寸设置为12 mm。最终划分单元数目为118 499个，节点为342 891个。划分网格后的模型如图1所示。

图1 支座的有限元模型

支座为结构钢焊接而成，根据机械设计手册，取密度为7 850 kg/m3，弹性模量为200 GPa，泊松比为0.3。模态分析为线性分析，不考虑非线性分析中的不同接触类型，结合实际情况将所有接触类型设置为绑定约束。约束条件对模态分析有重要影响，由于支座通过螺栓将四边固定于铸铁平台，这里通过简化，不对螺栓进行建模，而是在对应螺栓的位置在支座四边加以固定约束，简化模型的同时考虑了主要因素。求解器类型由程序自动选择[10]。对于一般机械结构，其固有频率越低，越容易被外界输入激励起来，高阶模态的模态有效质量一般所占比重较少。本文只关注低阶模态，计算支座的前6阶约束模态进行分析。

2.1.2 仿真结果分析

通过有限元计算，得出支座的前6阶固有频率见表1。四边固定约束条件下支座的前6阶振型如图2所示。

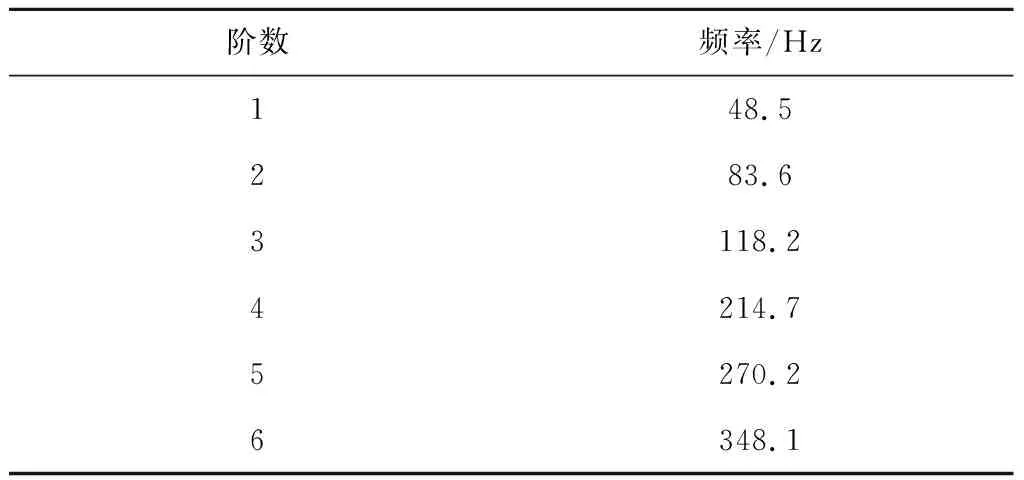
表1 改进前支座前6阶固有频率

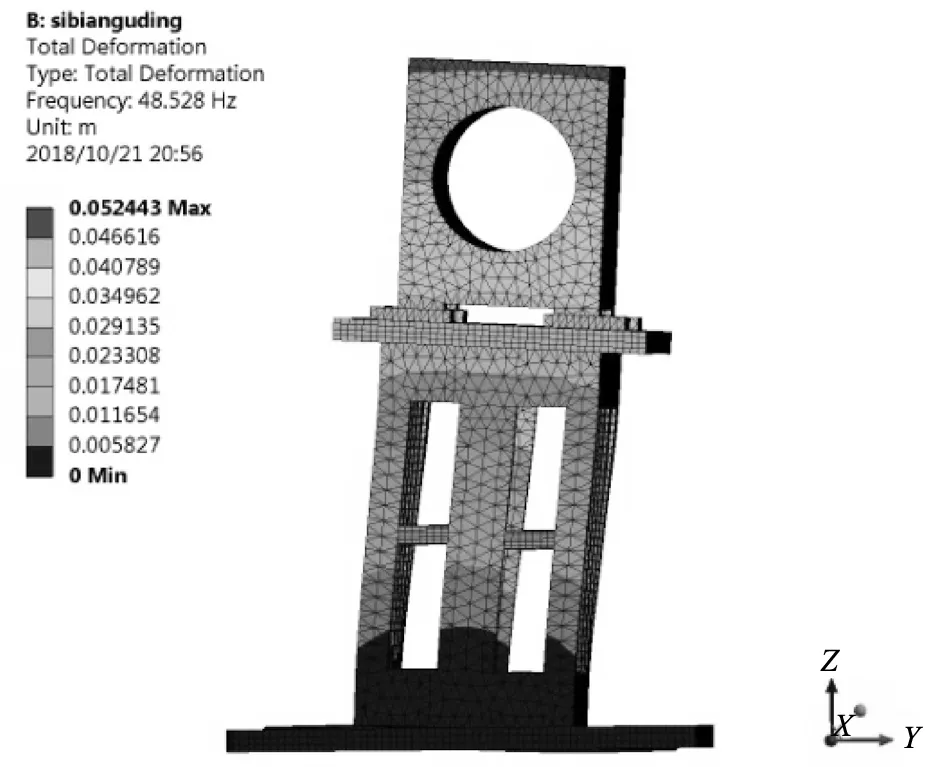
a)1阶振型图

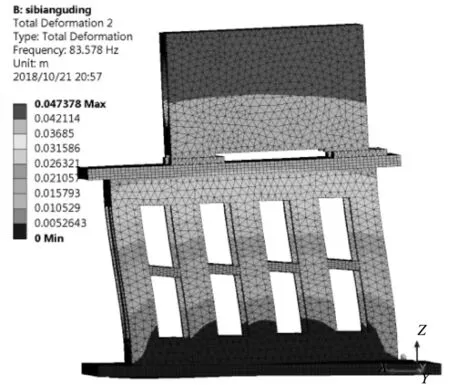
b)2阶振型图

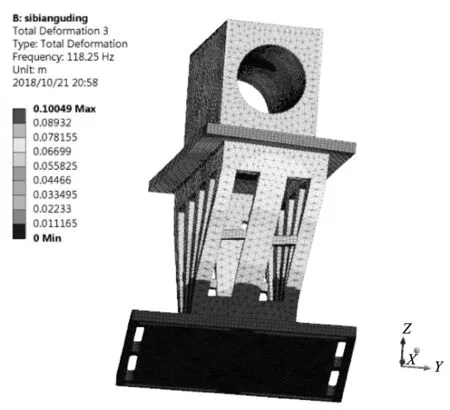
c)3阶振型图

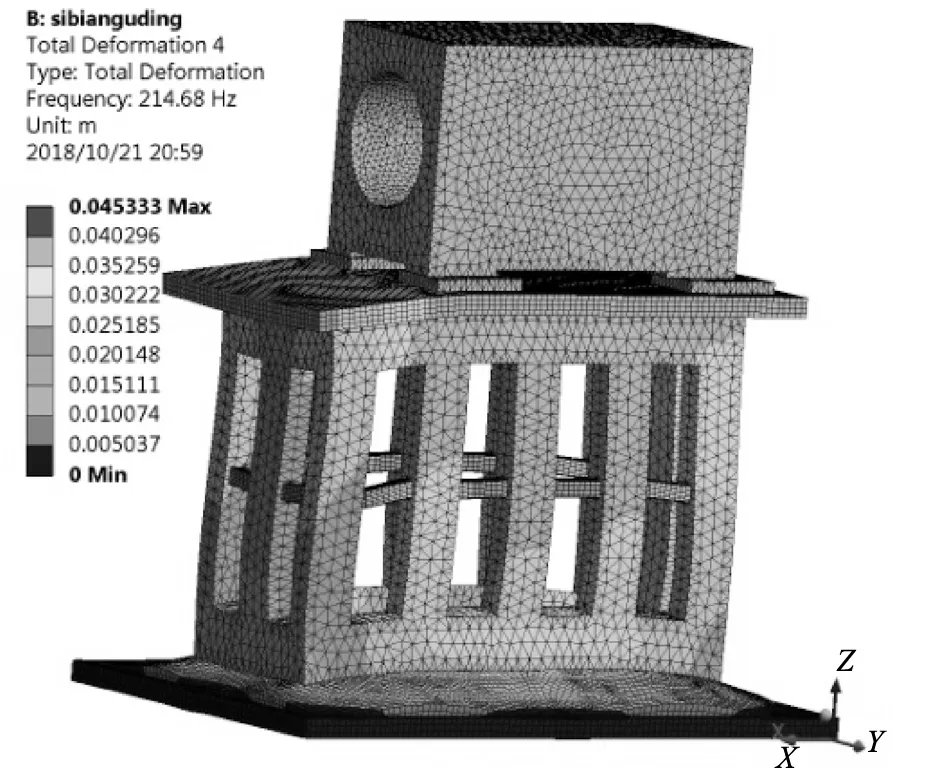
d)4阶振型图

e)5阶振型图

f)6阶振型图

试验台电动机的最大转速为6 000 r/min，换算成旋转激励频率为100 Hz。当电动机达到其最大转速时，即当支座的固有频率<100 Hz时，在电动机高转速时会发生共振。从表1中可知，该支座的1阶和2阶固有频率分别为48.5和83.6 Hz，均<100 Hz，且试验台运行时约3 000 r/min时发生共振，此时电动机的旋转激励频率为50 Hz，非常接近1阶固有频率48.5 Hz，发生共振；因此，应改进支座的结构设计，以避免在电动机的运转范围内支座发生共振。

从图2中可以看出，支座1阶约束模态振型为沿y方向的整体左右摆动，2阶约束模态振型为沿x方向的整体前后摆动，3阶约束模态振型为在xy平面内的扭动，4阶约束模态振型为沿z方向的上下振动，5阶约束模态振型为沿y方向的中间和上下两端反向的振动，6阶约束模态为沿x方向的中间和上下两端反向的振动。支座的1阶和2阶约束模态振型为整体的前后或左右摆动，主要是由于刚度不足导致。

2.2 改进后支座的模态分析

对支座进行结构改进，主要考虑提高支座的低阶固有频率，尤其是1阶和2阶固有频率。由于支座是用来支承电动机的，所受载荷来自于电动机高速旋转时产生的振动。电动机工作时的转速越高，电动机的旋转激励频率越大，因此对支座进行改进主要是考虑提高动刚度。

动刚度是指机械结构产生单元振幅时所需要的激振力，在激振力一定的情况下，结构动刚度越大，其产生的振幅越小，结构的抗振动能力越强。对于多自由度线性系统，其动刚度公式为：

Kd=k-ω2m+iωc

其中，Kd为动刚度矩阵；k为静刚度矩阵；ω为激振频率；m、c分别表示质量矩阵及阻尼矩阵。可见通过提高结构的静刚度矩阵可以提高其动刚度，而提高结构的静刚度可采用加肋板、改变支座的高宽比等方法。

由于电动机的中心高固定，不能改变支座的高度，因此可考虑增加支座宽度或在支座上增加肋板，以此提高支座结构的静刚度。对改进后的支座应用ANSYS软件进行模态分析，步骤与前面类似，划分网格、材料和边界条件设定与前面相同，计算前6阶固有频率和模态振型。

计算得到改进后的四边固定约束支座的前6阶固有频率见表2。对应的改进后的支座前6阶振型图如图3所示。

表2 改进后支座的前6阶固有频率

a)1阶振型图

b)2阶振型图

c)3阶振型图

d)4阶振型图

e)5阶振型图

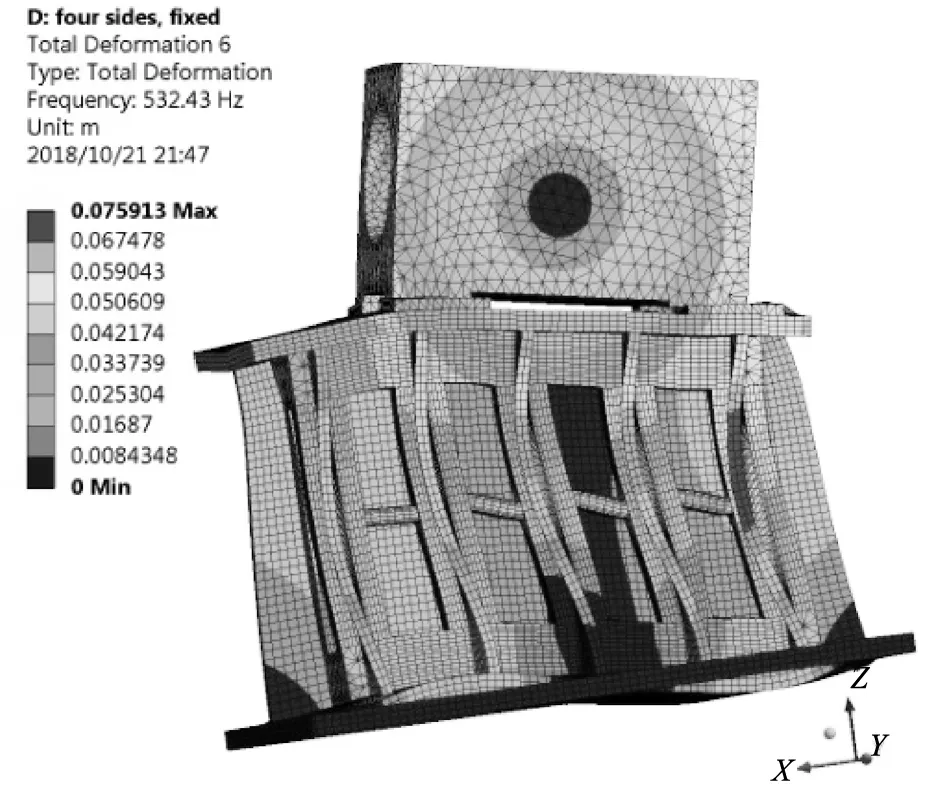
f)6阶振型图

由表2可知，支座的1阶约束模态固有频率为103.4 Hz，该频率位于电动机旋转激励频率(0～100 Hz)范围之外，因此改进后支座的振动特性能满足使用要求，不会产生由于调速电动机的旋转激励导致的共振。由于1阶频率为103.4 Hz，过于接近100 Hz，为防止发生共振，应对加工制造过程和安装条件做出要求。

从图3中可看出，改进后支座的1阶约束模态振型为沿y方向的整体左右摆动，2阶约束模态振型为沿x方向的整体前后摆动，3阶约束模态振型为在xy平面内的扭动，4阶约束模态振型为沿z方向的上下振动，5阶约束模态振型为沿y方向的中间和上下两端反向的振动，6阶约束模态为沿x方向的中间和上下两端反向的振动。改进后支座的约束模态振型与改进前类似，改进后各阶固有模态频率有明显提高。

3 结语

基于有限元法和模态分析理论，对支座进行模态分析，获得前6阶固有频率及每阶对应的振型图，通过计算发现，支座的1阶和2阶约束模态频率分别为48.5和83.6 Hz，位于电动机旋转激励频率(0～100 Hz)范围之内，对支座结构进行了改进，提高最低固有频率到103.4 Hz，避免支座在工作过程中出现共振，可为试验台其他零部件的设计与改进提供参考。