一种新的雷达信号脉内分选方法

袁泽恒，田润澜，袁如月，王晓峰

（1.空军航空大学航空作战勤务学院，吉林 长春130022；2.南京大学电子科学与工程学院，江苏 南京210046）

0 引言

由于现代电子信息战的激烈对抗和雷达技术迅猛发展，新体制雷达不断投入使用并逐渐占据主导地位［1－2］，雷达的工作频率覆盖范围更广，信号参数更加捷变，其信号波形在时域、频域等多个域中同时变化，对目前信号的分选识别造成了严峻的挑战。基于载频（RF）、脉宽（PW）、到达角（DOA）以及脉冲重复周期（PRI）等全脉冲参数的分选方法［3－6］，难以对雷达信号辐射源进行有效的分选。

由于脉内特征参数具有相对稳定性，所以现在已经有不少学者将复杂度特征、熵值、相像系数等脉内特征参数成功地应用到雷达信号分选中［7－9］，但是这些研究只是提取利用单一的脉内参数，作为信号分选的辅助参数，主要还是基于全脉冲参数。在当前雷达体制下，这种方法并不能有效提高信号分选正确率。所以本文研究了新的解决方案，选择多个相对稳定的脉内特征参数作为信号分选的主要参数输入。

相像系数在雷达信号分选领域被广泛运用，有大量的实验依据，高阶累积量在对通信信号调制样式的识别中具有明显的效果［10］。所以本文提取相像系数和高阶累积量作为参与分选的脉内特征参数，利用改进的支持向量机，验证分析基于脉内特征参数联合分选的可行性。

1 特征提取

1.1 相像系数

频谱形状的变化蕴含着脉冲信号的频率、相位和幅值的变化信息，在一定程度上也体现了信号能量的分布情况。相像系数具备有效刻化雷达辐射源信号频谱形状的能力。提取相像系数的过程，就是将雷达信号序列离散化后，选择特征明显的信号序列，通过计算得出。选取矩形信号和三角形信号作为参照信号，因为矩形信号的能量均匀分布，而三角形信号的能量分布集中，所以作为参照信号可以真实地刻化雷达辐射源脉冲信号的能量分布状况。构造的矩形脉冲序列U（k）和三角形脉冲序列T（k）的表达式如下所示：

式中，N为脉冲序列的个数。

提取相像系数的具体步骤如下：

1）对雷达脉冲信号进行FFT变换，将信号序列由时域变换到频域，并在频域对信号能量进行归一化处理，得到处理后的信号序列F（i）。

2）计算矩形脉冲序列U（k）和F（i）的相像系数，计算公式如下：

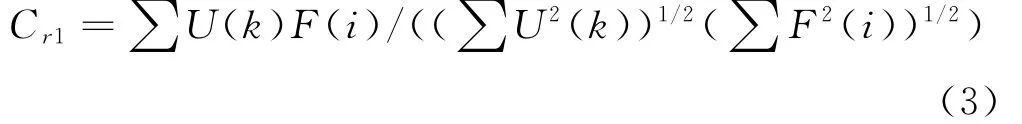
3）计算三角形脉冲序列T（k）和F（i）的相像系数，计算公式如下：

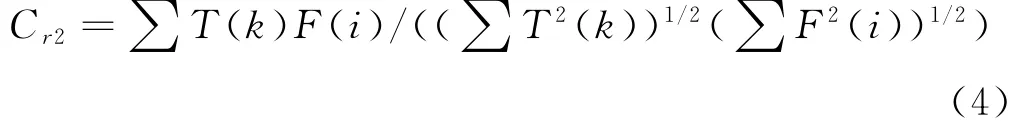
将Cr1和Cr2组成联合的特征向量，即相像系数C（k）＝［Cr1，Cr2］，其中k表示第k个脉冲序列。

1.2 高阶累积量

信号波形的变化蕴含着脉冲信号的频率、相位和幅值的变化信息，在一定程度上也体现了信号能量的分布情况。高阶累积量具备有效区分不同信号波形特征的能力，因此可以作为脉内参数参与分选。

对于长度为N 的复平稳随机信号x（k），其高阶矩可表示如下：

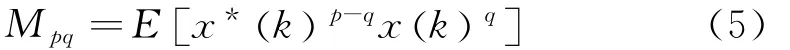
式中，x＊（k）表示复共轭信号。信号x（k）的各阶累积量定义如下：

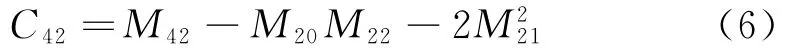
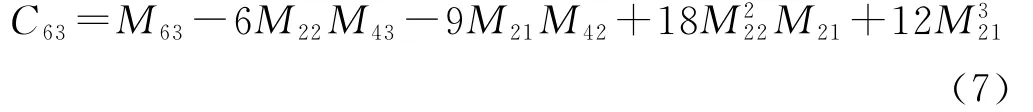
本文采用四阶累积量C42和六阶累积量C63是有依据的，假设中频数字信号的解析形式可表示如下：

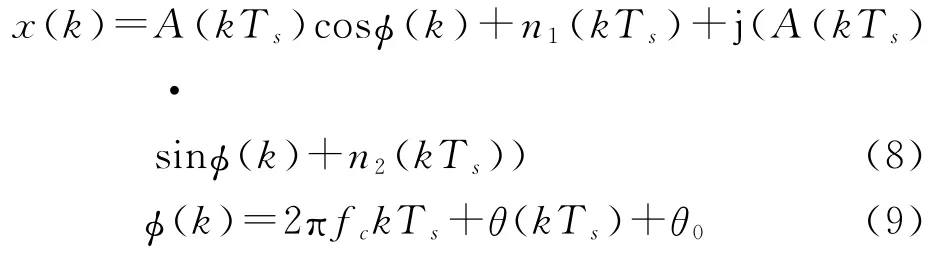
式中，A（kTs）是采样信号的瞬时幅度，（k）为瞬时相位，n1（kTs）和n2（kTs）表示均值为零和方差为σ2的高斯白噪声，fc是载波频率，Ts为采样周期，θ（kTs）表示调制符号的相位信息，θ0表示载波初始相位。四阶和六阶累积量有多种形式，结合式（5）可以发现，当p＝2q时高阶矩完全不受载波频率和载波初始相位的影响，因此选择C42和C63作为高阶累积量的参数值。

1.3 特征值归一化

首先消除高阶累积量的不确定因素，由于侦收到的信号能量未知，导致信号的功率和幅度不确定，所以计算出的高阶累积量的大小也是不确定的。为了解决这个问题，采用估算出的信号功率来对高阶累积量的参数值进行归一化。

实际上接收信号与高斯噪声的总功率，等效其信号的二阶矩M21，所以本文采用式（10）计算信号的功率 P［10］：

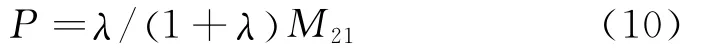
式中，λ为信噪比。

用信号功率对式（6）进行归一化得：

同理用信号功率对式（7）进行归一化得：

将F1和F2组成联合的特征向量，即高阶累积量H（k）＝［F1，F2］，其中k表示第k个脉冲序列。

对于n个脉冲信号，相像系数的特征参数包含Cr1和Cr2两个特征向量，高阶累积量包含F1和F2两个特征向量，共有四维特征参数，此时提取出的样本数据可以用脉内特征参数向量IPCi表示：

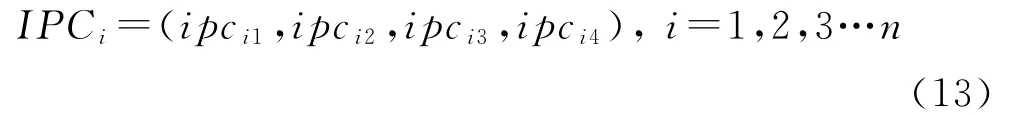
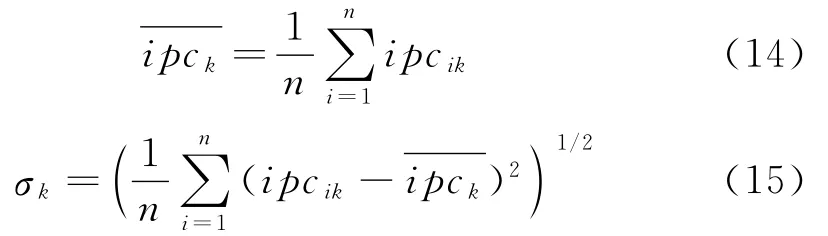
式中，1≤k≤4，由此可得样本脉内特征参数向量的标准化值ipc′ik：

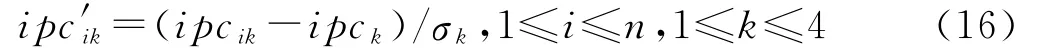
2 脉内多参数分选算法

2.1 支持向量机

由于在利用多参数对雷达信号进行分选时，分类器的性能直接影响着最终的分选结果。目前常用的分类器有神经网络、支持向量机等，神经网络的结构比较复杂，属于一种内部黑箱操作，很难对其参数进行调整，导致产生局部极值等问题。支持向量机（SVM）是根据Vapnik提出的结构风险最小化原则来提高学习机泛化能力的方法。SVM克服了神经网络的不足，能够在小样本、多维度模式下取得全局最优解。

本文采用的SVM是通过利用Gaussian核函数［11］，将数据样本映射到一个高维特征空间中，并在这个高维特征空间中寻找一个能包围所有样本数据映射点的最优超球面，将这个超球面反映射回数据空间，最终得到包含所有数据点的等值线集。

定义相像系数Cr1、Cr2和高阶累积量F1、F2构成四维属性信息的雷达脉内参数描述向量ipc′ik，其数据空间VR4，因为这些脉内特征参数的性质不明确，所以采用高斯核函数把数据映射到高维特征空间，在特征空间中可以寻找一个最小半径为R的闭凸的超球体，对应的约束条件为：

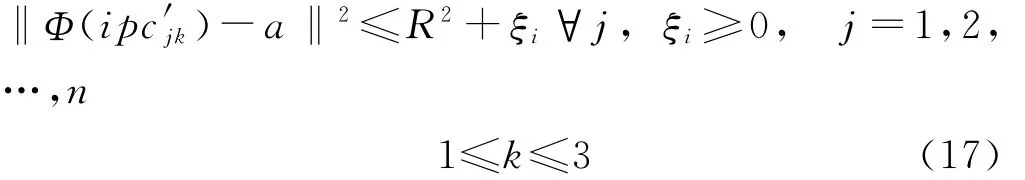
式中，a为超球体的球心；ξi为松弛量；‖·‖为Euclidean范数。式（17）的Lagrangian函数为：

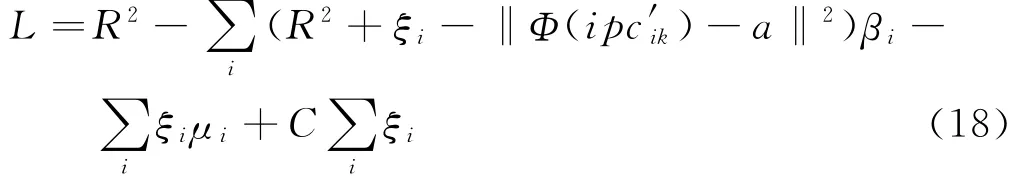
式中，βi和μi均大于零，为Lagrangian乘子；常数C称为惩罚因子。结合KKT条件，得出式（18）的Wolfe对偶形式：

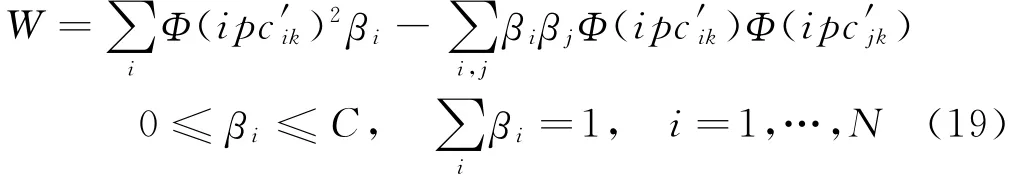
引入Gaussian核函数：

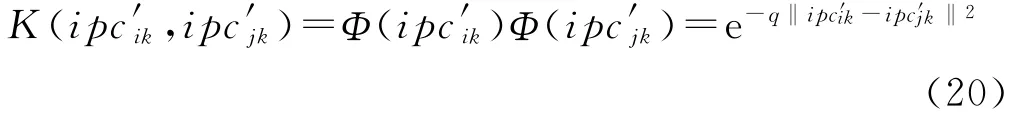
式中，q为Gaussian核的宽度参数，将核函数代入式（19）中得：

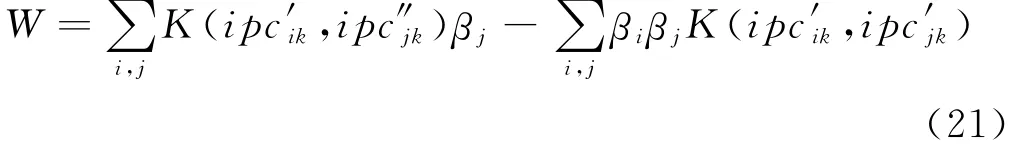
2.2 算法改进

在高脉冲密度的环境下，直接运用上述方法对雷达辐射源信号进行分选，会造成运算时关联矩阵规模庞大的问题，极大地降低其运算速度和分选正确率，而且数据样本之间的不平衡性，一定程度上也会对分选结果产生影响。在支持向量机对信号分选的结果中，其边界受Gaussian核的宽度参数q和Lagrangian函数的惩罚因子C的控制，随着参数q的增加边界表现出更紧的特性，通过参数C的减少可以平滑分类边界。

针对上述问题做出改进，采用基于支持向量机的分层互耦的方法［12］，对数据样本进行分层处理，降低计算时的运算量。其次利用变精度粗糙集对归一化后的脉内特征参数向量计算权重［13］，对数据样本和支持向量机的核函数内积进行加权，稳定数据样本之间的平衡关系，从而避免分选结果被脉内特征参数的弱相关特征影响［14］。同时对分选结果进行分析，构建有效的评价模型，引入稳定的物理量来选择最佳的支持向量机参数q和C，提高分选正确率。具体步骤如下：

1）利用用变精粗糙集对归一化后的样本数据进行处理，得到特征加权矩阵即：

SVM的核函数加权计算公式如下：

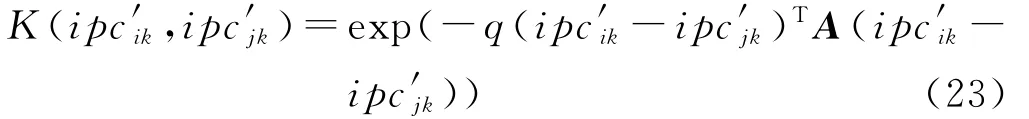
2）从类内耦合度和类间分离度出发，建立分选结果有效评价模型，对分选结果进行分析，引入稳定的物理量G值［15］，从而确定最优SVM的参数q和C。

类内耦合度定义为：

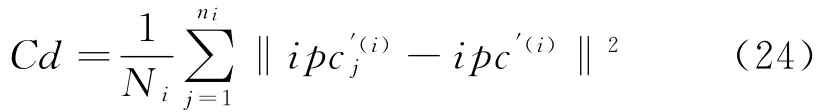
式中，Ni为样本数，i为样本脉冲描述向量的维数。对应的分选后的样本中心为：分离度反映了不同类之间的差异性，定义为：

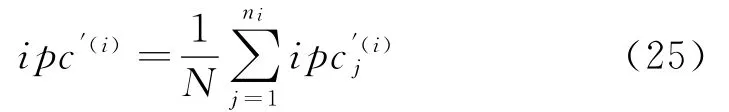
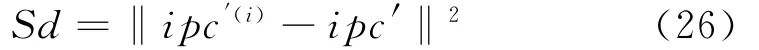
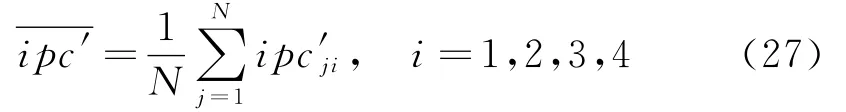
分别将类内耦合度和类间分离度除以相应的权值，然后将两参数进行比较分析，建立对分选结果的有效性评价模型：

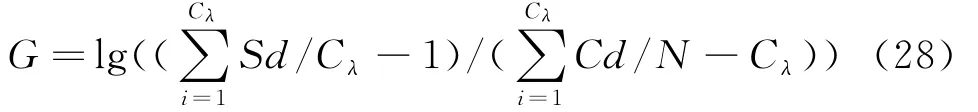
式中，Cλ为对应阈值λ的类数，G值越大，说明类与类之间的差异越大，分选结果也就越好。

2.3 分选流程

如今大量新体制雷达不断投入使用并逐渐占据主导地位，使得基于全脉冲参数进行信号分选的方法失效，所以本文提取相对稳定的脉内特征参数相像系数和高阶累积量，基于改进的分层互耦SVM算法，对雷达信号辐射源有效地进行分选，具体流程如图1所示。

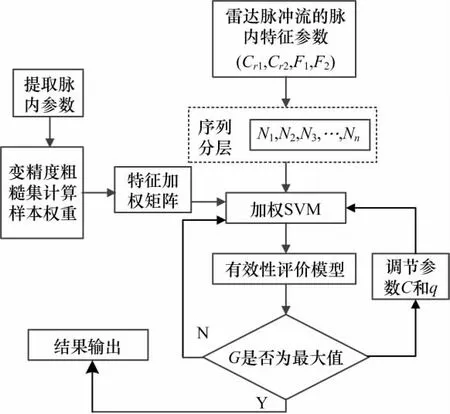
图1 脉内多参数分选流程图

3 算法实验

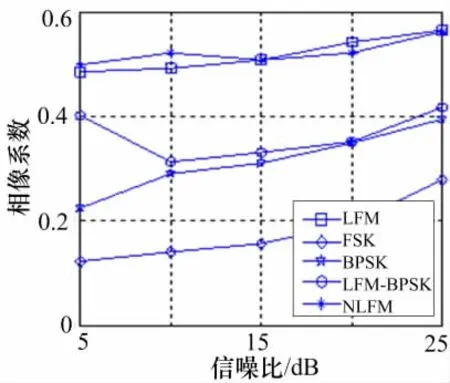
图2 矩形脉冲相像系数

设计雷达数据样本，共5000个脉冲。仿真模拟线性调频信号（LFM）、非线性调频信号（NLFM）、混合调制信号（LFM-BPSK）、频率调制信号（FSK）、相编码信号（BPSK）共五类脉内调制信号，每类调制信号中各有8种雷达类型。首先验证脉内特征参数相像系数和高阶累积量作为参与雷达信号分选参数的效能，然后采用对比的方式证明本文算法的优异性。

3.1 参数验证

验证相像系数Cr1和Cr2，以及高阶累积量F1和F2，分别对不同调制信号分识别能力，以及分析其相互组合的识别效果。仿真结果如图2～5所示。

可以直观地看出，各脉内特征参数具备一定的区分信号样式的能力，但是局限性也很明显。相像系数对频率编码信号（FSK）的区分度很明显，其中在相像系数Cr1的分选识别效果中，LFM和NLFM、BPSK和LFM-BPSK，两两之间存在交叠的现象。虽然在相像系数Cr2中，LFM和NLFM的交叠现象得到弱化，但是BPSK和LFM-BPSK的交叠现象变得更加严重。高阶累积量对LFM-BPSK信号区分能力强，但是对于其它调制信号也存在着不同程度的交叠。其中在高阶累积量F1的识别效果中，LFM和NLFM、FSK和BPSK，难以得到有效的分选。在高阶累积量F2中，LFM和NLFM的交叠状况得到有效改善，FSK和BPSK的交叠状况却趋于恶化。

综上分析，可以得出相像系数Cr1和Cr2两参数联合的识别结果，以及高阶累积量F1和F2两参数联合的识别结果都存在不同程度的差异性和局限性。将相像系数和高阶累积量相结合，可以相互补充消除局限性，对本文设计的五大脉内调制类型信号进行有效的区分。虽然此方法至少将计算复杂度提高了一倍，但是这只是训练分类器的参数准备阶段，可以事先完成，不会增加最终的算法复杂度。

3.2 算法验证

本文利用变精度粗糙集计算雷达数据样本中各脉内参数的权重，构建特征加权矩阵，采用改进的分层互耦SVM算法，从雷达数据样本中随机抽取2000个脉冲进行测试，采用提取雷达数据样本中的相像系数和高阶累积量作为输入参数，评估算法的分选性能。采用文献［14］的方法和Kohonen神经网络方法［16］，进行对比试验。基于上述三种方法进行算法测试实验，仿真结果如表1及图6所示。

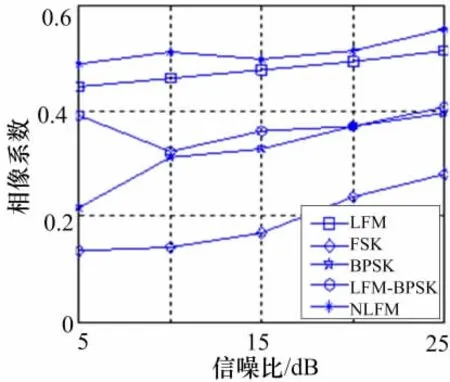
图3 三角脉冲相像系数

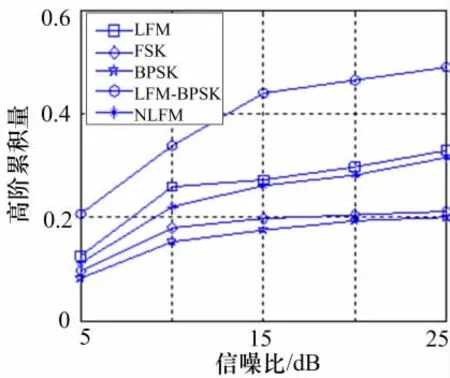
图4 高阶累积量F1

从上述图表中可以明显看出，虽然本文方法与文献［14］方法得出的分选正确率相差无几，但是本文方法的时间复杂度更低，信号处理速度相对较快。在信噪比小于10dB的环境下，本文方法的分选正确率更高，所以相比于其它两种方法，本文方法的低信噪比适应性更好。

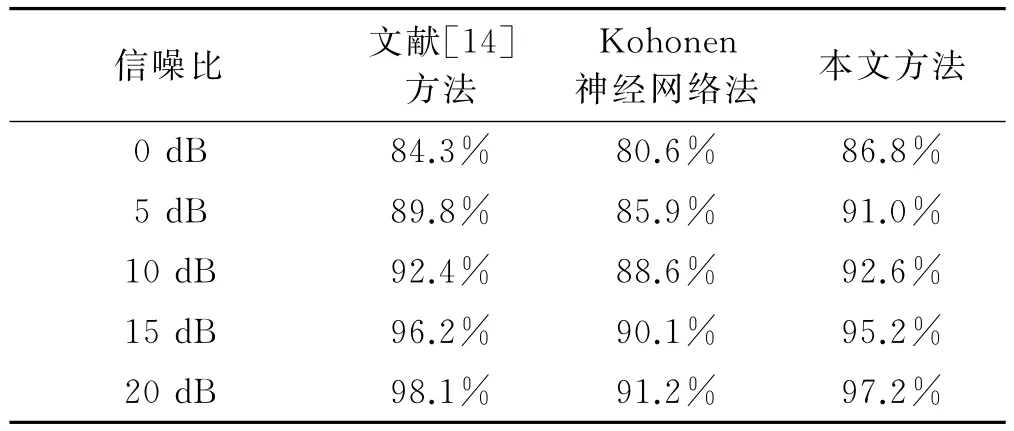
表1 不同方法的信号分选正确率

4 结束语

稳定、可靠的脉内参数是解决当前雷达信号分选困难的有效参数之一。但是常用方法在利用脉内参数时较为单一，仅把脉内参数作为辅助分选的参数，导致脉内参数利用率不高。本文研究基于脉内多参数对信号分选结果的影响，提取相像系数和高阶累积量，采用改进的支持向量机，对雷达信号辐射源进行分选，仿真结果验证了基于脉内多参数进行信号分选的可行性。文章的不足之处在于，由于是方法可行性验证，所以仿真条件设置简单、实验验证不够充分、脉内参数的提取和选择存在主观因素的影响。下一步将重点研究如何从脉内特征参数中选取最佳的脉内特征参数子集。■

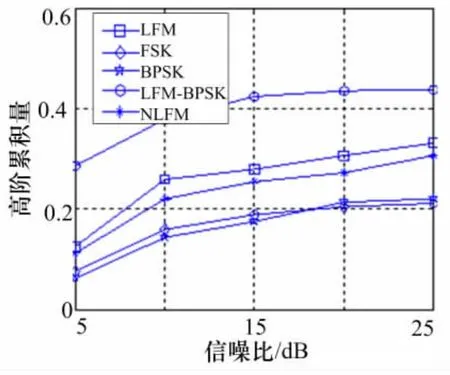
图5 高阶累积量F2

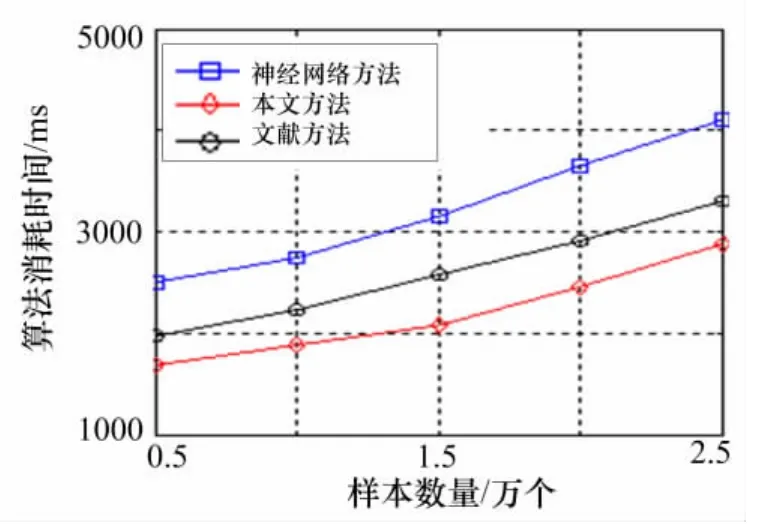
图6 三种方法的时间复杂度