从能量守恒的角度看雷达相参压制干扰的相参得益

李 宏，薛 冰，赵艳丽

（中国洛阳电子装备试验中心，河南 洛阳471003）

0 引言

自雷达相参压制干扰技术提出以来，学术界各种新型相参干扰产生技术尤其是时序控制技术以令人目不暇接之势迅猛发展。干扰机设计师们则把学术界提出的各种相参干扰产生技术在实际的干扰机上予以实现，变成产品，推动相参干扰技术的应用发展。作为干扰机综合性能的检验者，电子装备试验中心的试验师们在对干扰机进行性能检验时，针对检验过程中出现的各种现象和暴露出的各种问题开展研究为干扰技术的改进完善提出各种有益的建议，同时也推动了干扰技术的发展［1－4］。现在雷达相参压制干扰技术已经替代了传统的噪声压制干扰，成为现代雷达压制干扰技术的首选。

1 相参压制干扰的问题

自雷达相参压制干扰技术提出以来，几乎一直延续至今的一个普遍的共识是：由于相参压制干扰是对被干扰雷达信号的实际采样和不失真的存储转发，其与雷达信号是完全相参的，因而能够获得雷达信号处理的全部相参得益，包括脉冲压缩得益和相参积累得益。首先，一个存储转发的假目标干扰信号在经过被干扰雷达的信号处理系统处理后，由于其与雷达脉冲压缩处理匹配滤波器完全匹配，因而能够得到其全部脉冲压缩得益；其次，由于假目标脉冲是干扰机对雷达信号不失真地采样并存储在数字射频存储器（DRFM）中后转发的，因而不同雷达周期对应的假目标脉冲串是相参的，所以这些脉冲串应该能够获得雷达信号处理后的相参积累得益。但实际情况如何，由下面这个实例进行说明。

某型相参压制雷达干扰机挂飞试验中，其试验态势如图1所示。

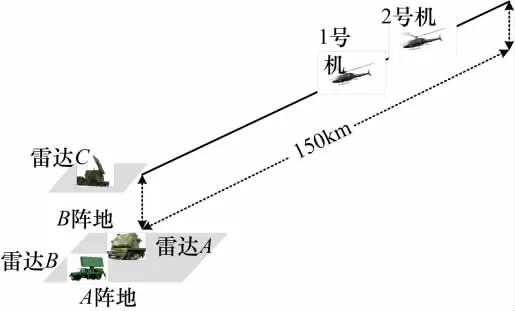
图1 某型雷达相参压制干扰机挂飞试验态势图

从图1中可以看出，干扰态势为随队干扰，2架飞机编队飞行，1部被试雷达相参压制干扰机搭载在前机上，掩护后机突防，采取1部干扰机同时对3部雷达进行干扰的多目标干扰模式。对于欲干扰的某一部具体雷达（如雷达A）来说，如果要求干扰机将目标飞机掩护至距该雷达50km处，则对干扰机的有效辐射功率需求是多少？

通过该雷达的工作模式、状态和参数可以计算得到，其脉冲压缩得益为30dB，相参积累得益为12dB，则总的相参处理得益为42dB。若采用传统的噪声压制干扰，则通过经典的干扰方程［5］可以计算出干扰机的有效辐射功率需求为22dBW（150W）；若采用相参压制干扰，具体采用占空比为1∶1的间歇采样干扰样式，假设按照雷达对抗业界普遍的观点，干扰信号能够获得雷达信号处理的全部相参得益的话（当然，需要扣除极化失配损失以及间歇采样占空比带来的损失等各种其他损失），则在理论上，可以计算出干扰机的有效辐射功率需求为－17dBW（0.02W）。所以，理论上，当干扰机采用相参压制干扰时，若能够获得雷达信号处理的全部相参处理得益，则有效辐射功率只需要达到－17dBW，就可以将目标飞机掩护至距离雷达A 50km处。然而实际上，试验中的干扰机设计功率为2W（3dBW），比理论上需要的干扰功率值高出足足20dB，可以说留出了足够的功率富余，而试验结果却是不满足掩护距离的指标要求。为此，干扰机设计师对干扰机进行了功率提升，将其有效辐射功率从2W提高至22W（13.4dBW），重新试验，结果刚好满足指标要求。

另外，近些年来进行的数十次雷达对抗试验结果都表明，如果雷达相参压制干扰能够获得雷达信号处理的全部相参得益的理论成立的话，则所有的试验结果都与用雷达干扰方程计算出来的干扰机功率需求不相符合。

仔细分析理论与实际不相符合的原因，一是雷达干扰方程不正确；二是相参压制干扰能够获得雷达信号处理全部相参处理得益的理论不正确。

文献［6］从理论上分析论证了雷达相参压制干扰能够获得欲干扰雷达信号处理的全部相参得益的理论不成立的原因，并且从雷达恒虚警（CFAR）检测［7］的角度，定量计算了相参压制干扰通过雷达信号处理后最终的脉冲压缩处理得益。结果表明，相参压制干扰的单个假目标信号在经过雷达脉冲压缩处理后，确实可以得到其脉冲压缩得益，但是在经过雷达恒虚警处理后，相参压制干扰总的脉冲压缩得益又被抵消，最终脉冲压缩得益为零甚至为负。本文力图从另外一个角度——能量守恒的角度来分析相参压制干扰通过雷达信号处理后最终的脉冲压缩得益。

2 从能量守恒角度分析雷达相参干扰相参得益

相参干扰对雷达进行压制，本质上仍是属于能量域的对抗，即干扰信号试图从能量上压制住真目标回波，使得被干扰雷达不能从干扰信号环境中把目标回波信号检测出来。因此，从能量域的角度，以能量守恒与转化定律来进行分析。

2.1 脉冲压缩得益

由雷达原理［8］可知，雷达对目标的检测，是在背景噪声中检测目标的回波信号；雷达对目标的探测能力，本质上取决于回波信号相对于背景噪声的能量大小。而能量等于功率乘以时间，所以，当一部雷达的功率孔径积确定以后，提高其探测能力最有效的方法之一就是尽量增大其发射脉冲的宽度，因为在雷达天线增益和发射的脉冲功率确定以后，脉冲宽度越宽，每个脉冲的能量就越大，雷达进行单脉冲检测的探测威力就越大，这也是现代雷达普遍采用大时宽带宽积信号的根本原因。干扰机对雷达的压制，本质上就是跟目标回波信号拼能量，使得雷达不能将目标回波信号从干扰背景下检测出来。当干扰机的等效辐射功率（Pj）确定以后，其能量（Qj）也是等于功率乘以时间。由于功率一定，则时间越长，能量就越大。对于一部具体的雷达来说，干扰信号对一个目标回波信号的有效压制时间就是该雷达脉冲信号的宽度τ，因此，干扰机对该回波信号的压制能量Qj＝Pjτ。由于对一部确定的雷达来说，干扰功率Pj和干扰时间τ（即雷达的脉冲宽度）都是确定的，因此，干扰能量Qj也是确定的。那么，根据能量守恒定律，干扰机的干扰能力也是确定的，不会因为干扰信号是否能够获得雷达脉冲压缩得益而改变。脉冲压缩前后一个脉冲信号的功率-时间关系如图2所示。

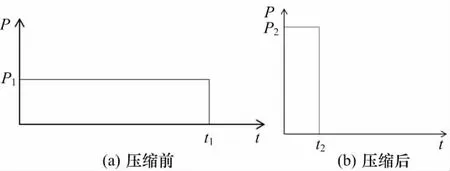
图2 脉冲压缩前后一个脉冲信号的功率-时间关系图

图2 （a）为雷达脉冲压缩之前的一个假目标脉冲，图2（b）为该假目标脉冲经雷达脉冲压缩以后的情况，脉冲压缩之前该假目标脉冲的能量为Q1＝P1t1，脉冲压缩之后的能量为Q2＝P2t2。由于雷达脉冲压缩处理是一个无源过程，即没有能量输入，那么，根据能量守恒定律，脉冲压缩前后该脉冲的能量是不变的，因此有Q1＝Q2。脉冲压缩的得益使得假目标的功率由P1升至P2，但干扰覆盖的时间相应地由t1降至t2，且存在关系：

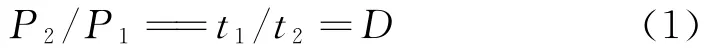
式中，D为脉冲压缩得益，等于雷达脉冲信号的带宽B乘以时宽τ，即D＝Bτ。

如果单纯从雷达脉冲压缩这个节点来看，相参压制干扰的假目标信号能获得雷达信号处理的脉冲压缩功率得益。假目标信号获得了脉冲压缩的功率得益，但失去的是时间覆盖范围，而且由式（1）可知，假目标信号通过脉冲压缩所获得的功率得益与其时间覆盖范围的损失是相等的。

根据脉冲压缩的原理可知，脉冲压缩处理是把一个功率较低的宽脉冲压缩成一个功率较高的窄脉冲。根据雷达CFAR处理的原理［7］可知，其通过单元平均，将落入其某个处理单元的假目标功率平均分配到各个恒虚警处理单元中去，恢复到了脉冲压缩之前的状态，如图3所示。

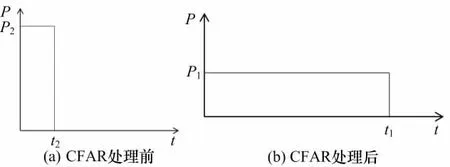
图3 雷达CFAR处理前后假目标信号的功率-时间关系图

所以，雷达CFAR处理是把又高又瘦的图3（a）中的假目标脉冲打压成了又矮又肥的图3（b）中的脉冲，假目标信号又回到了原形，因此从最终的效果来说，相当于没有了脉冲压缩得益。

总之，能量是守恒的，在没有外部能量输入的情况下，系统内不可能无缘无故生出新的能量来。由于雷达信号处理是一个无源过程，没有能量的输入，因此，在雷达信号处理前后，相参压制干扰的假目标能量是固定的，要在功率上增加，只有牺牲时间上的覆盖范围。而时间上的覆盖范围又是必须满足的，为了保证时间上的覆盖，功率就不可能增加，这是雷达相参压制干扰最终没有脉冲压缩得益的根本原因。

实际上，从雷达方程也可以得到此结论。雷达方程有几种不同的形式，其中常用的有功率形式和能量形式。如果从功率形式的雷达方程去理解，很容易陷入“雷达相参压制干扰可以获得雷达信号处理脉冲压缩得益”的陷阱；如果从能量形式的雷达方程去理解，就会明白雷达相参压制干扰的能量是固定的，因而其干扰能力也是固定的，不会因为雷达信号处理的脉冲压缩而提高其干扰能力。

2.2 相参积累得益

雷达相参压制干扰由于是对雷达信号不失真地采样存储后再转发，各雷达重复周期对应的假目标脉冲信号之间是相参的，因此与目标回波信号一样，可以获得雷达信号处理的全部相参积累得益。如假设雷达动目标检测（MTD）进行16点FFT处理，则可以获得最大12dB的相参积累得益；当雷达MTD进行64点FFT处理时，则可以获得约18dB的相参积累得益。这在很多应用场合，是一笔可观的得益。

从能量守恒的角度可以解释相参压制干扰能获得雷达信号处理的相参积累得益问题。

对于相参雷达来说，由于其发射的脉冲串是相参的，通过将不同雷达周期内同一目标的回波信号进行相位对准，可以将接收到的同一目标的回波信号串进行相参积累，其效果相当于把这一串脉冲一个挨着一个排在一起，实际上可以看成增大了回波信号脉冲的宽度，从而提高了回波信号的能量。如假设一个脉冲的宽度为τ，雷达对32个脉冲进行相参积累，可以看成把这32个宽度为τ脉冲排列在一起组成一个宽度为32τ的新脉冲，这样，在脉冲功率不变的情况下，新脉冲比原脉冲的能量增大了32倍，这32倍得益就是相参积累的得益。

2.3 小结

通过前面的分析，相参压制干扰通过雷达信号处理过程中所获得的得益情况如图4所示。

图4 相参压制干扰通过雷达信号处理过程的得益情况

每一个相参压制干扰的假目标脉冲在通过雷达信号处理的脉冲压缩处理后，其与脉冲压缩处理的匹配滤波器是完全匹配的，将会获得脉冲压缩得益。然后假目标串在经过MTI／MTD处理后，将会获得相参积累得益。最后在经过雷达CFAR处理后，又会失去脉冲压缩得益，只剩下相参积累得益。这就是相参压制干扰通过雷达信号处理过程中所获得的得益变化情况。

3 实例验证

回到第1节的例子。如果按照相参压制干扰能够获得雷达信号处理的全部相参处理得益进行计算，则可得到对干扰机的有效辐射功率需求为－17dBW（0.02W），但实际上当干扰机功率提高到13.4dBW（22W）时，刚好达到压制距离的指标要求（指标要求50km，实际试验结果为49.3km）。

根据雷达参数，其脉冲压缩得益为30dB，相参积累得益为12dB，如果扣掉脉冲压缩得益，则理论计算得到相参干扰下对干扰机的有效辐射功率需求为13 dBW（20W），与实际情况13.4dBW（22W）吻合。

实践反复证明，如果扣掉脉冲压缩得益，只考虑相参积累得益，则对相参压制干扰功率需求的理论计算结果跟历次实际试验结果是吻合的。

4 结束语

雷达相参压制干扰技术自从提出并在实际中得到应用以来，其能够获得雷达信号处理的全部脉冲压缩得益和相参积累得益已是共识。在实践中发现这一认识的理论跟实践不符，并且差距很大，往往达到几十个分贝，这不是因为干扰机工艺水平不够所导致，也不是因为干扰算法不够精细或者时序设计不够合理所致。由此分析原因，只有可能是雷达相参压制干扰能够获得雷达信号处理的包括脉冲压缩得益和相参积累得益在内的全部相参处理得益的认识不正确。为此，本文从能量域的角度，运用能量守恒与转化定律进行分析，得到了雷达相参压制干扰只能获得雷达信号处理的相参积累得益而不能获得脉冲压缩得益的结论，并以实际情况为例，印证了本文结论的正确性。■