基于六自由度非线性模型的稳定储备计算方法

张羽白，崔彦勇，李玉飞，刘宝文，相 梅，杨振声

（航空工业洪都，江西 南昌，330024）

0 引言

高机动能力是现代战机的重要特征，而飞机的机动响应能力与稳定性是一对矛盾，在飞机气动平台确定后，电传飞机的稳定性能主要取决于控制律设计。为尽可能提高飞机机动能力，需要在设计阶段准确地计算飞控系统的稳定裕度，为控制律设计提供明确的稳定边界。

其中，稳定储备是评价飞机和飞控系统稳定性的一个重要指标，表明系统稳定的可靠程度。稳定储备包括幅值储备和相位储备，即系统进入不稳定状态之前可以增加的相位和增益变化，相位储备和幅值储备越大，系统越稳定，GJB 2191中对其有明确指标要求。

在控制律设计阶段，稳定储备理论计算利用线性化小扰动模型和飞行控制系统线性化模型求取系统稳定储备，但通过后期和铁鸟试验得到的稳定储备对比发现，该方法存在以下问题：采用小扰动模型并线性化的方法，忽略了飞机气动特性及飞控系统存在的多种复杂非线性，所求取的稳定储备与实际稳定储备存在较大偏差，可能导致后期控制律设计反复。

基于以上原因，本文提出一种基于六自由度非线性模型的稳定储备理论计算方法，通过快速傅里叶变换方法计算飞控系统纵、横、航向的稳定储备。

1 六自由度非线性模型下的稳定储备计算方法

根据快速傅里叶变换建立六自由度非线性模型的稳定储备计算模型。

1.1 快速傅里叶变换

对于一个周期连续信号f（t）可以通过傅里叶级数将其分解成不同频率的正余弦函数之和，从频率的角度对信号进行分析和研究，如式1～6所示。

其中，ω1、T1分别是原周期函数的角频率和周期。

对这种频域分析的概念进行拓宽，可以得到时域信号非周期甚至是离散情况下对应的傅里叶变换方法。工程应用一般使用数字计算机进行计算，要求输入的时域信号和输出的频域信号都是离散信号，且输入的时域信号一般为非周期，这种情况下应采取离散傅里叶变换方法，如公式7～9所示：

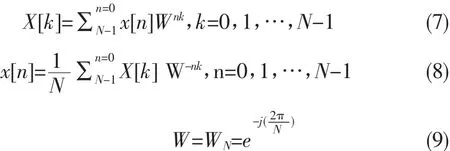
通过离散傅里叶变换，可以将离散的时域信号和频域信号进行相互转换，同时，输入输出信号都是数字信号，这使得该过程可以使用数字计算机进行，拓展了该方法的实用性。

然而，根据式（7）和式（8），整个离散傅里叶变换运算需要4N2次实数乘法和2N（2N-1）次实数加法，计算复杂度为o（N2）。如果直接用定义式计算离散傅里叶变换，随着信号长度的增加，计算复杂度会急速增加，运算量非常大。

因此，直接计算离散傅里叶变换的方法是行不通的，必须寻找减少运算次数的途径，由此催生了快速傅里叶变换算法（FFT）。

快速傅里叶变换算法主要有两大类，即时域抽取法和频域抽取法，又分别被称为库利算法和图基算法。这两种算法分别按照时域和频域的奇偶性对序列进行分解，从而减小了计算复杂度，具体做法本文不做赘述。当序列长度为N=2M时，其计算复杂度为o（Nlog2M）。N越大，快速傅里叶变换相对于原始离散傅里叶变换速度越快，这样就大大提升了离散傅里叶变换的实用性。

1.2 稳定储备计算方法

基于六自由度非线性模型的稳定储备原理图见图1和图2，其中δio为扫频信号，δz为输入时域信号，X为输出时域信号。

稳定储备计算方法具体步骤如下：

1）在飞机配平状态下，从作动器模型后加入扫频信号，选取合适的起始频率、终止频率，采样信号长度为系统开始接收扫频信号扰动到系统响应稳定的时间长度。

2）根据采集的输入、输出时域信号，使用快速傅里叶变换将其变换为频域信号；将输出信号对应的频域信号除以输入信号对应的频域信号，即可得到系统本身的频域特性曲线，这些频域信号值都是复数，可以方便地求出幅值和相位。频域信号对应的频率值根据式10求取。

图1 纵向稳定储备计算原理图

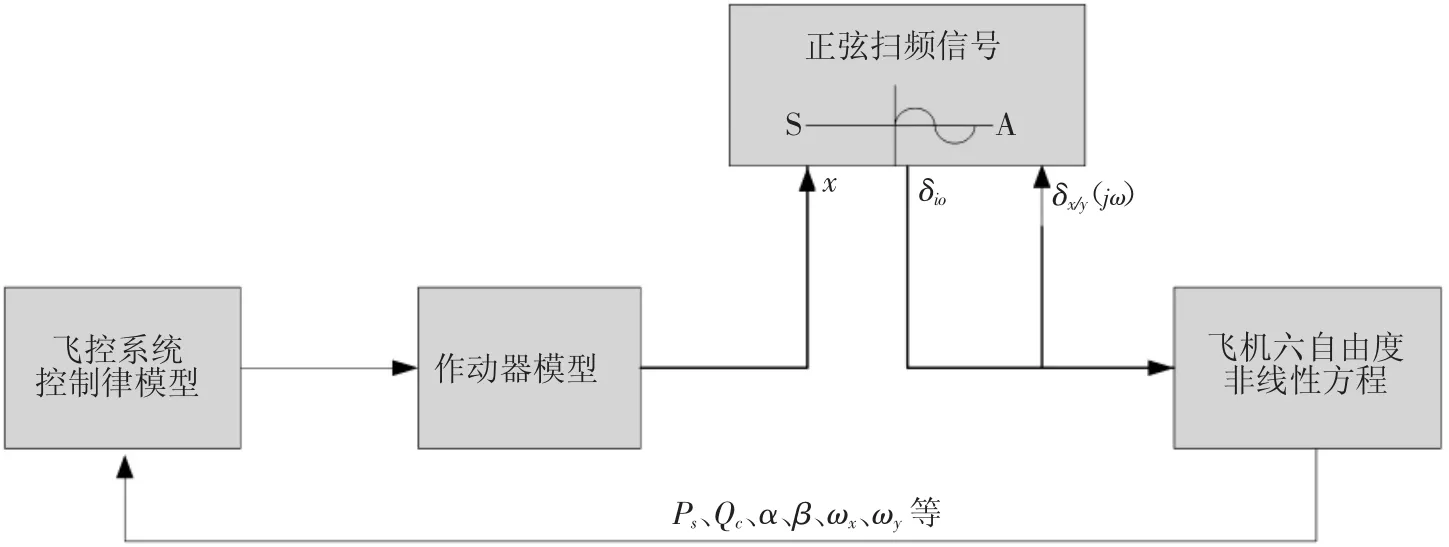
图2 横、航向稳定储备计算原理图

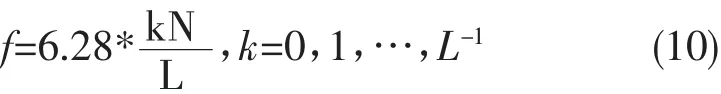
其中，N=100，表示时域信号采样频率，L表示采样计算得到的频域信号总数，例如，当采样时间为10s时，L=1001；系数6.28是将频率单位由HZ转换为rad/s，以便与试验结果进行比较。得到频域信号幅值、相位和对应频率以后，即可绘制伯德图求取稳定储备。

2 六自由度Simulink模型稳定储备仿真计算

以纵向稳定储备求取为例，搭建六自由度非线性模型，扫频模块位于作动器后，如图3所示。

按照2节所述方法步骤，绘制伯德图如图4所示：

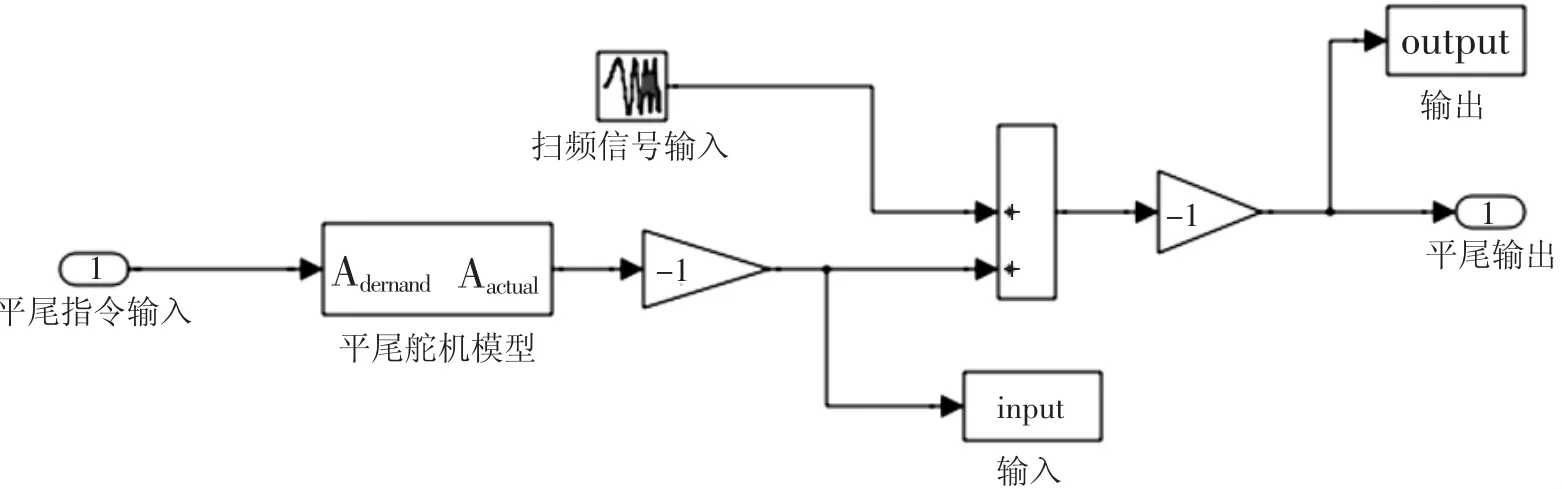
图3 纵向扫频模块示意图

图4 起飞0km、0.2M非线性稳定储备伯德图

通过伯德图，可以计算出系统的幅值稳定储备和相位稳定储备。如图4，在幅值频率特性图中可以算出穿越0db频率为2.82rad/s，根据相位频率特性图可知该频率下对应的相角为-104.22°，系统相位储备GM=-104.22°-（-180°）=75.78°；同理，根据相位频率特性图可以计算出系统相位-180°时对应的频率为19.37rad/s，对应的系统幅值稳定储备PM=18.50db。这样就得到了表征系统稳定程度所需的稳定储备所有参数。

3 结果对比分析

将基于六自由度非线性模型稳定储备计算方法得到的计算结果与小扰动方法、铁鸟台试验方法得到的结果进行对比分析。

以某型飞机为原型，搭建六自由度非线性仿真模型，选取合适状态点，按照第2节所述方法步骤进行仿真计算纵向稳定储备，对应构型对应状态点的铁鸟稳定储备试验结果和小扰动模型仿真计算结果对比见表1。

表1 三轴稳定储备对比

从表1可以看出，通过六自由度非线性模型稳定储备计算方法计算出来的纵向稳定储备，相对于原有的小扰动模型计算方法，更接近真实铁鸟试验结果，但还存在一定差异。

分析认为，误差存在的原因可能是真实铁鸟环境各环节的时延和相位滞后相对于理想仿真模型更大，导致在真实铁鸟试验得到的伯德图中，系统幅值响应与理想六自由度模型一致，穿越频率相同，而系统相位下降相对更快，穿越频率对应的相位距离-180°更近，因此相位储备更小；同理，真实铁鸟试验系统相位更快到达-180°，导致相角-180°处频率更小，从而幅值储备也更小；也有可能是铁鸟试验和非线性仿真方法不同扫频方法造成的，有待进一步研究。

4 结语

本文以某型飞机为原型机，运用快速傅里叶变换方法在六自由度非线性模型中进行飞机稳定储备计算。通过仿真结果对比分析，验证了非线性模型稳定储备计算方法在纵、横、航向稳定储备求取上的准确性，总体上优于原有的小扰动模型稳定储备计算方法，能够减少控制律设计的迭代次数，提高工作效率。