变厚度板中Lamb波传播的模态转换特性

，，，

(湖南科技大学 机械设备健康维护重点实验室，湘潭 411201)

Lamb波技术以其传播距离远及对缺陷的高敏感性，广泛应用于大面积板类结构的缺陷检测中。利用Lamb波与缺陷界面作用产生的散射信号，通过信号分析与特征提取可以对缺陷信息进行识别。工程结构中大量采用变厚度板来减轻结构重量和优化结构力学性能，常见的厚度变化过渡结构包括阶梯型、斜面型和圆弧型，如风力机叶片、飞机机身、直升机机翼、舰船壳体等。类似于含小缺陷平板中的Lamb波传播特性[1-6]，非对称变厚度板中的Lamb波将产生复杂的频散和模态转换现象，增大变厚度板缺陷识别的难度。因此，研究Lamb波在变厚度板中的传播特性，掌握板厚变化量对Lamb波传播特性的影响，是变厚度板缺陷检测必须首先解决的关键问题。

目前国内外对含缺陷平板中的Lamb波传播特性分析较多，但对变厚度板中Lamb波频散和模态转换特性的研究尚不充分。EL-KETTANI和PREDOI等[7-8]研究了小角度斜面型变厚度板S0模态频散特性随频厚积变化及模态转换的情况，团队中MARICAL等[9]进一步地讨论了厚度呈高斯曲线变化时模态转换后A0和S0能量与激励频率的关系。JENOT等[10]简要地分析了厚度变化量对A0模态传播速度的影响；NURMALIA等[11]讨论了SH0波在线性变厚度板中的模态转换特性。针对风力机叶片T型结构和直升机旋翼I型结构，RAMADAS等[12-13]分别开展了A0和S0模态转换特性分析。国内尚世同等[14]较早地探讨了Lamb波用于变厚度发动机叶片的裂纹检测；田光春等[15-16]分析了台阶型和斜面型变厚度板中模态转换后A0、S0和A1反射系数和透射系数随厚度的变化情况；李喜朋[17]较全面地讨论了变厚度板Lamb波传播特性及其缺陷检测方法。

针对工程结构中变厚度板常见的阶梯型、斜面型和圆弧型过渡结构，定义倾斜角/弦切角为基本变量，采用有限元软件ANSYS分析了低阶单一A0模态激励下的模态转换特性，探索了模态转换后A0和S0反射系数和透射系数随倾斜角/弦切角变化的规律。论文能为工程实际中变厚度板Lamb波散射信号的分析提供理论依据，有利于提高变厚度板中缺陷检测的准确度。

1 变厚度板有限元仿真模型的建立

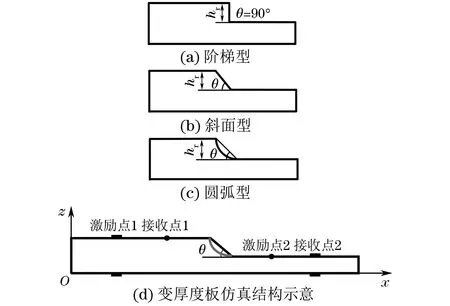
图1 变厚度板过渡结构示意

变厚度板过渡结构的阶梯型、斜面型和圆弧型结构示意如图1所示，变厚度主要参数为厚度差hr和倾斜角/弦切角θ。

阶梯型变厚度板可以看成倾斜角为90°的斜面型板结构。圆弧型过渡段始终保持与薄端板相切，当弦切角等于45°时，过渡圆弧半径等于厚度差hr，大于4°时过渡结构为圆弧-直角混合结构，故不讨论弦切角大于45°的情况。以某风力机叶片前缘翼面变厚度板类结构为分析对象，厚端厚度为10 mm，薄端厚度为5 mm，厚度差hr为5 mm，假定倾斜角θ变化范围为10°～90°，圆弧型弦切角θ变化范围为10°～45°。为了分离板端反射信号的影响，仿真分析的变厚度板长为4 m。

将变厚度板视为无限大自由薄板，Lamb波传播特性分析仅需建立二维截面模型。采用ANSYS软件中的Plane 182单元建立变厚度板截面的有限元分析模型(见图2)。变厚度板为复合材料板，不考虑材料各向异性，假定材料密度为1 990 kg·m-3，弹性模量为44.68 GPa，泊松比为0.28。

图2 有限元网格模型

图3 群速度频散曲线

变厚度板缺陷检测采用低阶单一模态激励来减少缺陷散射信号的复杂度，考虑到A0波速慢且波长短，适于检测复合材料内部细微缺陷，通过在变厚度板上下表面加载同向激励来实现单一低阶A0模态激励。计算得到的变厚度板频散曲线如图3所示，因此激励频率选为50 kHz和100 kHz，以避免产生高阶模态，对应的A0模态和S0模态的群速度如表1所示。A0模态激励波形为汉宁窗调制的五周正弦波(见图4)。

图4 50 kHz激励波形

表1 基本Lamb波的群速度 m·s-1

为了保证Lamb波传播特性分析结果的准确性，单元网格尺寸小于激励频率最大时对应波长的1/10[18]，ANSYS瞬态动力学分析积分步长必须小于激励频率最大时对应周期的1/20。不考虑阻尼引起的衰减，ANSYS模型网格尺寸为1 mm，积分步长设为5×10-7s。

现有文献研究表明[5]：Lamb波在非对称变厚度界面不仅发生了反射和透射，还将发生模态转换。忽略结构阻尼，定义反射和透射的A0和S0模态与激励A0模态的幅值比来表征厚度变化界面产生的反射、透射和模态转换特性。透射系数定义为

(1)

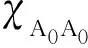
同理，反射系数定义为

(2)

2 变厚度板模态转换特性与结果分析

2.1 变厚度界面处Lamb波模态转换现象

图5 A0和S0模态截面的归一化位移曲线

厚端激励频率为100 kHz时，A0和S0模态截面的归一化位移曲线如图5所示，由图5可以看出，S0模态的面内位移较大，离面位移较小，A0模态面内和离面位移均较大。由于激励频率为50 kHz时的截面位移情况相同，后续结果均只列出面内x方向的位移响应曲线。

通过ANSYS瞬态动力学分析可获得变厚度板的位移响应曲线。A0激励施加位置如图1(d)所示，激励点1和2分别位于厚端和薄端的1 m和3 m位置，接收点1和2分别为厚端和薄端的1.5 m和2.5 m位置。斜面型变厚度板倾斜角为50°时，在厚端激励点1处施加100 kHz的A0激励，2个接收点x方向位移响应曲线如图6，7所示。

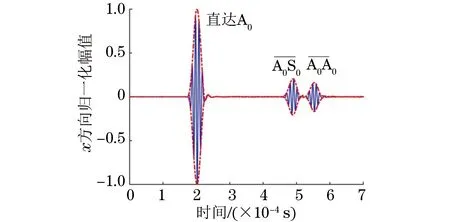
图6 激励A0模态的反射波

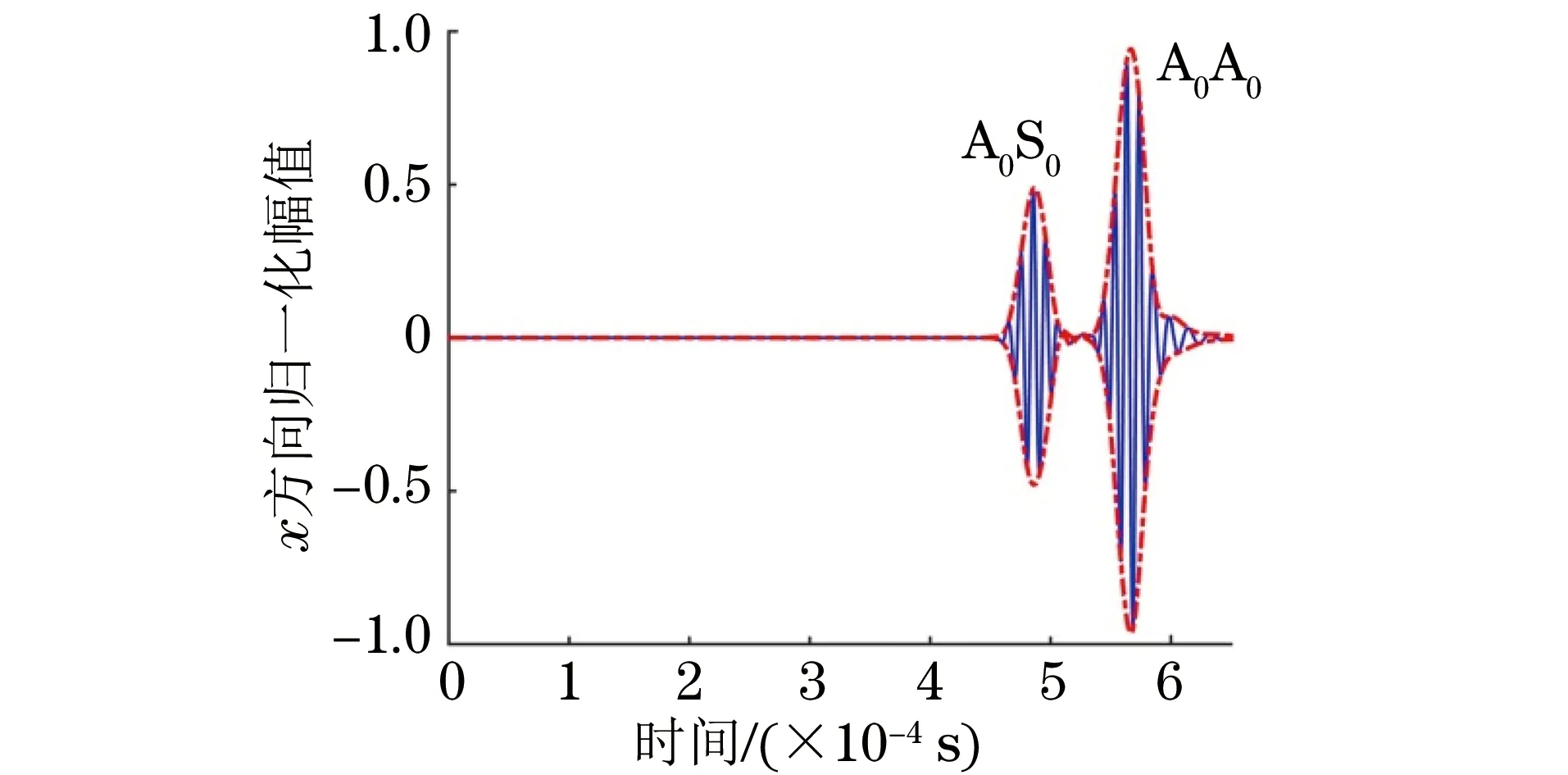
图7 激励A0模态的透射波

根据图6，7以及表1 中A0和S0模态的群速度，可以得出：

(1) 由于变厚度界面处A0模态发生模态转换，反射波和透射波中均含有A0和 S0两种模态，S0模态相比A0模态传播速度快，故出现时间早。

(2) 图7中透射A0模态时域波形发生变化，由激励点的5周正弦波变为7周正弦波，这是由A0模态的频散效应造成的。

(3) 激励A0模态在变厚度界面处模态转换后产生A0和S0模态，使缺陷散射信号更加复杂，准确区分变厚度和缺陷界面散射信号是提高缺陷识别准确度的关键。

2.2 斜面型变厚度板结构的模态转换特性

通过提取斜面型变厚度板A0和S0模态的波包幅值，厚端和薄端A0模态激励下的A0和S0反射系数和散射系数随倾斜角的变化关系如图8，9所示。

图8 厚端A0模态激励的反射系数和透射系数

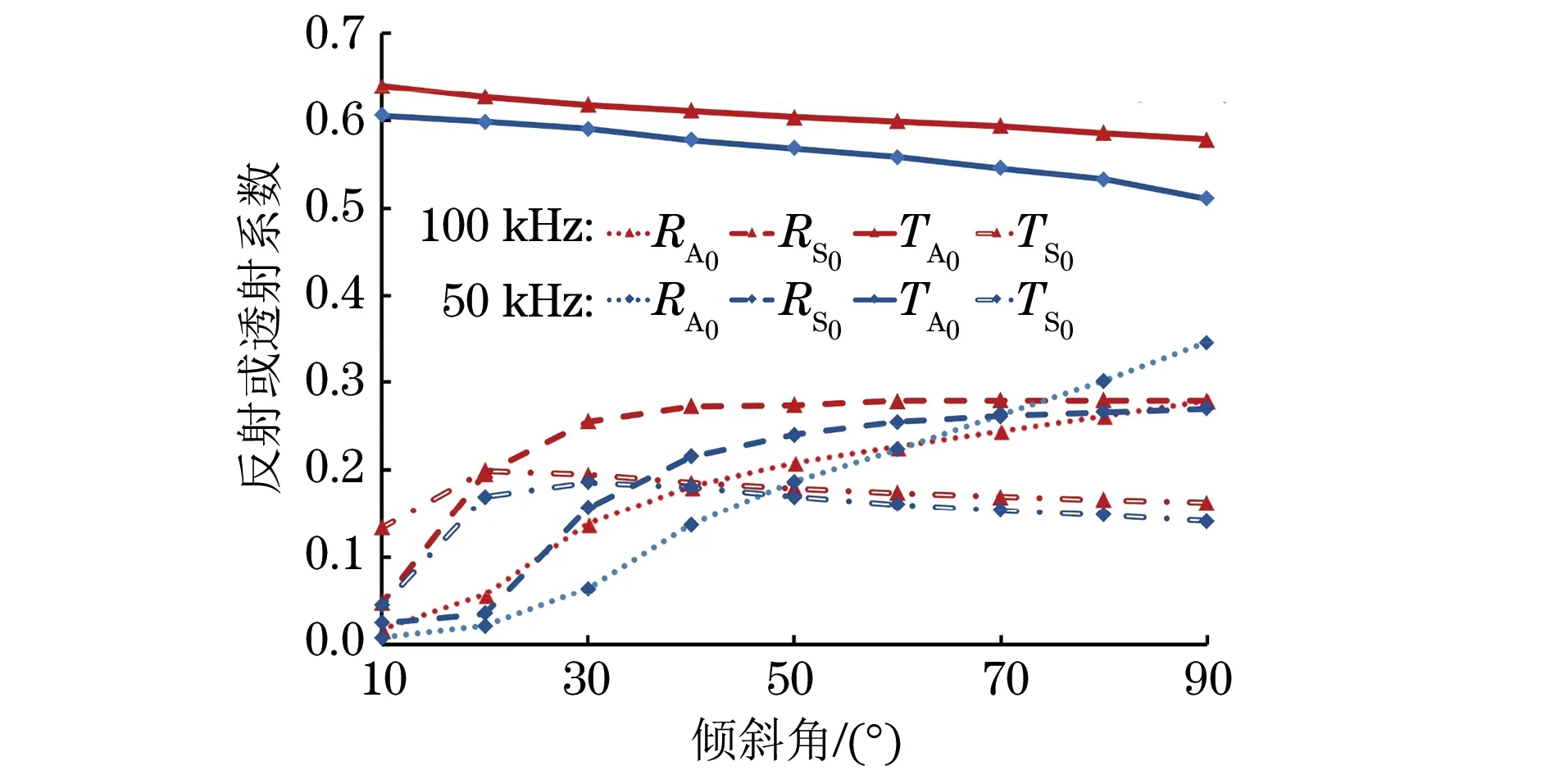
图9 薄端A0模态激励的反射系数和透射系数

(1) 随着倾斜角的增大， A0模态透射系数TA0递减，模态转换产生的S0模态透射系数TS0增加，且其幅值先增加得快，后来变得平缓。这表明随着倾斜角度的增加，激励波A0模态发生模态转换产生的S0模态的信号增强，透射A0模态的信号减弱。

(2) 反射系数RA0和RS0随着倾斜角的增大而增大，也呈现出增加幅度先较大而后变得平缓的趋势。这表明激励波A0模态在变厚度界面且倾斜角较大时的反射较大、透射较小，这也符合波的反射和折射定律。

(3) 在厚端激励时，由于激励A0传播时其板截面积变小，波的幅值将增加，故倾斜角较小时(<20°)其透射系数大于1。相反地，薄端激励时，激励A0模态幅值将降低，透射系数远小于1。

(4) 50 kHz和100 kHz两种激励频率下，透射系数和反射系数变化趋势一致。但由于两种频率下A0模态的波长不同，影响着A0模态的透射、反射及模态转换特性，透射和反射系数存在一定的差值。

2.3 圆弧型变厚度板结构的模态转换特性

变厚度板圆弧型过渡相比斜面型过渡更能够减轻板结构的质量，风力机叶片前后翼缘变厚度处广泛采用圆弧型过渡。厚端激励和薄端激励下A0激励模态的反射系数和透射系数随着倾斜角/弦切角的变化曲线如图10，11所示，其激励频率为50 kHz。

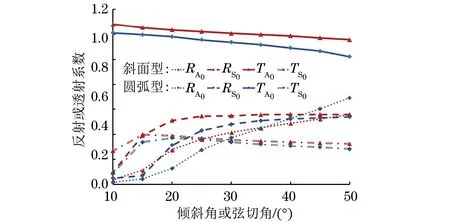
图10 厚端激励下斜面/圆弧型变厚度板的反射系数和透射系数随倾斜角/弦切角的变化曲线

图11 薄端激励下斜面/弧线形变厚度板的反射系数和透射系数随倾斜角/弦切角的变化曲线

从图10，11可以看出，圆弧型和斜面型两种变厚度板结构的模态转换特性存在差异。倾斜角/弦切角较小时，反射系数和透射系数的差值较大。随着角度的增大，差值逐渐减小；在厚端激励和薄端激励两种情况下，两种过渡结构中A0模型的反射系数和透射系数变化趋势一致。

3 结论

针对工程实际常见的阶梯型、斜面型和圆弧型变厚度板结构，采用有限元软件ANSYS开展了Lamb波传播响应分析，研究了激励A0模态转换后，A0和S0反射系数和透射系数随倾斜角/弦切角变化的规律，能为准确区分变厚度和缺陷界面的散射信号提供理论依据，有利于提高变厚度板中缺陷识别的准确度。

(1) Lamb波在变厚度板结构中存在明显的模态转换现象，且随着倾斜角/弦切角的增加，A0模态转换产生的透射和反射S0幅值随之增大。

(2) 随着倾斜角/弦切角的变大，A0模态的反射增强，反射系数随之增大，A0模态透射系数逐渐减小。

(3) 在50 kHz和100 kHz两种激励频率下，A0模态反射系数和透射系数变化趋势一致，但由于波长不同造成相应系数存在一定的差值。

(4) 厚端激励和薄端激励下，由于A0模态传播时截面积发生变化，小倾斜角/弦切角时A0模态透射系数分别大于和小于1；圆弧型和斜面型变厚度结构的反射系数和透射系数存在一定的差值。