电磁超声检测各向同性金属材料的弹性模量及声波模式转换
2018-11-29,,
,,
(苏州博昇科技有限公司, 苏州 215123)
弹性模量是材料非常重要的参数,关系到材料抵抗外界作用力而引起变形的能力,以及使用过程中是否容易出现疲劳损伤等,对其进行快速、方便和准确地测量和评价意义重大。弹性模量传统的检测方法包括静态法、动态法和超声波法。静态法有国家标准,主要依据材料在弹性拉伸时应力和应变的线性关系来测试,但检测结果易受检测过程和外界因素的影响;动态法是通过寻找材料的共振频率来进行测试,但共振频率依赖操作人员主观判断的程度较高,寻找困难,操作复杂。
超声波法主要是通过测量材料中至少两个模式的超声波声速,比如纵波和横波、纵波和表面波、横波和表面波的传播速度来推算材料的弹性模量。这种方法适用范围广,测量方式简单;压电超声波法受限于耦合剂的耦合效果,重复性较差,声速的检测精度存在不确定性;电磁超声波检测(EMAT)法不需要耦合剂,材料表面可以有油漆、腐蚀和凹凸不平,相比压电超声波法,其重复性好,检测精度更高。但电磁超声波的激发原理决定着电磁超声波不容易产生纵波,模式转换效率低,限制了其在材料弹性模量检测领域的应用。
徐春广等[1-2]利用压电超声激发纵波和横波检测螺栓拉应力。DING等[3]研究了电磁超声波激发横波及横波模式转换纵波测量螺栓应力。任洁等[4]研究了超声波弹性模量的测试系统。
笔者借助大功率超声检测仪PREMAT-HS200,通过激发电磁超声换能器获得超声横波、纵波和模式转换的纵波和横波。接收信号的信噪比优异,除横波外,纵波和模式转换波也清晰可见。通过分析波包最大幅值和时间,达到了利用电磁超声波法快速、准确、简单、有效地检测材料的杨氏模量和泊松系数的目的。
1 基本原理
各向同性金属材料的弹性模量E和泊松系数ν与纵波声速CL和横波声速CT的关系[5]为
(1)
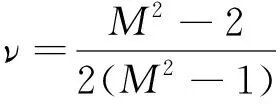
(2)
式中:M=CL/CT,为材料的纵波声速与横波声速的比值;ρ为材料密度。
如果能确定材料密度ρ,横波声速CT以及纵波与横波声速的比值M,就很容易计算出材料的杨氏模量和泊松系数。
电磁超声换能器激发超声波入射至工件表面时,可以认为有两个独立的通道同时在工件表面产生纵波和横波。由于电磁超声波的接收是发射的逆效应,所以电磁超声波对纵波的接收效率要远远低于对横波的接收效率。定义电磁超声换能器对纵波和横波的接收效率比值为γ,即仪器屏幕以相同的增益同时显示纵波和横波时,纵波幅值等于横波的幅值乘以系数γ。
由于存在声速扩散角,在空气和工件上、下表面的交界面都会发生声波模式转换。假设横波转换纵波的效率是α,即入射1单位的横波,转换为α倍纵波和1-α倍横波。同理,假设纵波转换横波的效率为β,当声速扩散角很小时,结合Christoffel方程推导,得
β≈α
(3)
2 试验过程
选择便携式大功率超声检测仪PREMAT-HS200和电磁超声横波换能器,建立试验平台(见图1)。检测工件为JB/T 4730-2005《承压设备无损检测》中规定的CSK-ⅡA标准试样,材料为20钢。几何形状是长方体,标称尺寸分别为长300 mm、宽60 mm和高40 mm。电磁超声换能器放置在300 mm×60 mm的平面上,距离工件左边缘170 mm,上边缘35 mm。常温下,千分尺实测工件高为40.02 mm。系统激发超声横波和纵波的传播路径示意如图2所示,图中,“T”代表横波,“L”代表纵波。

图1 试验平台外观
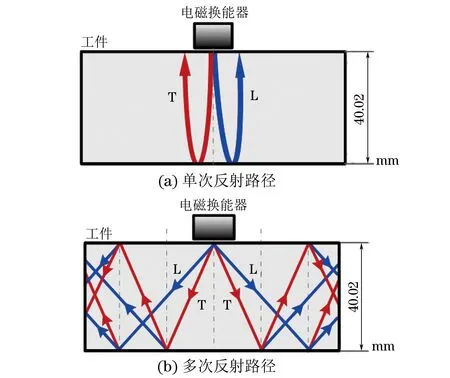
图2 系统激发超声横波和纵波的传播路径示意
设置大功率电磁超声检测仪的发射频率为4 MHz,激励电压为1 200 V,延时为10 μs(目的是不采集始波信号),采样时间为80 μs,增益为自动增益,接收的超声波信号如图3所示。图中有3个非常大的波包,分别为横波第1次回波(T1)、横波第2次回波(T2)和横波第3次回波(T3),且呈指数衰减趋势,这是由于超声波的传播衰减造成的。除此外,信号的信噪比优异,其他反射回波的波包也清晰可见。
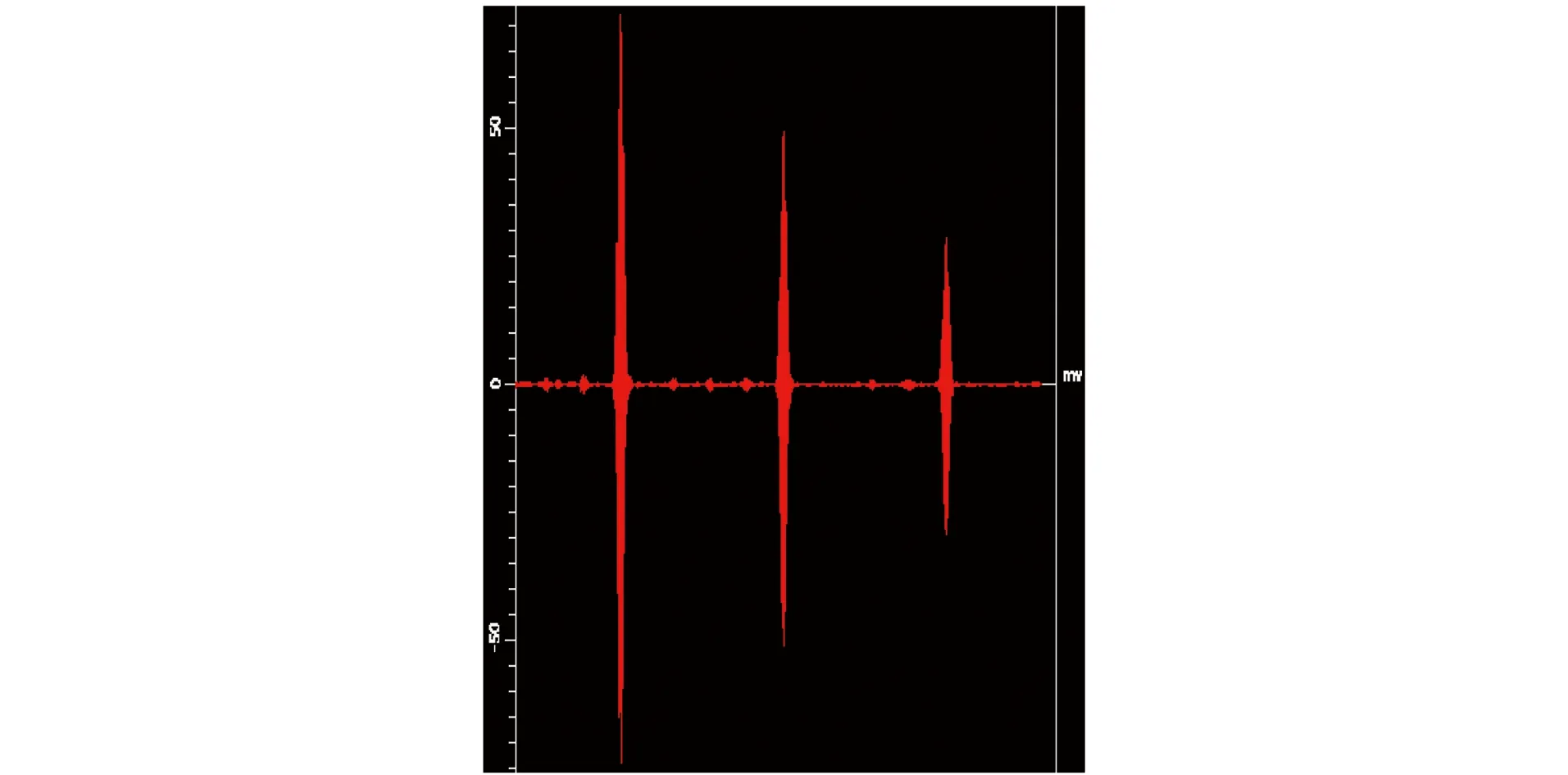
图3 电磁超声检测仪接收的超声波信号
3 试验结果
提取电磁超声检测仪接收的超声波信号,对信号平均并取包络,结果如图4所示。
横波反射回波分别为T1,T2和T3,纵波反射回波分别为L1,L2,L3和L4;模式转换回波为W1~
W8。记超声波的单程传播路径(工件上表面至下表面或者工件下表面至上表面)中横波的传播为“T”,纵波的传播为“L”,波包之间的叠加为“+”,则波包T1、波包T2和波包T3分别标记为TT,TTTT和TTTTTT,分别表示横波的第1次反射回波、第2次反射回波和第3次反射回波;波包L1、波包L2和波包L3分别标记为LL,LLLL和LLLLLL,分别表示纵波的第1次反射回波、第2次反射回波和第3次反射回波;波包W1~波包W8分别标记为TL+LT,TLLL+LTLL,TTLL,TTTL+TTLT+LTTT+TLTT,TLLLLL+LTLLLL,TTLLLL+LLTTLL,TTTTLL和TTTTLT+TTTTTL+TTTLTT+TTLTTT+ LTTTTT+ TLTTTT,表示模式转换产生的反射回波。波包W1表示横波激发模式转换为纵波和纵波激发模式转换为横波的两个波包的叠加,其他同理。
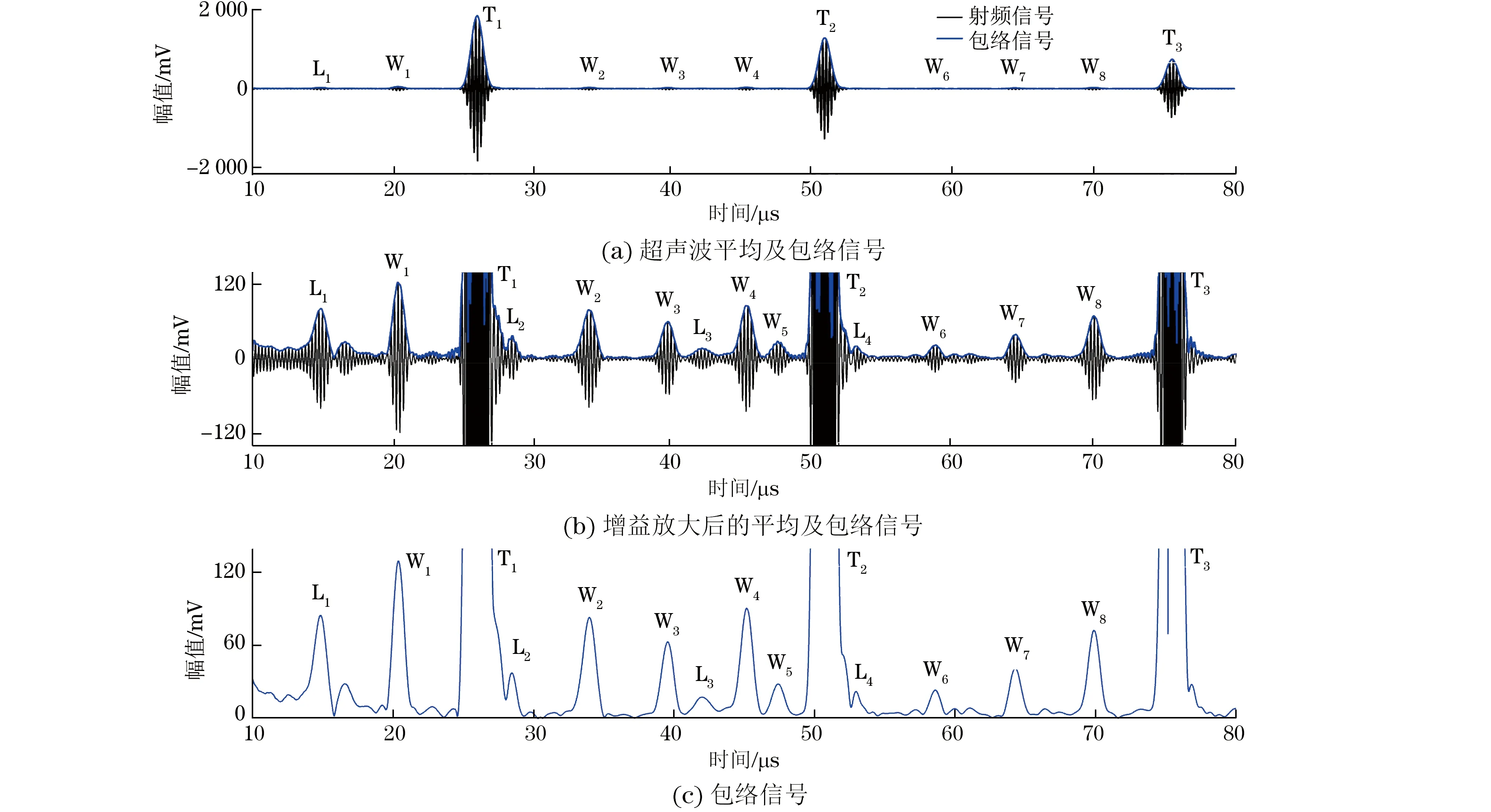
图4 接收超声波信号处理后的结果
对图4(c)的包络信号进行插值,分别取幅值较大的波包(波包T1、波包T2、波包T3、波包L1、波包W1、波包W2、波包W3和波包W4)的最大幅值及其对应时间,数据分别如表1,2所示。其他波包暂不进行分析,故不获取数据。
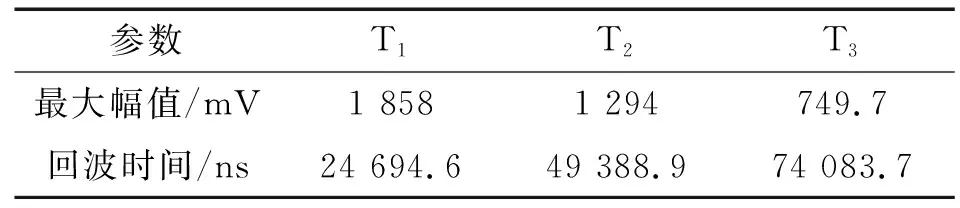
表1 横波反射回波的最大幅值及对应时间

表2 纵波和模式转换回波的最大幅值及对应时间
记横波反射回波的波包T1,T2和T3的最大峰值对应的时间分别为tT1,tT2和tT3,横波的单程传播路径时间为tT,则tT1=Δt+2×tT,tT2=Δt+4×tT,tT3=Δt+6×tT。电磁超声测试系统已被校准,认为系统采样延时Δt≈0。结合表1,分别取tT1,tT2和tT3的回波时间,计算横波的平均传播时间为24 694.53 ns,结合横波的传播距离80.04 mm,计算工件中横波的声速为3 241.20 m·s-1。计算的横波平均传播时间和tT1非常接近,故可看出,系统校准成功。且tT1,tT2和tT3的倍数关系也很明显,故计算出的横波声速比较准确。
同理,记纵波和模式转换回波的波包L1,W1,W2,W3和W4的最大峰值及其对应时间分别为tL1,tW1,tW2,tW3和tW4,纵波的单程传播时间为tL,则tL1=Δt+2×tL,tW1=Δt+tT+tL,tW2=Δt+tT+3×tL,tW3=Δt+2×tT+2×tL,tW4=Δt+3×tT+tL。分别计算波包L1,W1,W2,W3和W4的传播速度分别为5 967.57,5 972.38,5 917.83,5 915.89,5 914.45 m·s-1,将平均值5 937.62 m·s-1记为工件中超声纵波的声速。由于波包能量小,幅值较低,计算的纵波传播声速浮动相对较大。
结合以上计算的超声横波和超声纵波的传播声速,取材料密度为7.86×103kg·m-3,代入式(1)和(2),计算20钢材料的杨氏模量和泊松比分别为
(4)
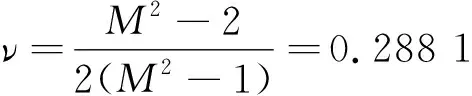
(5)
假设电磁超声换能器激励时工件表面的横波幅值为AT,纵波幅值为AL,工件厚度为d,横波衰减系数为s,纵波衰减系数为l。记图4(c)中波包L1,W1,T1,W3和W4的幅值分别为AL1,AW1,AT1,AW3和AW4,则
AL1=γ2AT(1-α)e-2ld
(6)
AW1=2αγATe-(l+s)d
(7)
AT1=(1-α)ATe-2sd
(8)
AW3≈2α(1-α)2γATe-2(s+l)d
(9)
AW4≈2α(1-α)[γ(1-α)+α]ATe-(3s+l)d
(10)
消去指数衰减项,得
(11)
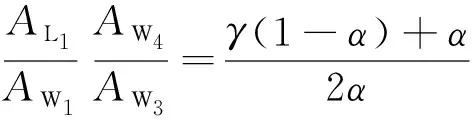
(12)
解得α=9.5%,γ=9.2%。
即横波转为纵波(或者纵波转横波)的模式转换效率为9.5%,系统激发纵波的效率是激发横波效率的9.2%。
4 结语
提出了一种利用电磁超声波检测各向同性金属材料弹性模量的方法。该方法操作简单,测量方便,并且不需要耦合剂,避免了压电超声检测使用耦合剂带来的误差,提高了检测精度。
借助大功率电磁超声检测系统,通过电磁超声换能器对标准工件(材料为20钢)进行了检测,对接收的超声波信号进行了分析。
