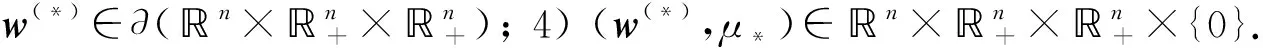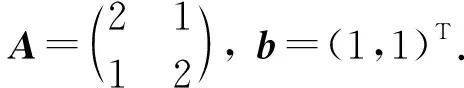基于同伦方法构造绝对值方程解存在的条件
2018-11-28姜兴武姜舶洋杨雪莹王秀玉
姜兴武, 姜舶洋, 杨雪莹, 王秀玉
(1. 吉林工商学院 基础部, 长春 130507; 2. 北京工业大学 信息学部, 北京 100022;3. 北京邮电大学 国际学院, 北京 100876; 4. 长春工业大学 基础科学学院, 长春 130012)
1 引言与预备知识
考虑如下形式的绝对值方程:
Ax-|x|=b,
(1)
其中:A∈n×n;b∈n; |x|表示向量x的每个分量取绝对值. 目前, 关于绝对值方程的研究已有很多结果: 文献[1]获得了绝对值方程与水平线性互补问题的等价关系; 文献[2-4]描述了求解绝对值方程的有效算法; 文献[5-7]研究了绝对值方程解存在的条件. 组合同伦方法是求解优化及互补问题的一个有效方法[8-9]. 本文结合绝对值方程与互补问题的关系, 运用组合同伦方法给出绝对值方程解存在的一个条件, 该条件不同于目前常用的正则性条件. 实例分析表明, 该条件不满足正则性, 但满足本文条件的绝对值方程有解且解不唯一. 用xT表示向量x的转置, (xT,yT,zT)T记为(x,y,z).分别表示向量的分量非负(正)的向量集合. 若也记为x≥0(x>0),I表示单位矩阵.
定义1[2]如果对任意的矩阵B∈[A-I,A+I]均为非奇异的, 则方阵区间[A-I,A+I]称为正则的; 否则该矩阵区间称为奇异的.
引理1[1]绝对值方程(1)等价于如下广义线性互补问题:
y=(A-I)x-b≥0,z=(A+I)x-b≥0,yTz=0.
由引理1知, 求解绝对值方程问题可转化为求解广义线性互补问题.
假设:
(H1) 矩阵A可逆, 且有
[(A-I)x]∘[(A+I)x]≤0⟹[(A-I)x]∘[(A+I)x]=0,
即矩阵对(A-I,A+I)为列充分矩阵对, 其中:I为单位矩阵; ∘表示对应分量乘积.
(H2) 绝对值方程Ax-|x|=0只有零解x=0, 即广义线性互补问题
y=(A-I)x≥0,z=(A+I)x≥0,yTz=0
只有零解.
下面举例说明条件(H1),(H2)与区间矩阵[A-I,A+I]的正则性不同.

若(A-I)x∘(A+I)x≤0, 则有
若x1+x2>0, 由(x1+x2)(3x1+x2)≤0及(x1+x2)(x1+3x2)≤0, 必有3x1+x2≤0和x1+3x2≤0, 这与x1+x2<0矛盾. 若x1+x2<0, 由(x1+x2)(3x1+x2)≤0且(x1+x2)(x1+3x2)≤0, 则有3x1+x2≥0和x1+3x2≥0, 这与x1+x2<0矛盾. 因此x1+x2=0, 即假设(H1)成立.
对于
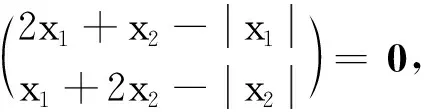
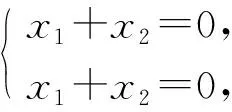
2 主要结果

(2)
其中Y,Y(0)分别为以向量y,y(0)的元素为对角元素的对角矩阵.
其有唯一解x=x(0),y=y(0),z=z(0). 若μ=0, 则式(2)为

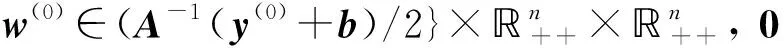
证明: 由于w(0)也可视为变量, 因此H的Jacobi矩阵为
非奇异, 其中μ∈(0,1]. 从而0是H(w,w(0),μ)的正则值, 其余证明与文献[9]中命题2.1相同, 故略.


(A-I)x(k)-b-y(k)+μk(A+I)x(k)=0;
(3)
由同伦方程(2)的第二个式子得
(1-μk)[(A+I)x(k)-b]-z(k)+μkz(0)=0;
(4)
由同伦方程(2)的第三个式子知, 对任意的i=1,2,…,n, 有
(5)
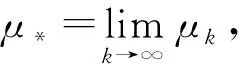
情形1)μ*≠1. 将式(3),(4)两边同乘1/‖x(k)‖, 得
(6)
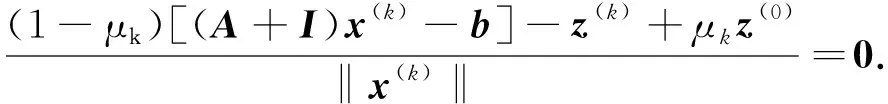
(7)
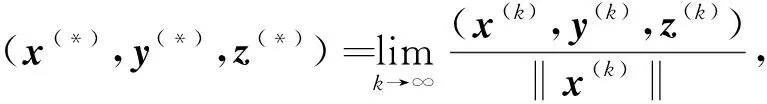
(A-I)x(*)-y(*)+μ*(A+I)x(*)=0,
(8)
(1-μ*)(A+I)x(*)-z(*)=0.
(9)
由式(8),(9)得
(10)

(11)
由式(5)可知, 对任意的i=1,2,…,n, 有
(12)
若μ*=0, 则‖x(*)‖=1, 式(10)~(12)与条件(H2)矛盾, 因此μ*≠0. 由式(12), 对任意的i=1,2,…,n, 有
(13)
结合式(10),(11),(13)及条件(H1), 可得z(*)=0. 但z(*)=0, ‖x(*)‖=1, 式(10),(11),(13)与条件(H2)矛盾.
情形2)μ*=1.
① {(1-μk)x(k)}仍无界, 即‖(1-μk)x(k)‖→∞,k→∞. 将式(3)两边同乘(1-μk), 得
(1-μk)(A-I)x(k)-(1-μk)b-(1-μk)y(k)+μk(1-μk)(A+I)x(k)=0.
(14)
将式(4),(14)两边同乘1/‖(1-μk)x(k)‖, 得
(15)
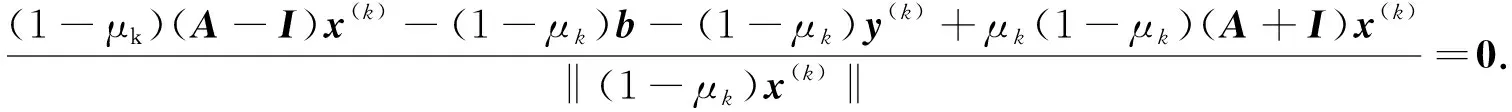
(16)
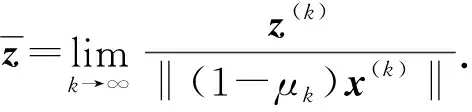
(17)
(A-I)x(*)-y(*)+(A+I)x(*)=0.
(18)
由式(17),(18), 得
(19)
由式(5)得
(20)
由式(20)得
(21)

② {(1-μk)x(k)}有界. 注意到{(1-μk)x(k)}有界, 有界序列必有收敛子列, 其收敛子列仍记为{(1-μk)x(k)}. 令
对式(4),(14)两边取极限, 并注意到μ*=1,
(22)
由式(5)得
(23)
由式(23), 得
(24)

z(k)→z(0).
(25)
由式(5),(25)及μ*=1得
y(k)→y(0).
(26)
由式(3),(26)条件(H1)和μ*=1, 得
x(k)→x(0).
(27)
式(25)~(27)与{(x(k),y(k),z(k))}无界矛盾. 因此,Γw(0)为有界光滑曲线.
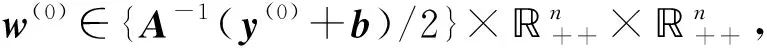
证明: 由定理1和定理2知,Γw(0)为有界光滑曲线. 由一维流形分类定理知,Γw(0)或者微分同胚单位圆周, 或者微分同胚单位区间(0,1]. 而
且
非奇异, 因此Γw(0)只能微分同胚单位区间. 令(w(*),μ*)为Γw(0)的极限点, 则可能出现以下4种情形: