Lyapunov函数在一类随机扰动的SIS-VS传染病系统中的应用

夏 兰, 赵亚男

(1. 吉林大学 计算机科学与技术学院, 长春 130012;2. 吉林交通职业技术学院 基础部, 长春 130012; 3. 长春大学 理学院, 长春 130022)

目前, 关于布朗运动驱动的随机传染病模型的研究已取得许多成果[1-7]. 文献[1]研究了一类具有疫苗接种效应的随机SIS传染病模型:

(1)

其中:Bi(t)(i=1,2,3)表示独立的布朗运动;σi表示其强度；S(t)表示易感人群在t时刻的数量；I(t)表示感染人群在t时刻的数量；V(t)表示接受疫苗接种且免于感染的人群数量； 参数A表示新生儿输入；q表示新生儿接种疫苗的概率；β表示S和I的接触率；μ和γ分别表示自然死亡率和I仓室的恢复率；p表示易感人群中免疫接种的比例系数；ε表示接种人群中丧失免疫力率；α表示感染人群的疾病致死率； 所有参数均为正常数.

在传染病动力学的研究中, 主要考虑疾病何时灭绝或流行. 在确定性模型中, 该问题通过模型的无病平衡点和地方病平衡点的全局吸引或全局渐近稳定性确定, 通常用R0表示传染病系统的基本再生数. 文献[8]研究了系统(1)相应的确定性模型, 表明该模型总存在无病平衡点P0(S0,0,V0). 如果R0≤1, 则P0是唯一的平衡点且全局稳定； 如果R0>1, 则P0不稳定, 且存在一个地方病平衡点P*(S*,I*,V*), 当参数α满足不等式

(μ+ε)(2μ+α)2>α2(μ+ε+p)

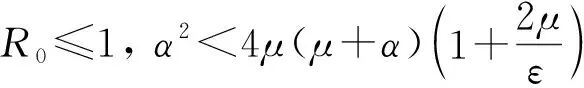
及白噪声扰动小时, 平稳分布存在且是遍历的, 即疾病将流行. 但该结果平稳分布存在性的条件冗长, 而且依赖于相应确定性模型的地方病平衡点P*, 并受参数α的限制, 这主要是由于Hasminskii定理要求满足一致椭圆条件. 因此本文提出一种新的证明方法, 通过寻找一个新的Lyapunov函数, 改进文献[1]的结果, 获得了平稳分布存在性和遍历性的较好条件.

本文令(Ω,F,{Ft}t≥0,P)是一个完备的概率空间, 具有流{Ft}t≥0满足通常条件(即右连续和F0包含所有零测集),B(t)是概率空间上定义的一个标量布朗运动.

设X(t)是El(l维欧氏空间)中的一个自治Markov过程, 可表示为随机微分方程

(2)

引理1[9]设X(t)为El中的正则自治Markov过程, 若X(t)相对于某个有界区域U是常返的, 则其相对于El中的任一非空区域是常返的.

下面考虑具有非退化扩散项随机系统的平稳分布. 假设：

(H1) 存在具有正则边界Γ的有界区域U⊂El, 具有如下性质:

1) 在U及其一些邻域, 扩散阵Λ(x)的最小特征值是非零的；

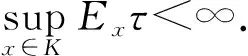
定理1[9]若假设条件(H1)成立, 则Markov过程X(t)存在不变分布μ(·). 令f(·)为关于测度μ可积的函数, 则对所有的x∈El, 成立

引理2[9]设X(t)为El中的正则自治Markov过程, 若X(t)相对于某个有界区域U是常返的, 则其相对于El中的任一非空区域是常返的.

下面给出本文的主要结果.

定理2若

其中k1,k2是正常数, 满足

(3)

函数H(S,I,V)满足

(4)

由式(4), 有

(5)

将式(5)代入式(4), 有

其中θ∈(0,τ),

(6)

其中:

W2=-logS;W3=-logI;W4=-logV.

则

其中

定义一个闭集

其中δ>0充分小, 满足

(9)

式中:

定义

注意到δ满足式(9), 可得

(10)

(11)

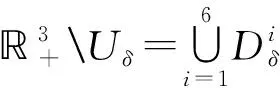
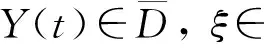
综上, 本文研究了一类具有疫苗接种的随机SIS传染病模型, 通过构造新的Lyapunov函数, 给出了平稳分布存在性和遍历性的充分条件, 改进了文献[1,8]的结果, 去除了因疾病死亡率对平稳分布的影响.