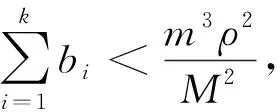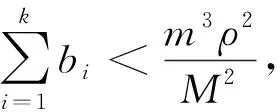高阶多时滞微分方程周期解的存在性
2018-11-28李永祥
章 欢, 李永祥
(西北师范大学 数学与统计学院, 兰州 730070)
0 引 言
时滞微分方程的周期问题在核物理学、 生态学、 流行病学等领域应用广泛[1-6]. 特别是上下解的单调迭代方法已有效应用于低阶时滞微分方程的周期问题. 文献[7]研究了一阶泛函微分方程
u′(t)=f(t,u(t),[p(u)](t)),t∈I=[0,ω]
(1)
的周期边值问题, 运用单调迭代技巧, 得到了方程(1)周期边值问题解的存在性, 其中p:C(I)→C(I). 文献[8]研究了二阶时滞微分方程
-u″(t)=f(t,u(t),u(t-τ1),u(t-τ2),…,u(t-τn)),t∈,
(2)
运用上下解的单调迭代技巧, 得到了方程(2)ω-周期解的存在性. 其中:f∈C(×n+1,), 关于t以ω为周期;τ1,τ2,…,τn为正常数. 但利用上下解的单调迭代方法讨论高阶多时滞微分方程的周期解问题目前文献报道较少.
考虑n阶多时滞微分方程
u(n)(t)+a(t)u(t)=f(t,u(t-τ1),u(t-τ2),…,u(t-τk)),t∈
(3)
ω-周期解的存在性, 其中:n≥2;τ1,τ2,…,τk≥0为常数;a,f满足如下假设:
(H1)a:→(0,∞)连续, 以ω为周期;
(H2)f:×k→连续,f(t,x1,x2,…,xk)关于t以ω为周期.
目前, 对方程(3)中非线性项不含时滞特殊情形的研究已有许多结果[9-11]. 基于此, 本文利用上下解的单调迭代方法考虑更一般的n阶变系数时滞微分方程(3), 得到了该方程ω-周期解的存在性和唯一性.
1 预备知识

[v,w]={u|v≤u≤w}, [v(t),w(t)]={u(t)|v(t)≤u(t)≤w(t),t∈}.
设Mn为正常数, 且
根据文献[10]中引理2.4知, 微分算子Lnu=u(n)+Mu在周期边界条件下满足极大值原理.
引理1[10]设M∈(0,Mn), 则n阶线性边值问题:
存在唯一解Φ∈Cn[0,ω], 且对∀t∈[0,ω],Φ(t)>0.
引理2[11]设M∈(0,Mn), 则对∀h∈Cω(),n阶线性微分方程
u(n)(t)+Mu(t)=h(t),
(4)
存在唯一ω-周期解

(5)
且解算子T:Cω()→Cω()是线性全连续算子, 其中t∈.
定义正常数ρ为

(6)

引理3设M∈(0,Mn), 对∀h∈Cω(), 线性方程(4)的解算子T:Cω()→Cω()具有下列性质:
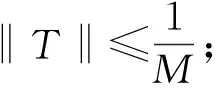

证明: 1) 由式(5)知
故
(7)

证毕.
下面考虑n阶变系数微分方程
u(n)(t)+a(t)u(t)=h(t),t∈
(8)
ω-周期解的存在性.
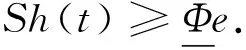
引理4设a满足假设条件(H1), 0 1) 解算子S:Cω()→Cω()为线性有界算子, 其范数 证明: 1) 将方程(8)改写为 u(n)(t)+Mu(t)=(M-a(t))u(t)+h(t),t∈. (9) 设A:Cω()→Cω()是如下定义的线性有界算子: Au(t)=(M-a(t))u(t),u(t)∈Cω(), 显然 ‖A‖≤M-m. 由式(9)易见, 方程(8)的ω-周期解问题等价于Banach空间Cω()中的算子方程 (I-TA)u=Th, (10) 其中T:Cω()→Cω()是由式(5)给出的方程(4)的ω-周期解算子,I是Cω()中的单位算子. 由于 因此I-TA有有界逆算子(I-TA)-1, 且 (11) (12) 故方程(10)等价的方程(8), 有唯一的ω-周期解: (13) 由式(7),(12), 有 故 (14) (15) 另一方面, 由于 所以由T,A的正性, 有 (16) 因为 所以 从而有 将其代入式(16), 有 于是对∀s∈, 有 (17) 因此由式(6),(15),(17), 有 (18) 证毕. 下面考虑带时滞的n阶微分方程 (19) ω-周期解的存在性. 其中bi≥0,i=0,1,2,…,k. 引理5设a满足假设条件(H1), 0 则对∀h∈Cω(), 方程(19)有唯一的ω-周期解u∶=Ph∈Cω(), 且解算子P:Cω()→Cω()是一个正的线性全连续算子. 证明: 设B:Cω()→Cω()是按下式定义的线性算子: 显然,B:Cω()→Cω()是一个正的有界线性算子, 且由方程(8)的ω-周期解的表示式(13)知,u是方程(19)的ω-周期解当且仅当u满足算子方程 (I+SB)u(t)=Sh(t),t∈. (20) 因此I+SB有有界逆算子(I+SB)-1, 且 (21) (22) 故算子方程(20)有唯一解 (23) 其为方程(19)的ω-周期解. 由式(13)知,S:Cω()→Cω()是线性全连续算子, 又由(I+SB)-1的有界性知,P=(I+SB)-1S是全连续的. 由式(14),(22),(23), 有 由算子S和B的定义及SB的性质, 可得 从而 因此(I-SB)S是正的. 即P:Cω()→Cω()是一个正算子. 证毕. 则u(t)≥0,t∈. 证明: 令 定义1设v0∈Cωn(), 若v0满足 v0(n)(t)+a(t)v0(t)≤f(t,v0(t-τ1),v0(t-τ2),…,v0(t-τk)),t∈, 则称v0是方程(3)的一个下ω-周期解, 若不等号取反向, 则称其为方程(3)的一个上ω-周期解. 假设: 定理1假设条件(H1),(H2)成立, 且0 证明: 记 D=[v0,w0]={u∈Cω()|v0≤u≤w0}. 定义算子F:D→Cω()为 ∀u∈D, 则F:D→Cω()连续、 有界, 且是增算子. 根据引理5, 方程(3)在D中的解等价于算子 Q=P∘F:D→Cω() 的不动点. 由F的序增性及P的正性可知,Q=P∘F是增算子, 即对∀u1,u2∈[v0,w0], 满足u1≤u2, 则有Qu1≤Qu2. 下面对Q应用增算子不动点定理单调迭代求解, 分3步证明. 1) 证明v0≤Qv0,Qw0≤w0. 令v1=Qv0,v=v0-v1, 则由条件(H3)及下ω-周期解的定义, 有 根据引理6知, ∀t∈,v(t)≤0, 即v0≤Qv0. 类似地, 可证Qw0≤w0. 2) 证明算子Q在D中有不动点. 分别以v0和w0为初始元作迭代序列, vn=Qvn-1,wn=Qwn-1,n=1,2,… (24) 根据算子Q的单调性, 有 v0≤v1≤v2≤…≤vn≤…≤wn≤…≤w2≤w1≤w0, 则{vn}和{wn}分别在序区间D上单调递增和单调递减. 由Q的紧性知, {vn},{wn}⊂[v0,w0]为Cω()中的相对紧集, 有一致收敛的子列. 因此{vn}和{wn}均在Cω()中收敛, 即∃u*,u*∈Cω(), 使得vn→u*,wn→u*. 又因为D为Cω()中的凸闭集, 故u*,u*∈D. 在式(24)中令n→∞, 则由Q的连续性知,u*=Qu*,u*=Qu*. 因此u*和u*均为算子Q在D中的不动点. 3) 证明u*和u*分别为算子Q的最小不动点和最大不动点. (25) 假设: (H4) 存在常数b1,b2,…,bk≥0及c1,c2,…,ck≥0, 满足 且对∀(t,x1,x2,…,xk),(t,y1,y2,…,yk)∈×k, 当v0(t-τi)≤xi≤yi≤w0(t-τi)(i=1,2,…,k)时, 有 证明: 由定理1可知, 当假设条件(H3)成立时, 方程(3)在v0与w0之间存在最小ω-周期解u*和最大ω-周期解u*. 下面只需证u*=u*即可. 令r=u*-u*, 由假设条件(H4)知, 对∀t∈, 有 则 结合引理6可知r(t)≥0(t∈), 则u*≥u*. 又由定理1的证明过程可知u*≤u*, 故 假设: 定理3假设条件(H1),(H2)成立, 且0 (26)
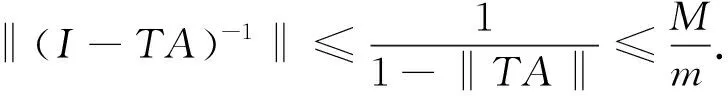



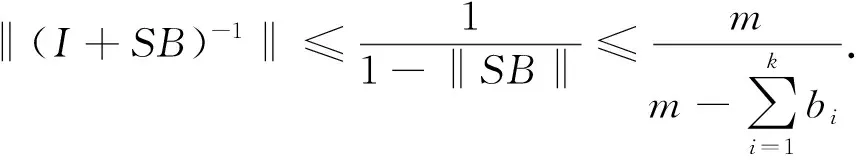




2 主要结果