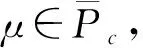一类具有p-Laplace算子的非线性分数阶微分方程解的存在性与多解性
2018-11-28李继梅李辉来
李继梅, 李辉来
(吉林大学 数学学院, 长春 130012)
1 引言与预备知识
分数阶微分方程在经济学、 物理、 化学和工程等领域应用广泛[1-4]. 目前, 利用一些不动点定理(如Schauder不动点定理、 Guo-Krasnosel’skii不动点定理、 Leggett-Williams不动点定理)和上下解的方法, 研究非线性分数阶微分方程边值问题正解的存在性与多解性已有很多结果[5-12].
本文考虑如下非线性分数阶微分方程:
(1)

定义1[3]连续函数y: (0,+∞)→的α>0阶Riemann-Liouville分数阶积分定义为
其中等式右端在(0,+∞)内有定义.
定义2[3]连续函数y: (0,+∞)→的α>0阶Caputo分数阶导数定义为
其中n是大于或等于α的最小整数.
引理1[3]设α>0, 假设μ∈Cn[0,1], 则
其中n是大于或等于α的最小整数.
引理2[11]设y∈C[0,1], 2<α≤3, 则分数阶微分方程边值问题:
有唯一解

其中
(2)
引理3设y∈C[0,1], 2<α≤3, 1<β≤2, 则分数阶微分方程边值问题:
有唯一解
(5)
其中:G(t,s)由式(2)定义;
(6)
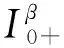
则
由边值条件(4), 得
因此,
从而
于是, 分数阶微分方程边值问题(3)-(4)等价于下列问题:
由引理2可知, 分数阶微分方程边值问题(3)-(4)有唯一解式(5). 证毕.
引理4由式(2),(6)所定义的函数G(t,s),H(t,s)满足如下性质:
1) 对任意的t,s∈[0,1],G(t,s)≥0,H(t,s)≥0;
2) 对任意的t,s∈[0,1],G(t,s)≤G(1,s),H(t,s)≤H(s,s);
3) 对任意的t,s∈(0,1),G(t,s)≥tα-1G(1,s);
4) 存在两个正函数δ1,δ2∈C[0,1], 满足
证明: 由文献[11]中引理2.10可知G(t,s)满足性质1)~3).
下面证明函数G(t,s)的性质4)和函数H(t,s)的性质. 由简单计算可知, 函数G(t,s)当s≤t时关于t是递增的, 当t≤s时关于t也是递增的. 于是, 令
则有
其中:
由函数G(t,s)的单调性, 有
于是, 设
则式(7)成立.
由H(t,s)的表达式可知, 对任意的t,s∈[0,1],H(t,s)≥0成立. 当s≤t时,H(t,s)关于t是递减的, 因此

从而式(8)成立. 证毕.
定义3[5]若θ:P→[0,∞)是连续的, 且对任意的x,y∈P, 0 1) ‖Ax‖≤‖x‖,x∈P∩∂Ω1, 且‖Ax‖≥‖x‖,x∈P∩∂Ω2; 2) ‖Ax‖≥‖x‖,x∈P∩∂Ω1, 且‖Ax‖≤‖x‖,x∈P∩∂Ω2. P(θ,b,d)={x∈P|b≤θ(x), ‖x‖≤d}. 1) 当x∈P(θ,b,d)时, 集合{x∈P(θ,b,d)|θ(x)>b}非空且θ(Ax)>b; 2) 当‖x‖≤a时, ‖Ax‖ 3) 当x∈P(θ,b,c)且‖Ax‖>d时, 有θ(Ax)>b. 则A至少有3个不动点x1,x2,x3, 满足: ‖x1‖ 注1[5]如果d=c, 则由引理6中条件1)可推出条件3), 即只需证明条件1),2)即可得到算子A至少有3个不动点x1,x2,x3. 引理7A:P→P是全连续算子. 证明: 首先, 对μ∈P, 由函数G(t,s),H(t,s)和f(t,μ(t))的连续性和非负性, 可知A:P→P是连续的. 因此A(Ω)是一致有界的. 另一方面, 由于G(t,s)在[0,1]×[0,1]上是一致连续的, 因此对固定的s∈[0,1]及任意的ε>0, 存在δ>0, 使得当t1,t2∈[0,1], |t2-t1|<δ时, 有 于是 即A(Ω)是等度连续的. 由Arzel-Ascoli定理可知,A:P→P是全连续的. 证毕. 记 定理1假设f(t,μ)为C[0,1]×[0,∞)上的连续函数, 且存在两个不同的正常数r1,r2, 满足下列假设条件: 1) 当(t,μ)∈[0,1]×[0,r1]时,f(t,μ)≤φp(Mr1); 2) 当(t,μ)∈[1/4,3/4]×[0,r2]时,f(t,μ)≥φp(Nr2). 则边值问题(1)至少有一个正解μ, 使得min{r1,r2}≤‖μ‖≤max{r1,r2}. 证明: 由引理7可知A:P→P是全连续算子. 不失一般性, 不妨设0 首先, 令Ω1∶={μ∈P|‖μ‖ 因而‖Aμ‖≤‖μ‖,μ∈∂Ω1. 其次, 令Ω2∶={μ∈P|‖μ‖ 因而‖Aμ‖≥‖μ‖,μ∈∂Ω2. 由引理5可知, 算子A至少有一个不动点μ, 即边值问题(1)至少有一个正解且满足r1<‖μ‖ 定理2假设f(t,μ)为C[0,1]×[0,∞)上的连续函数, 若存在正常数0 1) 当(t,μ)∈[0,1]×[0,a]时,f(t,μ)≤φp(Ma); 2) 当(t,μ)∈[1/4,3/4]×[b,c]时,f(t,μ)≥φp(Nb); 3) 当(t,μ)∈[0,1]×[0,c]时,f(t,μ)≤φp(Mc). 则边值问题(1)至少有3个正解μ1,μ2,μ3, 满足 (9) 证明: 由于A:P→P全连续, 因此边值问题(1)有解μ=μ(t)当且仅当μ满足算子方程μ=Aμ(t). 即只需证明引理6的所有条件均满足即可. 因而{μ∈P(θ,b,c)|θ(μ)>b}≠Ø. 若μ∈P(θ,b,c), 则有b≤μ(t)≤c. 从而当t∈[1/4,3/4]时, 由假设条件2), 有 即对μ∈p(θ,b,c),θ(Aμ)>b. 表明引理6中的条件1)成立. 由引理6和注1可知, 边值问题(1)至少有3个正解μ1,μ2,μ3满足式(9). 证毕.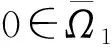

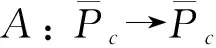
2 存在性和多解性