一种新型机械式无级变速器传动方案设计及仿真
2018-11-28牛善田李红勋汪正西
牛善田 李红勋 汪正西
陆军军事交通学院 天津 300161
1 前言
机械式无极变速器具有结构简单、维护方便、传动平稳等优点[1],但当前的传动形式多为摩擦传动,相比通过齿轮传动的手动变速器,存在传动扭矩小,传动效率低等缺点,仅适用于中小型车辆[2]。然而,专用汽车和特种车辆多为重型车辆,其变速器需具备大扭矩的特点,因此为改善其换挡性能,迫切需要开发一种能够满足大扭矩传递的无级变速器。非圆齿轮传动是一种特殊的齿轮传动,其既具有高效传动的优点,又具备变速比传动的特点[3],因此,利用非圆齿轮实现大扭矩、高效率的无级变速传动,无疑是一种值得探究的传动方式。
本文将提出一种通过非圆齿轮传动的新型机械式无级变速器传动方案,并对其进行理论分析和仿真研究,检验其实现无级变速的可行性。
2 传动方案的结构组成
该机械式无级变速器传动方案由相位调节器和3组非圆齿轮无级变速机构组成。相位调节器用以改变两非圆齿轮对的相对位置,实现变速比传动;3组非圆齿轮无级变速机构共用一组输入、输出传动部分,各分支传动部分围绕输入传动部分相间120°周向布置,协调接力实现360°功率流的连续变换。包含相位调节器和单组非圆齿轮无级变速机构的传动简图如图1所示;输入轴主动非圆齿轮和3个分支轴从动非圆齿轮的布置关系如图2所示。
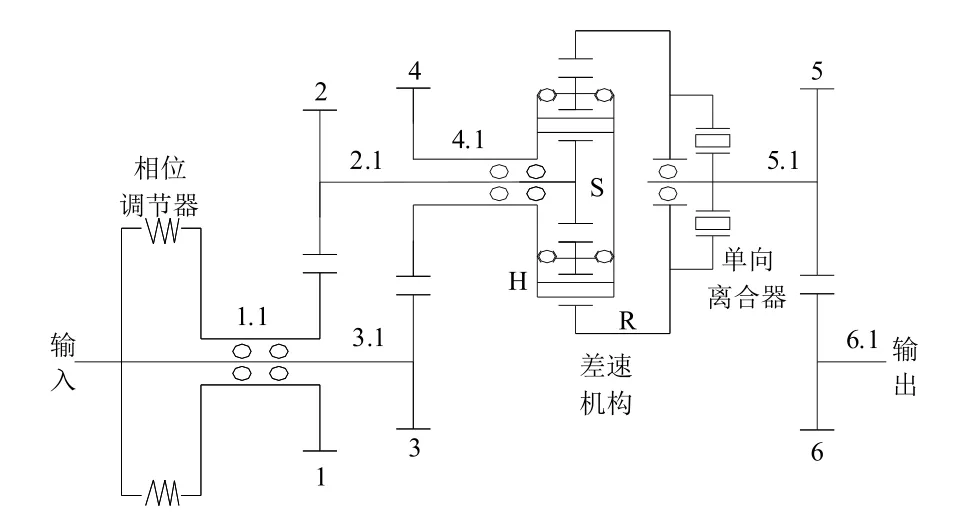
图1 相位调节器和单组非圆齿轮无级变速机构传动简图

图2 主动非圆齿轮和从动非圆齿轮布置关系
相位调节器为双叶摆动液压缸结构,由“转子”和“定子”组成,两者分别与两非圆齿轮对的主动轮1和3固联,且理论上可相对转动240°,调节范围为-120°~+120°。相位调节器的结构简图如图3所示。

图3 相位调节器的结构简图
如图1所示,各组非圆齿轮无级变速机构包括两非圆齿轮对、圆柱齿轮对、差速机构、单向离合器以及若干传动轴,其中差速机构为双内啮合行星齿轮机构。两输入轴1.1和3.1分别与两非圆齿轮对1/2和3/4的主动轮1和3固联,两非圆从动轮2和4通过传动轴2.1和4.1分别与差速机构的太阳轮和行星架相连,齿圈R通过轴5.1和圆柱主动齿轮固连,圆柱从动齿轮通过轴6.1输出动力。该传动方案的动力传递路线如图4所示。
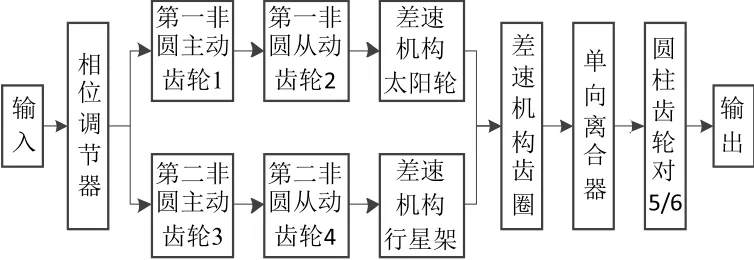
图4 传动方案动力传递路线
该非圆齿轮无级变速器的无级变速思想可概括为动力经具有特定传动比函数的两非圆齿轮对,从两路输入至差速机构,然后在差速机构的叠加作用下,在一定角度内以恒转速输出。通过相位调节装置改变两非圆齿轮对的相对位置,可实现输出速度的连续变化,并由多组这样的变速机构组合在一起,在单向离合器的控制下,各组依次接力工作,实现360°的恒转速输出。
3 速比关系的理论分析
设输入转速为nin,输出转速为nout,第一非圆齿轮对1/2的主、从动轮齿数分别为z1、 z2,第二非圆齿轮对3/4的主、从动轮齿数分别为z3、 z4,圆柱齿轮对5/6的主、从动轮齿数分别为z5、 z6,差速机构齿圈、行星架、太阳轮的转速分别为nR、 nH、 nS, 则n1= n3= nin, nS= z1nin/ z2, nH= z3nin/ z4,nR= z6nout/ z5。
由差速机构特性方程nS+ ( k-1)nH- k nR=0,可得:
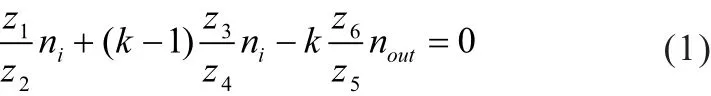
进而可得传动比i为:

令ω1= z1/ z2、 ω3= z3/ z4, 即ω1和 ω3分别为两非圆齿轮对的传动比倒数。非圆齿轮对传动比为变量,而无级变速器却需要输出恒定传动比,鉴于此,文献[4]提出两非圆齿轮对传动比倒数采用线性函数,可在差速机构的叠加作用下输出恒定速比。
为实现恒定传动比输出,令ω1和 ω3在0°~240°工作范围内取线性函数,同时为避免非圆齿轮节曲线存在尖点,在剩余范围内,取余弦函数。两非圆齿轮对在初始位置时,一般参数下的ω1和 ω3以及变速器传动比倒数曲线如图5所示,图中i0为此时变速器的输出传动比。
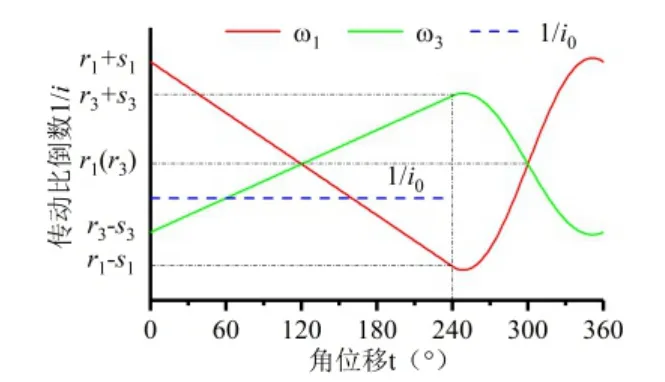
图5 一般参数下的传动比倒数曲线图
不难写出ω1和 ω3在0°~240°线性段范围内的方程为:
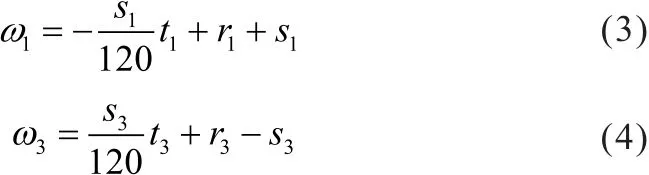
为使非圆齿轮对主从动齿轮的大小差异不至于过大,通常取r1= r3=1,且初始位置下,两非圆齿轮对的相位差为0°,即t1= t3。由于此时在0°~240°线性段范围内有恒定的总传动比i0,特殊地,取t1、 t3为0°、120°、240°时,根据式(2)可得:

即:

因此,将式(3)、(4)和(6)带入式(2)中,可得该传动方案的传动比为:
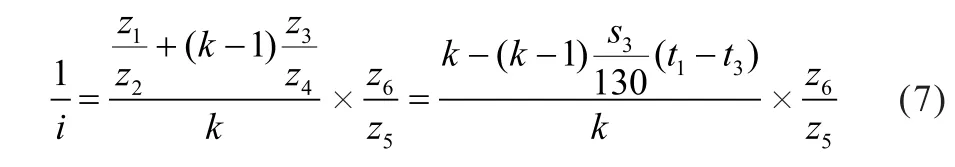
可见,传动i和两非圆齿轮对的相位差(t1- t3)有关,通过调节两非圆齿轮对的相位差即可实现传动比的连续变化,完成无级变速。
相位调节装置为双叶摆动液压缸,其转子和定子可相对转动,调节两非圆齿轮对的相对位置,调节范围为-120°~120°,即ω1相对ω3的移动范围为-120°~120°。设其左移相位差为正、右移相位差为负,相比图5的初始位置,在一般参数下ω1相对ω3左移和右移120°时传动比倒数的曲线分别如图6和7所示。
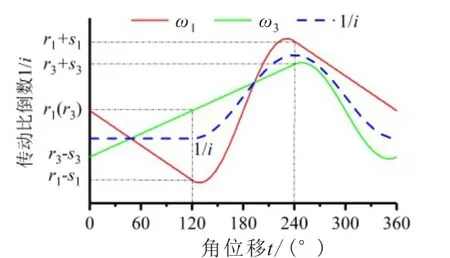
图6 ω1相对ω3左移120°
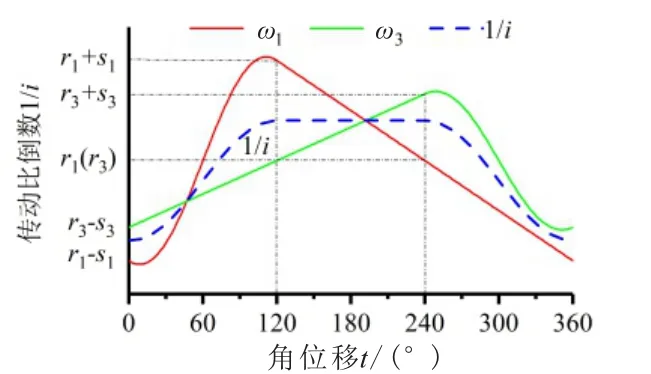
图7 ω1相对ω3右移120°
根据单向离合器的工作特性,当输入转速大于输出转速时,其处于结合状态,反之则处于分离状态。由图3、4的传动比倒数曲线可知,当ω1相对ω3左移,即相位差在[0°,120°]范围内无级变速时,机构转速特性不符合单向离合器的功率流传递特性;当ω1相对ω3右移,即相位差在[-120°,0°]范围内无级变速时,机构转速特性符合单向离合器的功率流传递特性,单向离合器可实现3组非圆齿轮无级变速机构的功率流的连续切换,因此相位差在[-120°,0°]范围内为可用传动比。
故将-120≤t1– t3≤0带入式(7)中可得该非圆齿轮无级变速器的有效传动比范围:
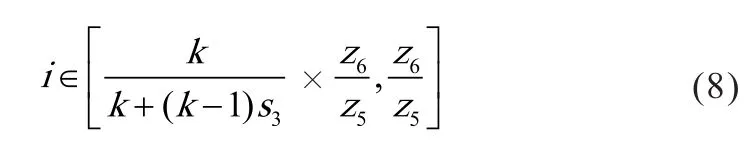
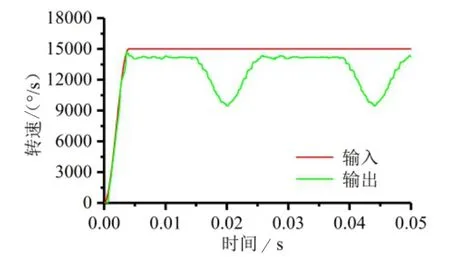
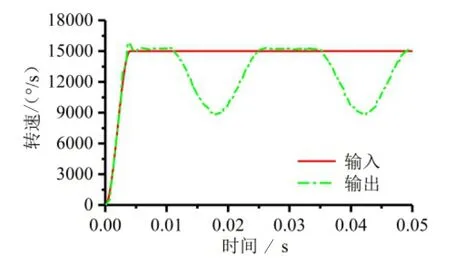
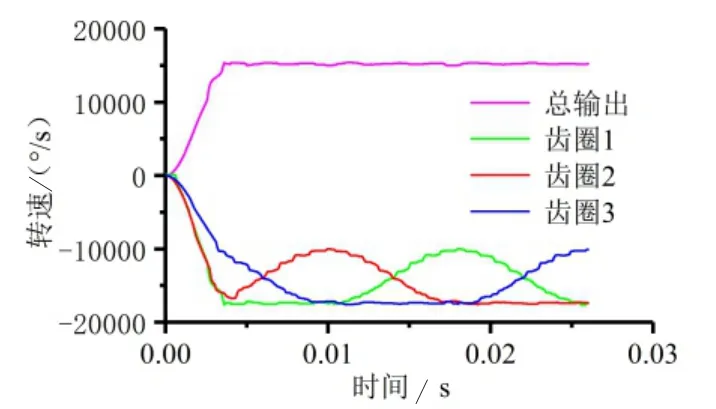
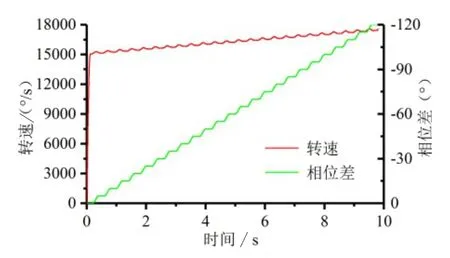
可见,该无级变速器的传动比范围和设计参数的取值密切相关,故可根据传动需求和加工要求确定合适的设计参数,其中差速机构特征值k的取值范围为1 4.1.1 建模于虚拟装配 为便于构建该非圆齿轮无级变速器的虚拟样机模型,取设计参数k=2,r1= r3= 1,s1= s3= 0.32,z6/ z5=32/28,并在SolidWorks中对主要零部件进行三维建模和虚拟装配。由于传动方案中单向离合器和各部件间的相关键连接以及轴承连接可用ADAMS软件的相关命令语句和连接副代替,故在建模过程中对模型进行了一定简化,其装配体的三维图如图8所示,其装配体的剖面视图如图9所示。 图8 三维装配模型 图9 装配体剖面视图 4.1.2 模型导入及定义材料属性 将SolidWorks的转配体模型另存为Parasolid(x.t)格式,导入至ADAMS中,并在ADAMS中添加相关的材料属性。 4.1.3 添加约束及驱动 为正确模拟机构的运动状况,需根据各零部件间的运动关系,建立相关的约束关系。对于该模型需要添加固定副、旋转副和接触约束。其中,固定副用以连接模型中通过键连接或无相对运动的构件,旋转副用以限制零件相对机架的旋转运动,接触约束用以模拟齿轮轮齿间的啮合传动。 根据非圆齿轮无级变速器的工作原理,对于该虚拟样机模型,共涉及两处驱动,一是在输入轴的旋转副上添加旋转驱动,用以模型输入轴的输入转速,即输入驱动;二是在相位调节装置转子和定子间的旋转副上添加旋转驱动,用以实现转子和定子的相对运动,改变两非圆齿轮对的相位差,即相位调节驱动。 为全面探究该非圆齿轮无级变速器的转速特性,先将其中两组非圆齿轮无级变速机构的传动部分压缩隐藏,仅对包含单组非圆齿轮无级变速机构的样机模型进行转速特性分析,为下一步整体模型的仿真分析提供仿真基础。 在输入驱动上添加输入转速2 500 r/min,并通过函数Step(time,0,0,0.004,15000) ,使输入转速在0.004 s内递增至15 000 °/s,以减小突然加速的冲击。另外,分别设置相位调节驱动为0°、-60°、-120°,仿真时间为0.05 s,仿真步数2 000步,得到不同相位差下主动齿轮旋转2个周期的输出轴角速度曲线,分别如图10~13所示。 图10 0°相位差转速仿真 图11 -60°相位差转速仿真 图12 -120°相位差转速仿真 由上述单组非圆齿轮无级变速机构的转速仿真可知,不同相位差下,输出速度不同,若连续改变相位差即可实现无级变速,并且单组非圆齿轮无级变速机构的有效工作区间,即恒速比输出区间亦随相位差的变化而改变,当处于极限相位差-120°时,有效工作区间仅120°,故需要3组非圆齿轮无级变速机构来协调接力实现360°范围内的恒速比输出。 4.3.1 360°范围恒速比输出仿真 由以上分析可知,单组机构的恒速比输出区间随相位差的增加而减少,且当在极限相位差-120°时,其有效工作区间最短,需3组非圆齿轮无级变速机构在单向离合器的作用下协调接力实现360°范围内的恒速比输出。理论上,3组机构的恒转速区间应彼此连续,且根据单向离合器的工作特性,恒定转速的大小应为其整体转速范围的极大值,该变速器才可在单向离合器的作用下实现360°范围内的恒速比输出。 为模拟单向离合器的工作特性,在3组非圆齿轮无级变速机构中,分别添加角速度传感器,用以感知各差速机构齿圈和圆柱主动齿轮的转速。传感器的触发条件设置为齿圈转速大于圆柱主动齿轮转速,并通过创建ADAMS/Solve命令仿真脚本来控制仿真运行,即当某一传感器触发时,该组齿圈和输出轴之间的固定副被激活,当该传感器未触发时,此固定副失效。通过函数Step(time,0,0,0.004,15 000) 设置输入转速在0.004 s内递增至15 000 °/s,并设置相位调节驱动为-120°,得到该相位差下各非圆齿轮无级变速机构的齿圈转速和变速器整体的输出转速曲线如图13所示。 图13 -120°相位差转速仿真 由图13可见,通过设置角速度传感器来模拟单向离合器的工作特性,可实现该变速器在360°范围内的恒转速输出,从而,验证了该变速器通过单向离合器控制3组非圆齿轮无级变速机构协调接力实现360°范围内的恒速比输出的可行性。 4.3.2 相位差连续变换下的输出转速仿真 输出转速随相位差的改变而不断变化,若连续调节非圆齿轮对相位差便可实现该变速器的无级变速,为仿真探究该过程,在ADAMS 中通过函数Step(time,0,0,0.004,15 000)设置输入速度在0.004 s内递增至15 000 °/s,在相位调节驱动添加函数Step,使其每间隔0.2 s调节-5°相位差,且相位调节时间为0.2 s,最后设置仿真时间为9.8 s,仿真步数为5 000步,得到整体机构的输出转速和相位差随时间的变化曲线如图14所示。 图14 相位差连续变换下的输出转速曲线 可见,在不断调节相位差大小的过程中,该虚拟样机的输出转速也随之不断增加,虽然有较小的波动,但其趋势是连续变化的,实现了该虚拟样机无级变速的目的,同时也验证了该非圆齿轮无级变速器传动方案的可行性。 本文提出了一种通过非圆齿轮传动的新型机械式无级变速器传动方案,并基于该传动方案的结构组成,首先理论分析了其传动比范围,其次通过SolidWorks软件建立了其装配模型,最后利用Adams软件对其传动性能进行了仿真研究,验证了其实现无级变速的可行性。另外,本文所述的新型机械式无级变速器传动方案通过非圆齿轮和差速机构组合实现无级变速,其在传动方式上与手动变速器(MT)相同,均是依靠齿轮啮合来传递动力,因此,其传递扭矩和传动效率势必高于依靠摩擦传动的无级变速器,有望满足某些重型专用汽车的传动需求。同时本文内容也为对该类变速器的研究和应用提供了方法和思路,具有一定的参考和指导价值。4 动力学仿真分析
4.1 虚拟样机模型构建
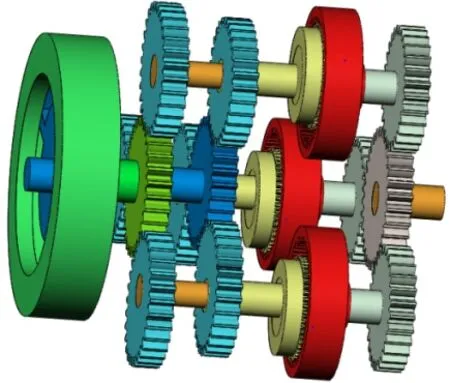
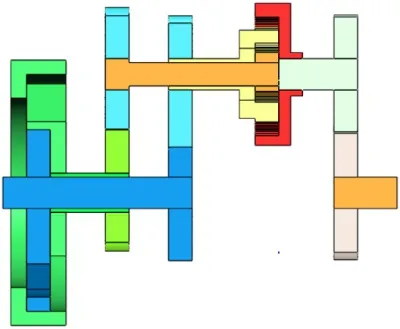
4.2 单组非圆齿轮无级变速机构仿真分析
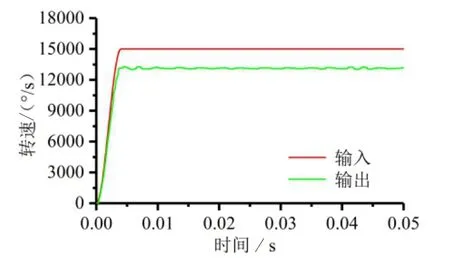
4.3 非圆齿轮无级变速器整体样机仿真分析
5 结语
