AGV轨迹规划及其纠偏控制机理研究*
2018-11-27杨前明
杨前明,张 君,阮 益
(山东科技大学 机械电子工程学院,山东 青岛 266590)
0 引 言
无人数字工厂是棉纺车间未来的发展方向[1]。由于棉纺车间存在高温度、高湿度、高噪音特点,机器人换人势在必行。因此,为纺织车间设计的背负式棉桶更换复合机器人应运而生。
磁导航式差速AGV在前进、转向过程中,路面平整度问题会对AGV行驶产生一定定位精度影响;导航磁带直线度误差以及AGV由直道转入弯道或者由弯道转入直道等情况,也会致使AGV在行驶过程中产生偏差。
国内外关于纠偏控制的研究较多,像多窗口实时测距[2]、串级轨迹跟踪算法、卡尔曼滤波器定位等[3],这些算法以及控制方法比较适合于无轨导航,工程上经常采用PID算法对AGV行驶轨迹进行实时的纠偏[4-5],PID控制器、模糊控制器以及模糊PID比较适合于有轨导航。
在磁导引中,在实现AGV的导引前提下,也不断研究AGV的定位以及纠偏方法,提高AGV的定位精度。PWM调速是利用功率开关的器件的导通与关断,将直流电压变成连续的直流脉冲序列,并通过控制脉冲宽度或周期达到变压调速的目的。
本文以PLC为控制器,基于PWM调速与PID控制,探讨直流电机调速与AGV纠偏调速控制系统的实现方法。
1 AGV纠偏模型建立
1.1 AGV运动学模型建立
自主式磁导航AGV在行驶过程中,随着纠偏传感器位置信号连续采集送入控制器,同时给定直流电机纠偏信号不断接近目标轨迹。
本研究以固定点O为参考点,建立固定参考坐标系I[X-O-Y];以AGV上质心点P作为AGV局部参考系位置参考点,建立局部参考系Ⅱ[XR-P-YR][6],如图1所示。
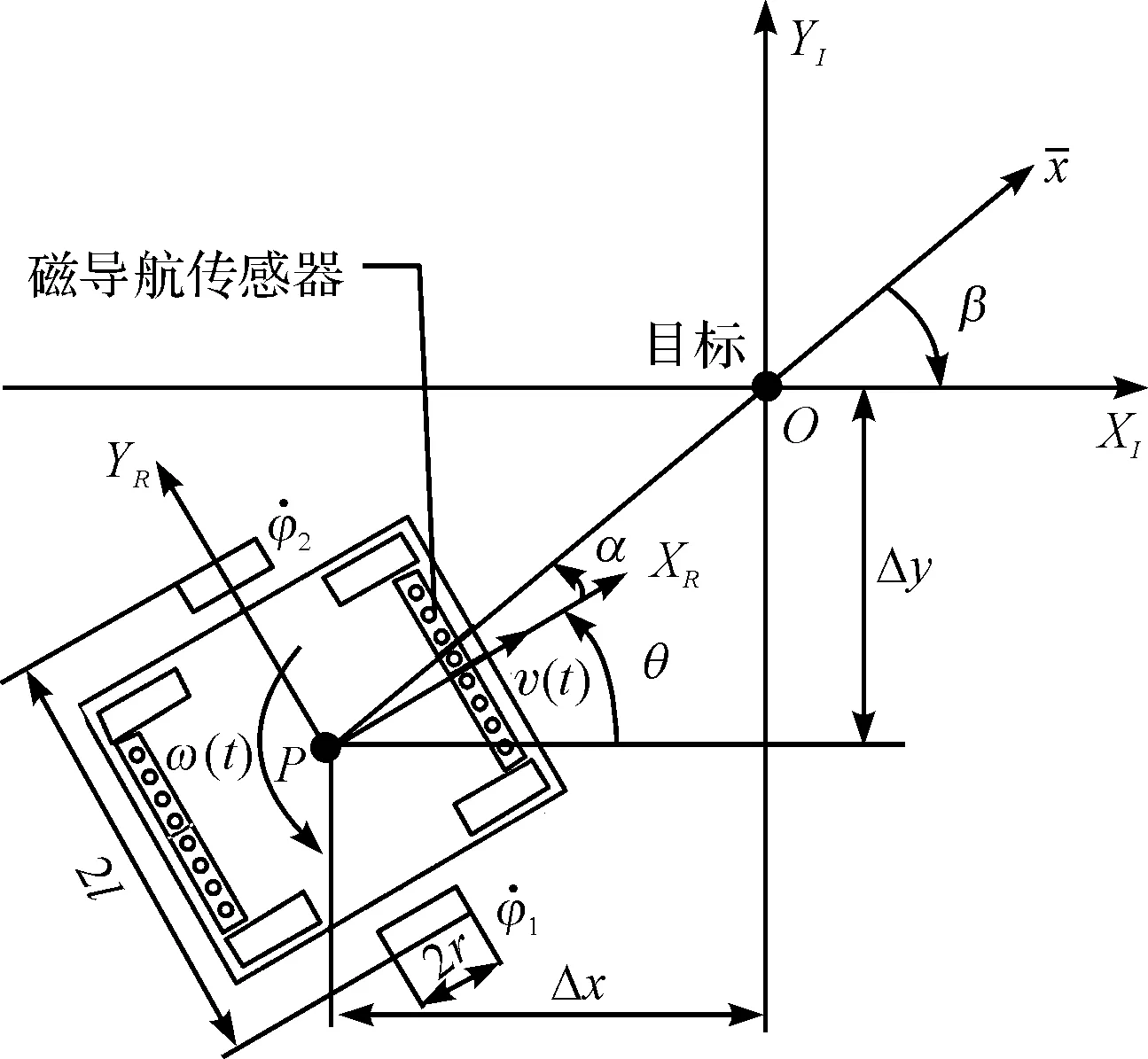
图1 AGV纠偏环节运动模型
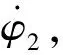
(1)
AGV车体的角速度和线速度为:
(2)
式中:r—车轮半径,mm;l—质心P点至两轮距离,mm;VR—右轮运动速度,mm/s;VL—左轮运动速度,mm/s。
差速驱动AGV的运动学模型为:
(3)
1.2 纠偏调速系统数学模型建立
在图1所示的参考系中,在参考系P{XR,YR,θ}中,AGV上点P(x,y,θ)是其实时位置坐标,参考系I中点O为其目标位置,OP之间距离偏差为(Δx,Δy),为Ⅱ平面XR轴与目标位置向量之间的夹角,即偏差角。
在坐标系I中,AGV运动模型可表述为:

(4)
其极坐标可描述为:
(5)
α=-θ+arctan2(Δy,Δx)
(6)
β=-θ-α
(7)
在新的极坐标中,得到一个系统描述为:
(8)

从式(8)中可以看出,当ρ=0时出现不连续性,但Brockett定理不妨碍平滑稳定性[7],即:
v=kρρ
(9)
ω=kαα+kββ
(10)
由式(8)可得到闭环控制系统的数学模型为:
(11)
式中:ρ—AGV轮轴的中心与目标位置之间的距离,mm;kρ—偏差距离控制参数;kα—偏差角度α控制参数;kβ—β角控制参数。
1.3 纠偏原理
由上述数学模型分析可知:AGV的位置纠偏一直贯穿于其行驶过程,轨迹跟踪就是减少AGV行驶过程中实际轨迹与预定轨迹间的距离偏差ρ与角度偏差α[8]。
当ρ=0时,即(ρ,α,β)=(0,0,0)是一个唯一的平衡点,直流电机驱动AGV行驶至该位置,这就是目标位置。
AGV通过接收磁导航传感器的位置信息,判断此时与预定轨道的位置。若AGV发生偏转,与预定轨道的距离偏差为ρ,角度偏差α,控制器通过PID指令向驱动电机发送调节指令,对AGV轨迹纠偏回归到预定轨道。此时磁导航传感器将位置信号传递给PLC,PLC根据磁导航输出的信号进行处理,从而发出相应的控制指令调节直流电机转速[9]。
2 直流电机纠偏控制系统
2.1 直流电机调速控制系统
本研究采用PWM的调速方式实现对电机转速以及电流的控制。在直流无刷电机控制系统中,采用电流内环、PID外环的闭环控制[10],直流电机动态PWM调速模型如图2所示。

图2 直流电机动态PWM调速模型
无刷直流电机调速系统常常会受到一定外界干扰,虽然直流电机在一定程度上可以对随机干扰进行调节,但是当系统输入值受到外界干扰产生变化时,同时也会引起输出值的变化。若这些偏差不能及时处理,就会产生一定误差。采用PID控制进行补偿,减少干扰对转速的影响是通常采用的方法之一[11]。
2.2 PID纠偏实现方法
将AGV运动过程以左、右轮转速偏差Δv的方式体现,用e表示,输出u为两驱动电机控制电压,则传统的位置式PID纠偏控制表达式可以表示为:
(12)
式中:e(k),ec—系统偏差和系统偏差变化率;KP,KI,KD—比例系数、积分系数和微分系数。
由上式可知,位置式PID算法需要对偏差e进行累加求和,每次输出均与以前的状态相关,计算时需要对e(k)进行累加,工作量比较大。为了避免初次启动造成瞬间微分值过大的缺点,本研究采用监看测定值(PV)的微分状况,PID指令控制框图如图3所示。

图3 PID指令控制框图
则PID表达式为:
(13)
式中:u(k)—输出值;uSV(k)—目标值;uPV(k)—测定值。
PID控制原理是将输入值SV与测定值PV偏差e输入PID控制器中,设定PID控制中的KP,KI,KD3个参数,对直流电机进行调速[12-13]。
该指令采用监看测定值PV的微分状况,当测定值PV变化量过大时,即车轮速度变化量过大时,则将会降低输出值MV的输出,从而以PWM波的形式输出对电机进行调速。
PLC作为控制器,通过其内部PID处理器,将输入输出信号进行AD转换。基于PLC的PID指令,首先要进行参数初始化,在指定时间点上向模拟量取值,取出模拟量后,需要采用模拟量输入(A/D)转换模块进行模拟量输入,最后通过模拟量输出模块(D/A)输出或采用PWM波形输出[14]。
3 仿真与实验分析
3.1 仿真模型建立
根据图2可知,直流电机PWM调速环节的传递函数为[15]:
(14)

直流电机经PWM调速后的转速与输入电压传递函数为:
(15)
式中:Ce—电动势常数,0.2;Tm—电气传动时间常数,0.009 8;T1—时间常数,L/R∑;L—电枢回路总电感,0.18 mH;R∑—电枢回路总电阻,0.18 Ω。
PID环节传递函数为:
(16)
直流电机PID调速控制系统闭环传递函数为:
(17)
式中:α—反馈系数,0.015 V·min/r。
3.2 系统仿真及分析
系统仿真的思想是根据直流电机PID调速控制系统的传递函数,考查在不同PID参数下其响应曲线特征规律。
PID参数采用临界比例度法[16],按照P-I-D环节操作顺序,整定参数。PID参数调节过程及AGV运行轨迹如图4所示。

图4 PID参数调节过程及AGV运行轨迹
经Matlab仿真,在参数整定后得到的理想的AGV纠偏阶跃响应曲线如图5所示。

图5 AGV纠偏阶跃响应
由图5可知:KP=4 000,KI=10,KD=1时,系统响应快速、性能稳定,无超调、无振荡,调节时间约为3 s,满足纠偏性能要求。
根据式(4,8),对直流电机进行纠偏调速,可得到AGV轨迹仿真曲线,如图6所示。

图6 AGV轨迹仿真曲线及实验原理图
图6中,AGV以(0,0)点为起始点,直线距离为3 m,弯道半径为1.5 m的环形跑道进行行驶,该仿真轨迹基本与标准轨迹重合,满足纠偏要求。
3.3 实验测试与分析
图6中,磁条轨迹与AGV构成了系统测试方案,在模拟作业区铺设磁条轨迹,复合机器人沿着磁条轨迹进行试运行。
为进一步分析调节参数对电机调速的影响,笔者让AGV沿着固定轨迹进行连续行驶,在AGV运行轨迹上设置4个检测点,并分别在4个检测点粘贴白纸,使白纸的中心位置与磁条的中心位置重合,以蓝线标识。AGV沿着磁条运行,当运行到检测点时,固定在车体中心处的记号笔将会在白纸上留下AGV运行痕迹,并检测实际轨迹与理想轨迹的偏差距离,以磁条中心线右侧的偏差为正。
现场实际运行测试如图7所示。

图7 现场模拟运行实验测试照片
图7中右上角给出了AGV轨迹上4个点的实验纠偏检测结果分布情况。当KP过小时,实际轨迹偏差较大;当KP=4 000时,实际轨迹偏差较小。
不同调节参数下AGV上某固定点与标准轨迹间的偏差Δx测试如表1所示。
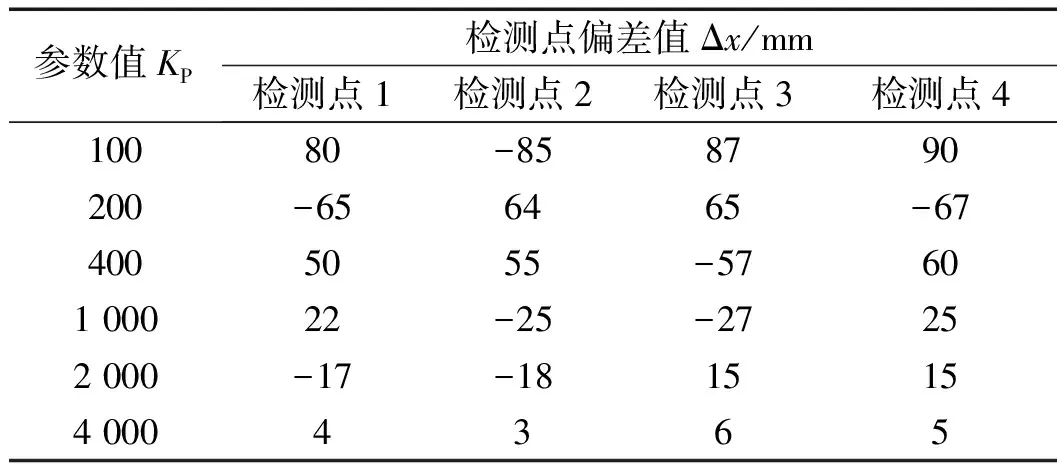
表1 AGV偏差距离表
由图7以及表1可以看出:当KP=4 000时,经过多次实验,检测到在检测点的偏差平均值在±10 mm以内,满足AGV的定位要求,同时根据实际AGV行驶路径以及仿真路径发现,AGV运行轨迹与标准轨迹基本一致。
4 结束语
针对纺织车间棉桶搬运自动化问题,本文提出了复合机器人及配套技术总体解决方案:
(1)针对复合机器人纠偏调速问题,本文建立了其基于轨迹跟踪系统运动学模型,运用Matlab软件进行了仿真,结果表明:AGV运行轨迹与标准轨迹基本重合,验证了基于轨迹跟踪系统运动学建模方法的正确性;
(2)针对直流电机PWM调速方式,本文给出了基于PID控制的直流电机脉宽调速方法,建立了系统数学模型,采用Matlab进行了仿真。结果显示:纠偏过程无超调、无振荡、调节速度快;对现场实验测试表明:复合机器人运行轨迹上检测点的偏差<±10 mm,满足AGV定位精度要求。
现场运行过程发现,AGV能够平稳运行,可以实现自主导航以及纠偏功能,纠偏效果较好,可以完成定点停靠以及棉桶的搬运工作。
