波动转矩下渐开线直齿轮传动齿廓修形研究

王 成，刘 辉，项昌乐

（北京理工大学机械与车辆学院，北京 100081）

波动转矩下渐开线直齿轮传动齿廓修形研究

王 成，刘 辉，项昌乐

（北京理工大学机械与车辆学院，北京 100081）

分析了齿轮转速波动和齿面、齿背啮合相位差对啮合点的影响，结合单、双齿啮合和修形边界条件并采用解析法计算啮合刚度，建立了与齿轮实际运动状态和啮合状态相关的非线性啮合刚度模型，该模型可与齿轮非线性动力学方程实时反馈，更加准确地描述齿轮传动过程中的啮合刚度。建立了考虑间隙、非线性啮合刚度的2自由度单级齿轮传动非线性动力学模型，在波动转矩的作用下，对比研究齿廓修形参数对齿轮动态特性的影响。研究结果表明：修形量对齿轮动态特性影响显著，存在最优修形量使动载系数达到最小；当修形量超过某临界值齿轮产生单边或双边冲击现象，齿轮动载荷明显增加；外载荷一定，增加修形长度可降低动载系数最小值；波动转矩作用下，齿轮的最大修形量为最小转矩作用下单齿啮合最高点的变形量。

齿轮传动；齿廓修形；啮合刚度；冲击

随着齿轮传动系统向着高速、重载方向发展，在内、外激励共同作用下齿轮传动系统的振动和噪声加剧，严重影响齿轮传动系统的可靠性。修形是降低齿轮传动系统振动、噪声和提高可靠性的关键技术，齿轮修形包括齿高方向的齿廓修形和齿宽方向的齿向修形两方面，其中，齿廓修形是应用最为广泛的一种修形方式。齿廓修形可有效地缓和啮合齿数变化时引起的啮合刚度急剧变化，从而减小啮合初始冲击，降低齿轮传动系统的振动和噪声［1］。

国内外学者对齿廓修形技术做了深入研究。Tavakoli等［2］研究了齿廓修形参数对齿轮静态传递误差（STE）的影响并进行优化设计。Chen等［3］考虑修形、齿形误差等因素，研究了齿廓修形对啮合刚度和齿间载荷分配系数的影响。蒋进科等［4］开展了以承载传动误差幅值、啮入冲击力与啮合线向加速度均方根最小为目标的齿轮修形优化设计。孙月海等［5］考虑误差等因素研究了定载荷作用下的齿廓修形准则。朱才朝等［6］基于静态修形以改善啮合性能，并对修形结果进行了试验验证。Bonori等［7］研究了静态传递误差峰峰值最小时对应的最优齿廓修形参数，并基于非线性动力学模进行仿真验证。唐增宝和朱传敏等［8－9］考虑误差和周期时变刚度等因素建立了齿轮非线性动力学模型，研究了齿轮动态性能最优时对应的最佳齿廓修形参数。Lin等［10］基于考虑周期时变啮合刚度的线性时变齿轮动力学模型，研究了齿廓修形对齿轮系统动载荷的影响。Liu和郭家舜等［11－12］考虑周期时变刚度、间隙等因素建立了的齿轮动力学方程，研究了齿廓修形对齿轮系统动态传递误差的影响。Marcello等［13］基于考虑周期时变刚度、间隙等因素的非线性动力学模型，采用优化设计的方法研究了动态传递误差最小时对应的齿廓修形参数。

以往基于齿轮动态特性的齿廓修形研究中［8－13］，啮合刚度模型均采用静态或准静态的方法获得，啮合刚度呈现出周期时变特性。实际上，齿轮传动过程中的啮合刚度不仅与修形参数有关还与齿轮实际运动状态和啮合状态相关，例如齿轮波动转速，齿面、齿背啮合状态变化等。本文考虑了齿轮转速波动和齿面、齿背啮合相位差对啮合点的影响，结合解析法计算啮合刚度，建立了与齿轮实际运动状态和啮合状态相关的非线性啮合刚度模型，该模型可与齿轮非线性动力学方程实时反馈。建立了考虑间隙、非线性啮合刚度模型以及波动转矩的2自由度单级齿轮传动非线性动力学模型。在动力学模型的基础上，首先，对比分析了修形量、修形长度对齿轮动态特性的影响规律，最后，提出了波动转矩作用下最大修形量的选取准则。

1 单级齿轮传动非线性动力学模型

假设齿轮传动的扭转模态对应的固有频率远离齿轮中心支撑大变形模态对应的固有频率，齿轮的中心位置可视为刚性支撑［14］。图1为单级齿轮传动扭转动力学模型，J1，J2和θ1，θ2分别为齿轮1和齿轮2的转动惯量和扭转自由度；rb1和rb2分别为齿轮1和齿轮2的基圆半径；ct1和ct2分别为齿轮1和齿轮2的扭转阻尼系数；T1和T2分别为齿轮1和齿轮2的驱动力矩和负载力矩；b为单边齿侧间隙；α为齿轮副啮合角；齿轮副通过沿着啮合线AB方向的啮合刚度km和啮合阻尼cm耦合在一起。

单级齿轮传动的动态传递误差（DTE）Δ为

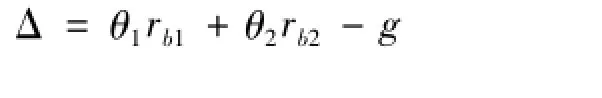
图1 单级齿轮传动扭转动力学模型Fig.1 Dynamicmodel of spur gear pair

式中：g为修形和轮齿制造误差等引起的齿形偏差。

单级齿轮传动非线性动力学方程为

式中：km为非线性啮合刚度模型（详细分析见第2节），cm为啮合阻尼，f（b，Δ），f1（b，Δ）分别为间隙和速度非线性函数［15］。

由于间隙的存在，齿轮可能产生三种啮合状态：齿面啮合、脱齿和齿背啮合。脱齿产生时，齿轮为单边冲击；齿背啮合产生时，齿轮为双边冲击，如图2所示。

图2 间隙非线性函数Fig.2 Nonlinear backlash function

2 非线性啮合刚度模型

计算齿轮传动过程中任意时刻齿轮副的啮合刚度，首先应确定任意时刻啮合点的位置。

2.1 任意时刻啮合点的位置

齿面啮合状态，啮合点压力角与齿轮1转速的关系如图3所示，固定坐标系o1xy如图1所示。对齿轮副啮合点P进行瞬时速度分析。旋转坐标系o1εη的中心在齿轮1中心位置且随齿轮1旋转，啮合点P为动点。由速度分析可得啮合点压力角α1i与齿轮转速ω1之间满足

式中：α10为常数，为初始啮合位置啮合点压力角。

图3 啮合点压力角与齿轮1转速的关系Fig.3 Relationship between mesh point pressure angle and rotation speed

若齿轮处于齿背啮合状态，齿轮1的位置不变，齿面、齿背啮合点的压力角之间存在相位差［16］，如图4所示，其中虚线代表齿背啮合状态的啮合线。

图4 齿面、齿背啮合状态啮合点压力角Fig.4 Relationship between pressure angles of backside and frontside contact

2.2 单、双齿啮合与修形区边界条件

判断单齿啮合和双齿啮合条件，需确定αa、αb、αc和αd四个参数，如图5所示。同一齿轮各轮齿的单、双齿啮合边界条件相同，其中，αa为齿顶圆压力角，αd由几何关系可得

如果轮齿存在齿廓修形，在单、双齿啮合边界条件的基础上需要增加修形区边界条件，如图6所示。α1

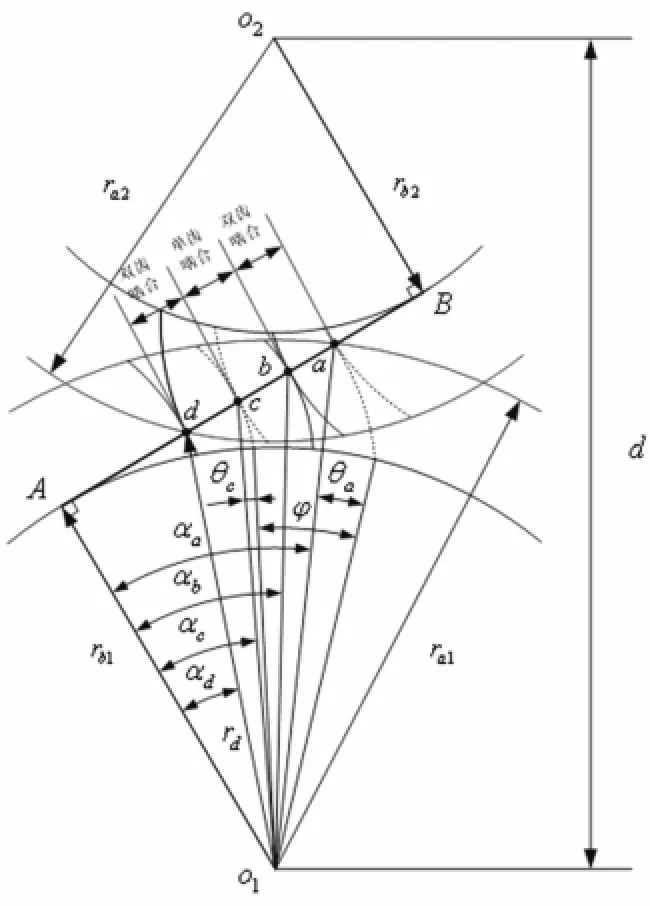
图5 单、双齿啮合边界条件Fig.5 Boundary conditions of single-tooth-meshing and double-tooth-meshing

为齿轮1的修形区边界条件，等于修形起始点的压力角，α1与修形长度L相关，C为修形量。当齿轮啮合进入齿轮2的修形区，由几何关系可得另一个边界条件α2

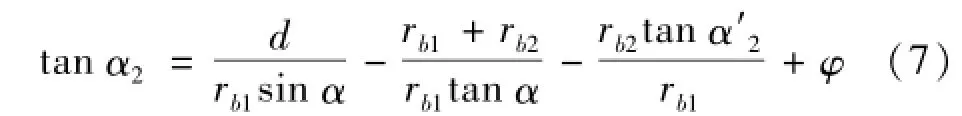
式中：α′2为齿轮2修形起始点的压力角，与齿轮2的修形长度相关。

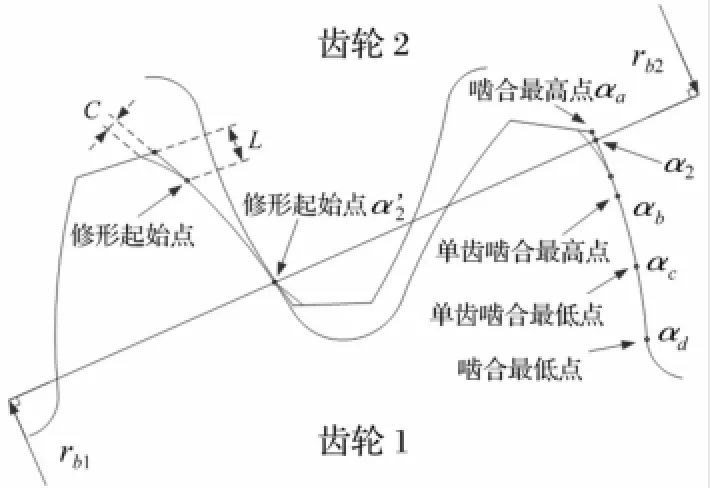
图6 修形区边界条件Fig.6 Boundary conditions of profilemodification area

2.3 非线性啮合刚度模型

结合2.1节和2.2节分析得到的啮合点位置和单、双齿啮合与修形区边界条件，并采用解析法计算啮合刚度，提出非线性啮合刚度模型km

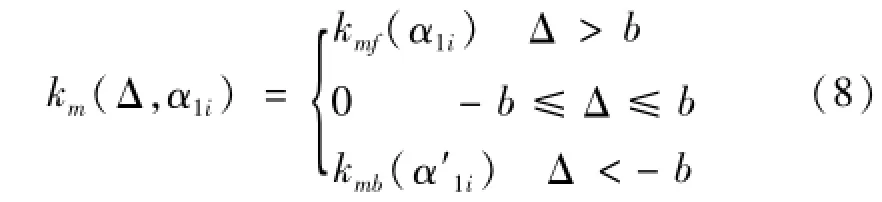
式中：α1i与齿轮的波动转速相关（式（1）），α′1i为α1i的函数（式（3）），kmf、kmb分别为齿面、齿背啮合状态的啮合刚度，它们均与啮合点的位置相关，为啮合点压力角的函数。

式中：ks为单齿啮合区的单对齿啮合刚度，ks1，ks2分别为双齿啮合区不同齿对的单对齿啮合刚度，修形区的啮合刚度kmp，采用文献［3］方法计算。

本文采用解析法计算单对齿啮合刚度ks

式中：δB为轮齿本身的变形，采用Weber法并结合Cornell的判断条件计算［17－18］；δM为轮体的附加变形，采用二维解析计算模型计算［19］；δC为轮齿之间的接触变形，采用赫兹接触模型计算［20］。

单级齿轮传动非线性动力学方程仿真流程如图7所示。

图7 单级齿轮传动非线性动力学方程仿真流程Fig.7 Numerical simulation flowchart of nonlinear dynamic model of spur gears

3 修形对齿轮传动动态特性的影响

不失一般性，为了便于齿轮加工，采用线性修形即关于渐开线展角的线性函数。对齿轮进行齿根修形相当于对相啮合齿轮的齿顶进行修形，且齿根修形会减弱齿根的强度［1］，因此仅对轮齿进行齿顶修形。

采用4阶定步长龙格库塔法求解单级齿轮传动的非线性动力学方程。单级齿轮传动参数如表1所示。

表1 单级齿轮传动参数Tab.1 Parameters of spur gear pair

3.1 修形参数对齿轮传动动态特性的影响

单级齿轮传动的输入转速为2 000 r/min，输入转矩为T1＝500＋100sin（200πt）Nm，初始啮合状态为齿面啮合并从齿轮2的齿顶进入啮合。各齿轮齿面、齿背修形参数相同。

在修形长度一定的情况下，分析修形量对齿轮传动动态特性的影响。修形长度为1 mm，修形量为0～0.1 mm，取值间隔为0.002 mm，其中，修形量为0代表齿轮无修形。齿轮动载系数随修形量的变化规律如图8所示。随着修形量的增加，动载系数的变化趋势呈现‘V’型，存在最优修形量使得齿轮的动载系数达到最小，对应的修形量为0.022 mm，最小动载系数为1.548。当轮齿修形量大于0.042 mm，齿轮的动载系数超过无修形齿轮的动载系数2.364。当修形量超过0.088 mm，齿轮动载系数存在较大的跳跃，较无修形齿轮动载系数增加一倍左右，齿轮传动动载荷明显增加，由后面的分析可知该修形区间内齿轮产生双边冲击。

齿轮动态传递误差峰峰值随修形量的变化规律如图9所示。随着修形量的增加，动态传递误差峰峰值变化趋势呈现‘V’型，动态传递误差峰峰值达到最小所对应的修形量为0.006 mm，该值小于动载系数达到最小所对应的修形量0.022 mm。当轮齿修形量大于0.012mm，修形齿轮动态传递误差峰峰值大于无修形齿轮的动态传递误差峰峰值。当修形量超过0.088 mm，齿轮的动态传递误差峰峰值同样存在较大的跳跃。

图10为齿轮动态传递误差最大值、最小值随修形量的变化规律。当修形量在0～0.048 mm之间，齿轮动态传递误差最小值大于单边齿侧间隙0.05 mm，齿轮始终保持啮合状态并不存在冲击现象。当修形量在0.048 mm～0.088 mm之间，齿轮的动态传递误差最小值小于单边齿侧间隙0.05 mm，齿轮产生单边冲击。进一步增加修形量到0.088 mm～0.1 mm之间，动态传递误差最小值小于－0.05 mm，齿轮产生双边冲击，这是造成图8中动载系数存在较大跳跃的主要原因。结合图8和图9，当齿轮的修形量大于0.048 mm，修形齿轮产生单边或双边冲击，齿轮的动载系数较大，且大于无修形齿轮的动载系数。综上所述，修形量的大小对齿轮传动的动态特性影响显著，存在最优修形量使得齿轮的动载系数达到最小。存在某临界修形量，当修形量超过该临界值，齿轮传动产生单边或双边冲击现象，此时齿轮动载荷较无修形齿轮动载荷明显增加。

图8 动载系数随修形量的变化规律Fig.8 Influence of amount of modification on dynamic load factor

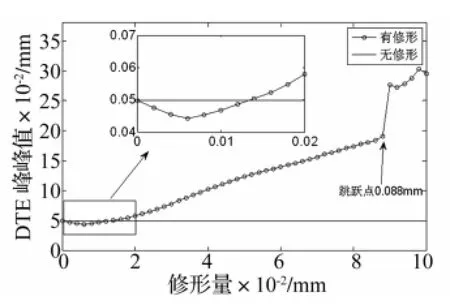
图9 动态传递误差峰峰值随修形量的变化规律Fig.9 Influence of amount of modification on peak to peak value of dynamic transmission error

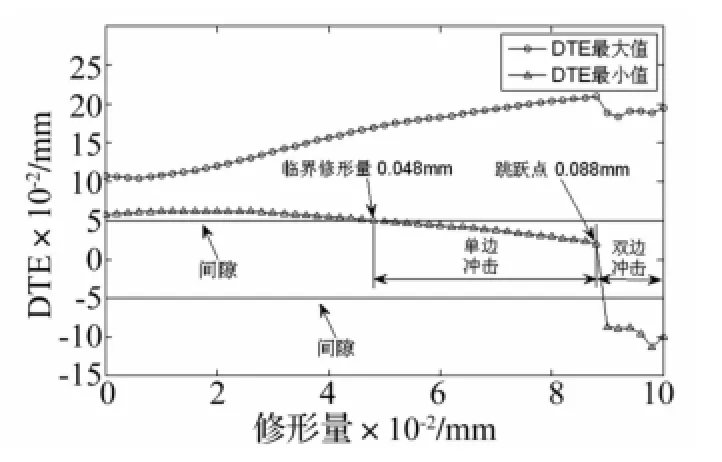
图10 动态传递误差最大值、最小值随修形量的变化规律Fig.10 Influence of amount ofmodification on maximum and minimum value of dynamic transmission error

修形量分别为0.006mm和0.022 mm的修形齿轮与无修形齿轮的啮合刚度、啮合力和动态传递误差时域对比结果分别如图11，图12和图13所示，其中，0.006 mm为动态传递误差峰峰值最小时对应的修形量，0.022 mm为动载系数最小时对应的修形量。由图11可以看出，无修形齿轮啮合刚度在单、双齿啮合过渡时刻，啮合刚度变化明显具有阶跃性，修形齿轮的啮合刚度在单、双齿过渡时刻，啮合刚度的阶跃特性均明显缓和，其中，修形量为0.022 mm的修形齿轮的缓和效果更为明显。由图12可以看出，修形齿轮的啮入冲击载荷显著降低，两种修形量下修形齿轮的啮合力最大值较无修形齿轮啮合力最大值分别降低了11.2%和 34.5%。由图13可以看出，修形齿轮和无修形齿轮相比，双齿啮合区内动态传递误差的波动范围降低，单齿啮合区内动态传递误差增加，结合图12可以看出，修形齿轮在单齿啮合区的啮合力也随之增加。结合图12和图13可知，与修形量为0.006 mm的修形齿轮相比，修形量为0.022 mm的修形齿轮的最大啮入冲击载荷明显降低，但单齿啮合区的啮合力有所增加导致动态传递误差增加。因此，0.022 mm不是动态传递误差峰峰值最小时对应的修形量，而0.006 mm是动态传递误差最小时对应的修形量但最大啮入冲击载荷并非最小，从而导致动载系数最小时对应的修形量与动态传递误差峰峰值最小时对应的修形量存在差别。

图11 啮合刚度时域曲线Fig.11 Time domain response ofmesh stiffness

图12 啮合力时域曲线Fig.12 Time domain response of gearmesh force

图13 动态传递误差时域曲线Fig.13 Time domain response of dynamic transmission error

下面分析修形长度对单级齿轮动态特性的影响，针对表1中齿轮，单齿啮合最高点（如图6所示）对应修形长度为L＝2.67 mm。本文修形长度取值均小于最大修形长度，即修形起始点高于单齿啮合最高点，L1＝1 mm，L2＝1.5 mm，L3＝2.0 mm和L4＝2.5 mm。

图14和图15分别为不同修形长度齿轮动载系数随修形量的变化规律。随着修形长度的增加，动载系数达到最小的最优修形量无明显的变化，分别为0.022 mm和0.02 mm，对应动载系数最小值逐渐降低，分别为1.547，1.47，1.335和1.229。当修形长度为2 mm，齿轮动载系数随修形量的变化趋势较其它3种情况平缓并不存在跳跃现象，由图16可知，该修形量0～0.1 mm区间内齿轮并没有发生双边冲击。进一步放大如图17所示，对于前三种情况，随着修形长度的增加，临界修形量也相应增加，当轮齿修形长度为2.5 mm，临界修形量反而降低，且小于前三种情况。

图14 不同修形长度齿轮动载系数随修形量的变化规律Fig.14 Influence of amount ofmodification on dynamic load factor with different length ofmodification

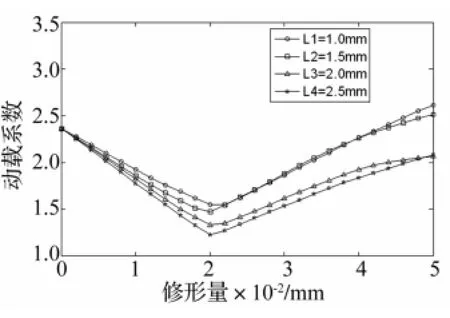
图15 不同修形长度齿轮动载系数随修形量的变化规律（局部放大）Fig.15 Influence of amount ofmodification on dynamic load factor with different length ofmodification（enlarged）

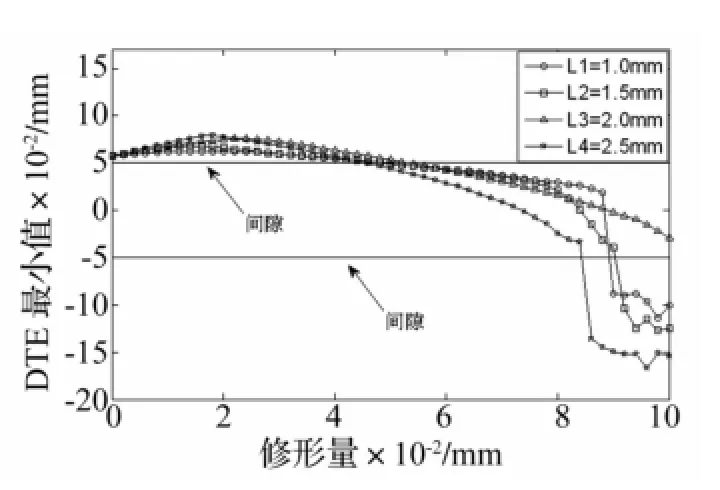
图16 不同修形长度齿轮动态传递误差最小值随修形量的变化规律Fig.16 Influence of amount ofmodification onm inimum dynamic transmission error with different length ofmodification

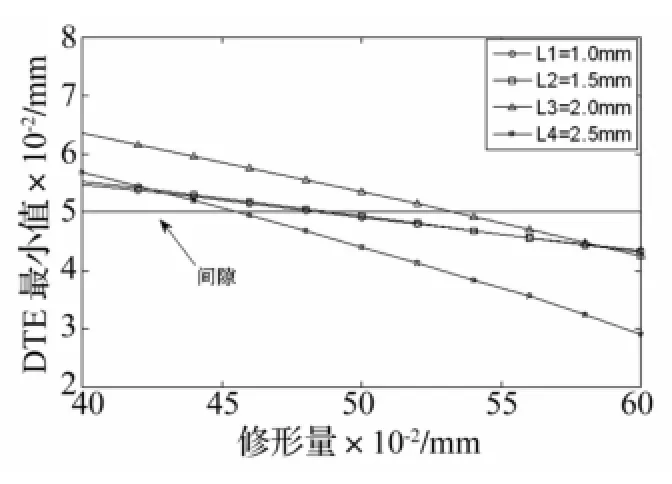
图17 不同修形长度齿轮动态传递误差最小值随修形量的变化规律（局部放大）Fig.17 Influence of amount ofmodification onminimum dynamic transmission error with different length ofmodification（enlarged）

图18 不同波动转矩下齿轮动载系数随修形量的变化规律Fig.18 Influence of amount of modification on dynamic load factor with different fluctuation torque

图19 不同波动转矩下动载系数随修形量的变化规律（局部放大）Fig.19 Influence of amount ofmodification on dynamic load factor with different fluctuation torque（enlarged）

3.2 不同波动转矩下修形量对齿轮动态特性的影响

本节研究不同波动转矩下修形量对齿轮动态特性的影响。单级齿轮传动的输入平均扭矩为500 Nm，波动转矩分为三种情况：第一种情况，波动转矩为平均转矩的0%；第二种情况，波动转矩为平均转矩的20%；第三种情况，波动转矩为平均转矩的40%，即波动转矩分别为0 Nm，100 Nm和200 Nm。齿轮传动的输入转速，初始啮合状态与3.1节相同，修形长度均取为1 mm。

不同波动转矩下齿轮动载系数随修形量的变化规律如图18所示。同等修形量下齿轮的动载系数随着波动转矩的增加而增加。不同波动转矩下，动载系数随修形量的变化均呈现‘V’型变化。当波动转矩为平均转矩的40%，动载系数发生跳跃变化对应的修形量为0.07 mm，低于前两种情况对应的修形量0.088 mm，动载系数的跳跃变化均由双边冲击引起。进一步放大图像如图19，随着波动转矩的增加，齿轮动载系数最小对应的最优修形量逐渐增加分别为0.018 mm，0.022 mm和0.024 mm，动载系数分别为1.328，1.548和1.725。

图20为不同波动转矩下齿轮动态传递误差最小值随修形量的变化规律。当波动转矩为平均转矩的40%，齿轮双边冲击产生对应的最小修形量小于前两种情况。进一步放大图像如图21，随着波动转矩的增加，造成齿轮产生单边或双边冲击的临界修形量逐渐降低。

图20 不同波动转矩下动态传递误差最小值随修形量变化规律Fig.20 Influence of amount ofmodification on minimum dynamic transmission error with different fluctuation torque

以往的研究中，最大修形量选取准则多采用两种方法。第一种方法，在一些修形的准则中最大修形量推荐为［3］，Cmax＝0.02 m，其中m代表模数。第二种方法，最大修形量选择为定常设计载荷作用下单齿啮合最高点的变形［10］。

以本文研究的单级齿轮传动为例，采用第一种方法选取最大修形量Cmax＝0.06 mm。由图18和图21可知，三种波动转矩作用，该修形量对应的齿轮传动均产生了单边冲击现象，齿轮传动动载系数较大，且大于无修形齿轮的动载系数。采用第二种方法选取最大修形量，当齿轮传动输入转矩无波动（第一种情况）单齿啮合最高点的变形为：Cmax＝0.048 mm，该修形量对应的动载系数小于修形量0.06 mm对应的动载系数。对于第二种和第三种波动转矩情况，齿轮1上分别施加最小转矩Tmin，平均转矩Tmean，最大转矩Tmax。第二种情况，单齿啮合最高点的变形分别为：Cmax1＝0.038 mm，Cmax2＝0.048 mm，Cmax3＝0.058 mm；第三种情况，单齿啮合最高点的变形分别为：Cmax1＝0.028 mm，Cmax2＝0.048 mm，Cmax3＝0.068 mm。若采用Cmax3作为修形量，两种波动转矩下修形齿轮会产生单边冲击，齿轮动载荷较大。采用Cmax2作为修形量，尽管两种波动转矩下齿轮均没有发生单边或双边冲击现象，但齿轮的动载荷仍较大。采用Cmax1作为修形量，两种波动转矩下齿轮的动载荷均较小，且最优修形量均小于Cmax1。因此，在针对波动转矩作用下的齿轮传动系统进行齿廓修形研究和优化设计，最大修形量为理论最小转矩作用下单齿啮合最高点的变形量。

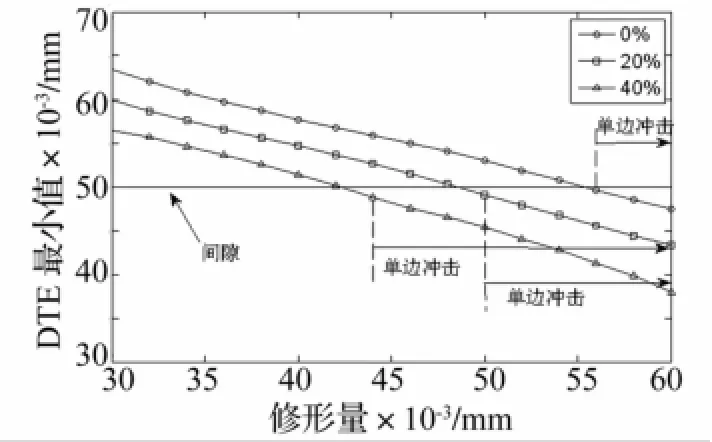
图21 不同波动转矩下动态传递误差最小值随修形量变化规律（局部放大）Fig.21 Influence of amount ofmodification on minimum dynamic transm ission error with different fluctuation torque（enlarged）

4 结 论

（1）考虑齿轮转速波动，齿廓修形和齿面、齿背啮合相位差，结合解析法计算啮合刚度，建立了与齿轮实际运动状态和啮合状态相关的非线性啮合刚度模型，该模型可与齿轮非线性动力学方程实时反馈，更加准确地描述了齿轮传动过程中的啮合刚度。

（2）修形量的大小对齿轮的动态特性影响显著，存在最优修形量使得齿轮传动动载系数达到最小，但与动态传递误差峰峰值最小时对应的修形量存在差别。

（3）存在临界修形量，当修形量超过该临界值，齿轮传动产生单边或双边冲击现象，齿轮的动载荷增加，双边冲击产生时动载系数增加显著。

（4）外载荷一定，增加修形长度可降低动载系数最小值。

（5）随着波动转矩的增加，动载系数达到最小时的最优修形量逐渐增加，而齿轮产生单边或双边冲击的临界修形量逐渐降低。

（6）波动转矩作用下，齿轮的最大修形量为最小转矩作用下单齿啮合最高点的变形量。

［1］仙波正驻.高强度齿轮设计［M］.北京：机械工业出版社，1981.

［2］TavakoliMS，Houser D R.Optimum profilemodifications for the m inimization of static transmission errors of spur gears［J］.Journal ofMechanisms Transmissions and Automation in Design，1986，108：86－95.

［3］Chen Z G，Shao Y M.Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack［J］.Mechanism and Machine Theory，2013，62：63－74.

［4］蒋进科，方宗德，王峰.降低斜齿轮噪声的对角修形优化设计［J］.振动与冲击，2014，33（7）：63－67.

JIANG Jin-ke，FANG Zong-de，WANG Feng.Optimal design with diagonalmodification for reducing helical gear noise［J］.Journal of Vibration and Shock.2014，33（7）：63－67.

［5］孙月海，张策，葛楠.含误差的直齿轮的齿廓修形［J］.机械工程学报，2009，39（12）：91－94.

SUN Yue-hai，ZHANG Ce，GE Nan.Tooth profile modification for spur gear with manufacturing error［J］.Chinese Journal of Mechanical Engineering，2009，39（12）：91－94.

［6］朱才朝，陈爽，马飞，等.轮齿修形对兆瓦级风电齿轮箱动态特性影响［J］.振动与冲击，2013，32（7）：123－128.

ZHU Cai-chao，CHEN Shuang，MA Fei，et al.Effect of gear teeth modification on dynamic characteristics of a megawatt level wind turbine gearbox［J］.Journal of Vibration and Shock.2013，32（7）：123－128.

［7］Bonori G，Barbieri M，Pellicano M.Optimum profile modifications of spur gears by means of genetic algorithms［J］.Journal of Sound and Vibration，2008，313（3）：603－616.

［8］唐增宝，钟毅芳，陈久荣.修形齿轮的最佳修形量和修形长度的确定［J］.华中理工大学学报，1995，23（2）：125－128.

TANG Zeng-bao，ZHONG Yi-fang，CHEN Jiu-rong.Determination of the optimum modifieative number and length for gear profile［J］.Journal of Huazhong University，1995，23（2）：125－128.

［9］朱传敏，宋孔杰，田志仁.齿轮修形的优化设计与试验研究［J］.机械工程学报，1998，34（4）：63－68.

ZHU Chuan-min，SONG Kong-jie，TINA Zhi-ren.Optimum design and experiment study on the gear profile modification［J］.Chinese Journal of Mechanical Engineering，1998，34（4）：63－68.

［10］Lin H H，Oawale F B，Townsend D P.Dynamic loading of spur gears with linear or parabolic tooth profile modifications［J］.Mechanism and Machine Theory，1994，29（8）：1115－1129.

［11］Liu G，Parker R G.Dynamic modeling and analysis of tooth profilemodification formultimesh gear vibration［J］.Journal of Mechanical Design，2008，130：1－13.

［12］郭家舜，王三民，王颖.基于解析解的人字齿轮齿廓修形动态分析［J］.航空动力学报，2013，28（3）：613－620.

GUO Jia-shun，WANG San-min，WANG Ying.Dynamic analysis of tooth profile modification to heeringbone gears based on analytical solutons［J］.Journal of Aerispace Power，2013，28（3）：613－620.

［13］Marcello F，Farhad S S，Gabrieie B，et al.Dynamic optimization of spur gears［J］.Mechanism and Machine Theory，2011，46：544－557.

［14］Eritenel T，Parker R G.Nonlinear vibration of gears with tooth surface modifications［J］.Journal of Vibration and Acoustics，2013，135：1－11.

［15］李润方，王建军.齿轮系统动力学［M］.北京：科学出版社，1997.

［16］Chen Z G，Shao Y M，Lin T C.Nonlinear dynamic simulation of gear response under the idling condition［J］.International Journal of Automotive Technology，2012，13：541－552.

［17］孙甜甜.车辆动力传动轴系弯扭耦合振动特性研究［D］.北京：北京理工大学，2009.

［18］Cornell R W.Compliance and stress sensitivity of spur gear teeth［J］，Journal of Mechanical Design，1981，103：447－458.

［19］Sainsot P，Velex P，Duverger O.Contribution of gear body to tooth deflections-a new bi-dimensional analytical formula［J］.Journal of Mechanical Design，2004，126：748－752.

［20］Chen ZG，Shao Y M.Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth［J］.Engineering Failure Analysis，2011，18：2149－2164.

In fluences of p rofilem odification on dynamic characteristics of involute spur gears under a fluctuating torque

WANGCheng，LIU Hui，XIANGChang-le
（School ofMechanical and Vehicular Engineering，Beijing Institute of Technology，Beijing 100081，China）

The influences of rotating speed fluctuation and the phase shift between forward and backward contact on mesh point position were analyzed.Combining boundary conditions of single-tooth meshing，double-tooth meshing，and profilemodification and using the analytical method to calculate mesh stiffness，a nonlinear mesh stiffness model was established to achieve a real-time feedback with the nonlinear dynamic model of spur gears and produce a more precise mathematicalmodel of gear meshing process.A 2-DOF nonlinear dynamic model of a spur gear pair with input torque fluctuation was established by taking backlash and nonlinearmesh stiffness into account.Based on the nonlinear dynamic model，the influence ofprofilemodification on the dynamic behavior of the spur gear pairwas studied.The resluts showed that the amountof profilemodification significantly affects the dynamic characteristics of the spur gear pair，and an optimal amount of profile modification exists to make the dynamic load factor reach the minimum；when the amount of profile modification exceeds a certain critical value，single-side-impact or double-side-impact occurs and the gear dynamic loads significantly increase；increasing the length of profile modification can reduce the minimum value of the dynamic load factor under a certain input torque；themaximum amount of profilemodification should be the combined tooth deformation at the highest point of single tooth contact under the minimum input torque.

gear transmission；profilemodification；mesh stiffness；impact

TH132

A

10.13465/j.cnki.jvs.2014.24.006

国家自然科学基金资助项目（51375047）；教育部新世纪优秀人才支持计划资助（NCET－12－0043）

2014－05－29 修改稿收到日期：2014－08－14

王成男，博士生，1987年生

刘辉女，博士，教授，博士生导师，1975年生