距离徙动算法研究

刘志鹏

(中国电子科技集团公司电子科学研究院，北京 100041)

0 引 言

距离徙动算法(RMA)又称为波数域(ω-k)算法，起源于地震信号处理邻域，由Cafforio等人提出[1]。后经人们的发展，将距离徙动算法应用于条带SAR和聚束SAR[2]。可以说，RMA算法一经提出，就引起了人们的极大兴趣，因为它采用了较少的近似，成像结果较好，因而被认为是最优的算法[3]。最优体现在两点，一是与反向投影(BP)算法相比，它的运算量少；二是与二次距离压缩(SRC)算法[4]、线性调频(CS)算法[5]以及非线性调频(NCS)算法[6]等相比，它的近似最少。但是RMA算法相对于SRC算法、CS算法而言，运算量不占优势，故有了RMA算法后，仍然需要研究其他的成像算法。

本文的结构如下：在第二部分，本文给出了在SAR领域应用最为广泛的斜距模型，并指出了适用的情况；在第三部分，本文推导了非Dechirp下的信号波数谱；在第四部分，本文详细推导了Dechirp和非Dechirp下的RMA算法，并给出了各自的流程图。在该部分本文还详细解释了STOLT插值原理，并通过与其他经典成像算法所用的二维频谱的对比得出了RMA算法是最优的一种成像算法；在第五部分，本文主要对非Dechirp下和Dechirp下的成像算法做了仿真验证，仿真结果证明了成像算法的有效性；最后，本文做了总结。

1 斜距模型

在SAR成像处理领域，一般有两个假设：等效直线模型假设和“Stop-and-Go”假设。所谓等效直线模型指的是认为卫星的飞行的轨迹可以用一条直线来近似。“Stop-and-Go”假设是指卫星每次发射完信号后，近似认为是不动的直到卫星接收完反射回来的信号(即回波)才移动到下一位置再次发射信号。在这两个假设下，就可以建立SAR斜距。

在SAR领域一般有三种斜距的写法，

(1)

(2)

(3)

其中，R为卫星与目标的最短斜距，v为卫星的速度，ta为方位向时间，θ为斜视角。

一般来说，公式(1)多用于正侧视，公式(2)和(3)用于斜视。当公式(1)用于斜视时，它与(2)和(3)的区别在于方位向时间起点的选取不一样。公式(2)用于泰勒展开定性分析误差比较方便，用于推导信号的二维频谱表达式比较复杂。公式(3)用于求回波信号的二维频谱比较方便。本文中采用公式(1)来推导Dechirp下的RMA算法，用公式(3)来推导非Dechirp下的RMA算法和回波信号的二维波数域或二维频域的表达式。不过需要指出的是，以上三种斜距的写法从本质上说是一致的。

2 信号波数谱

为了后续处理的方便，我们首先推导一下非Dechirp下的SAR信号的二维波数谱。首先，信号回波模型为

(4)

这里忽略了幅度的影响。其中，tr、ta分别是距离向和方位向时间，β是距离向调频率，c为光速，λ为波长，r(ta)为目标斜距历史，表达式为

(5)

其中θ为斜视角，R为波束中心照射到点目标时的斜距。

距离向FFT后，可以得到

(6)

其中，fr为距离向频率，KR为垂直于航迹的波数，

(7)

这里，fc为雷达中心频率。

方位向FFT，可以得到回波的二维波数域表达式，

(8)

其中，KX为沿航迹的波数，

(9)

这里fa为方位向频率。

3 成像算法处理

RMA算法既可以采用Dechirp的方法也可以采用非Dechirp的方法来处理。Dechirp和非Dechirp的方法从距离压缩的角度来说，本质是一致的。但是Dechirp的方法有利于降低采样率，在合成孔径激光雷达(SAL)中应用的较为广泛。

3.1 非Dechirp处理方法

非Dechirp方法首先对(6)进行距离向压缩，其补偿函数为

H1=[FFT{sref(tr)}]*

(10)

其中，

(11)

为了能够处理斜视情况下，在方位向FFT之前补偿下面的相位，

H2=exp(-j·2·π·fdc·ta)

(12)

其中，fdc为多普勒中心。

在二维波数域，进行匹配滤波，去除

sinθ·KX-j·Rs·KR)

(13)

在二维频域进行STOLT插值，即

(14)

插值前后二维波数谱的支撑域的变化，可以用投影的原理来理解，如图1所示。通过(14)可以得到图2中的第一幅图，将第一幅图(即三维图)分别投影到KR-KX轴和KY-KX轴，可以发现，在KR-KX域是梯形支撑域，在KY-KX域是一个圆环，考虑到KY-KX有一定的取值范围，因此在KY-KX域是扇形环。那么就可以得到STOLT插值前后的支撑域的变化。

图1 波数谱支撑域的变化

STOLT插值的两个关键步骤是插值和数据的搬移，插值的目的是准确找出点的位置，搬移的目的是要进行方位向压缩、距离徙动校正和高阶误差的补偿。

假设数据已经插值完毕，数据的搬移可以用下面的图来表达

图2 数据搬移示意图

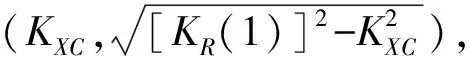
(15)

(16)

需要注意的是公式(16)中没有乘以斜距(R-Rs)·cosθ

在正侧视情况(即θ=0)下，(16)式的意义就更加明显，

(17)

观察(17)，可以发现，等号右边第二项为方位向调制函数，第三项为距离徙动，第四项为二次距离压缩项，第五项为三次误差函数。那么，很明显RMA算法通过搬移，在二维频域完成了方位向压缩、距离徙动校正、二次距离压缩、三次项误差的校正以及高阶误差的校正。从这里也可以理解为什么RMA算法是很精确的算法，它的精确性不只在于它补偿了高阶甚至无穷阶的误差，克服了二次距离压缩(SRC)算法、线性调频(CS)算法、非线性调频(NCS)算法等不同程度近似的问题，还在于它克服了SRC无法处理处理徙动沿距离向的空变形以及SRC算法和CS算法无法处理调频率距离向空变形的问题。但是，我们也不能否认插值的运算量是比较大的，所以尽管RMA算法是最优的，我们仍然需要研究SRC算法、CS算法、NCS算法等。

至于有斜视角的(16)式，可以与级数反转法作一对比，或许能更加深刻理解其含义，目前关于二者之间的关系有待进一步的研究，因为级数反转法虽然可以求得精度比较高的二维频谱，但是一般要泰勒展开到四阶，形式相当复杂，并不容易观察。

插值后，再进行二维IFFT可以得到聚焦图像。具体的算法流程图如图3所示。

图3 RMA算法流程图(非Dechirp)

3.2 Dechirp处理方法

需要注意的是在本部分也即Dechirp处理方法中所有的推导是在斜视角为0的情况下。因此斜距可以写为

(18)

Dechirp处理方法也比较简单，首先，接收的回波信号未去载频，为

(19)

首先构造参考函数，

(20)

Dechirp后的信号为

(21)

利用卷积公式，可以进一步将上式写为

sd=exp(-j·KR·(r(ta)-Rs))⊗

(22)

其中，

(23)

因此剩余视频相位的去除可以将回波信号IFFT变回到距离时域，乘以函数(24)，达到去除的目的，然后在距离向FFT，变回到波数域，进行二维匹配滤波，滤波函数为(25)。

(24)

(25)

基本的流程图如下图所示。

图4 RMA算法流程图(Dechirp)

4 仿真结果

4.1 非Dechirp仿真结果

根据上面的推导，我们进行仿真验证，非Dechirp处理方法的仿真参数列于表1。在图5中，我们仿真了三个点。为了进一步说明成像算法的有效性，我们对边缘处的点做了评估，如图6所示。观察图6可以发现，距离向和方位向的峰值旁瓣比达到了要求，二维等高线图也清晰可见，没有发生耦合现象。

表1 非Dechirp处理方法仿真参数

图5 点目标仿真结果

图6 目标3处评估结果

4.2 Dechirp仿真结果

对于Dechirp的方法，仿真参数列于表2中。同样为了观察STOLT插值的效果，我们给出了中心点处的插值前后的效果图如图8和图9所示。为了说明算法的有效性，我们对中心点处和(50 m,50 m)处的目标进行了仿真，仿真结果分别如图7和图11所示，它们的评估结果如图10和图12所示。同样观察图10和图12，我们可以知道评估结果接近理论值，证明了算法的有效性。

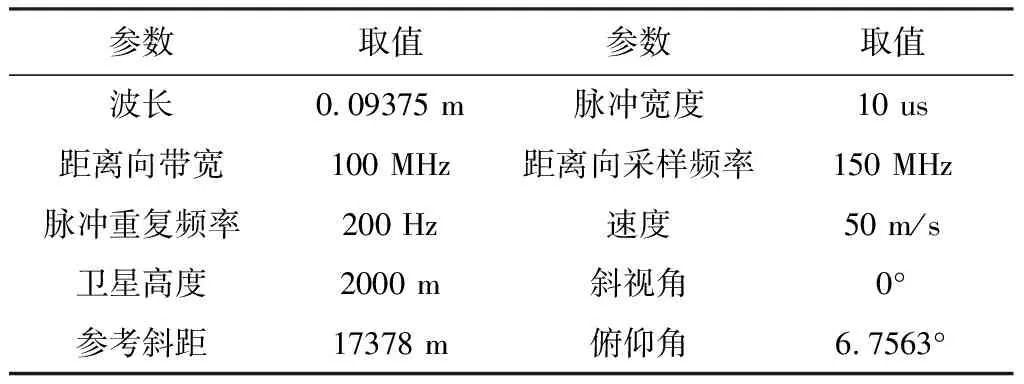
表2 Dechirp处理方法仿真参数

图7 中心点仿真结果

图8 中心点STOLT插值前图

图9 中心点STOLT插值后图

图10 中心点评估结果

图11 (50，50)处仿真结果

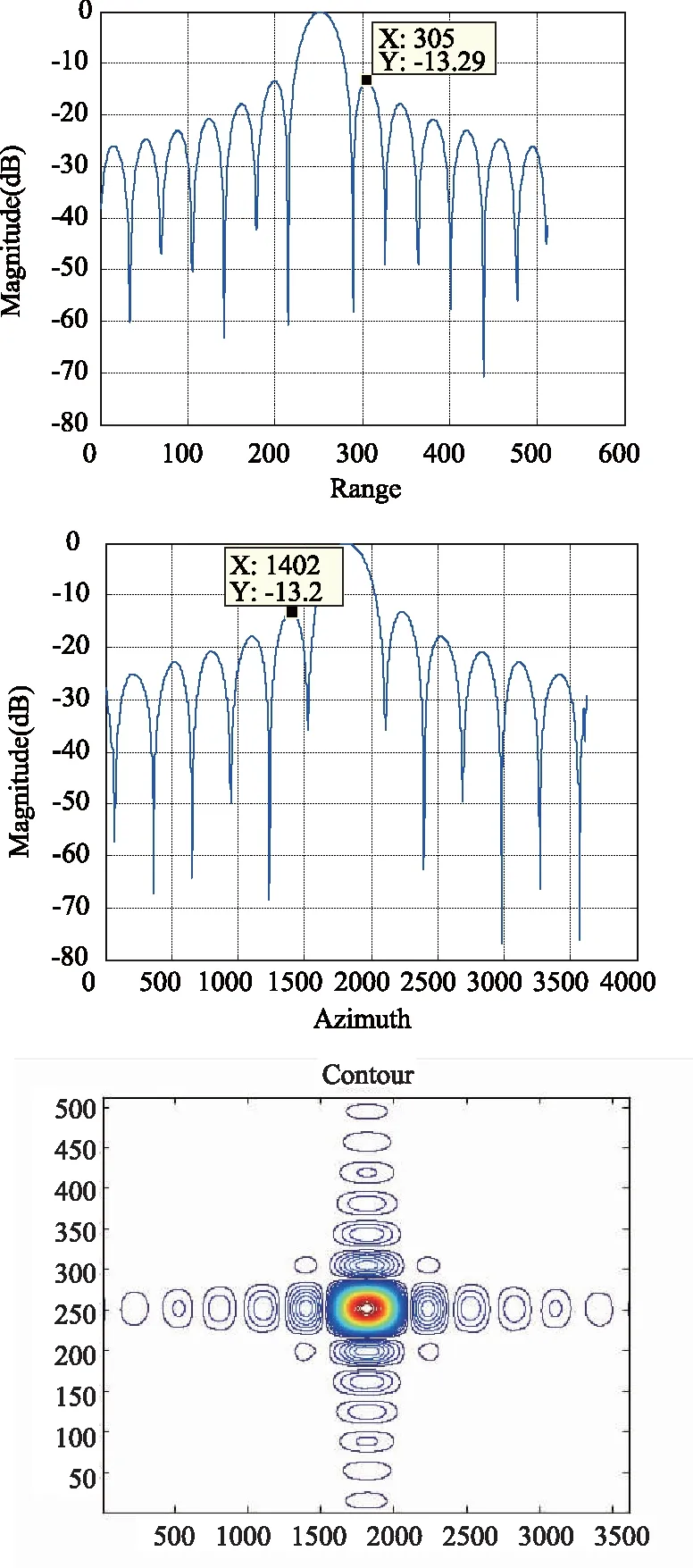
图12 (50，50)处评估结果

5 结 语

RMA算法作为一种最优的SAR成像算法，一直受到人们的青睐。本文主要研究了RMA算法，并给出了成像结果。首先本文给出了在合成孔径雷达领域的三种斜距的基本写法，并给出了各自通常的适用邻域；然后本文主要推导了信号的波数谱表达式；在成像算法的推导中，本文给出了两种情况下的RMA算法，并详细解释了STOLT插值的原理，而且通过分析，可以理解为什么RMA算法是最优的成像算法；在仿真中，本文同样给出了两种形式下的RMA成像算法结果，仿真结果也证明了其有效性。