杂波干扰下雷达微弱多目标检测跟踪方法

宋 强

(辽东学院机械电子工程学院,辽宁 丹东 118003)

0 引 言

现代雷达的基本功能是目标的跟踪和检测，隐身技术被广泛的应用到军事武器装备的研究中，如巡洋舰、战斗机、坦克、导弹和轰炸机等，雷达回波信号的强度受雷达散射截面积的影响[1-2]。微弱目标的检测会受到多种因素的影响，如干扰、杂波、噪声和强目标掩盖等[3]。在微弱目标的跟踪和检测过程中，远距离目标的回波信噪比较低、且强度较弱，微弱目标容易被杂波淹没，对微弱多目标的检测造成影响，在杂波干扰下对雷达微弱多目标进行检测是当代社会亟待解决的问题[4]。当前雷达微弱多目标检测方法存在信噪比低和检测结果准确率低的问题，需要对雷达微弱多目标检测方法进行研究[5]。

许述文等[6]提出了一种基于四极化通道融合的微弱多目标检测方法，该方法对四个极化通道的频域特征和时域特征进行提取，得到微弱目标的向量熵、相对多普勒峰高和平均振幅，并在极化通道维度上完成频域特征和时域特征的融合，根据融合结果得到四极化通道融合特征，采用快速凸包学习算法在三维特征空间中确定杂波的判决区域，完成微弱多目标的检测，该方法不能有效的去除目标回波中存在的噪声，信噪比较低。邓亚琦等[7]提出了一种机载外辐射源雷达微弱多目标检测方法，该方法通过构建微弱多目标信号和杂波模型，对信号进行滤波处理，在Keystone变换的基础上完成信号相对径向速度距离的校正，完成杂波干扰下雷达微弱多目标的检测，该方法检测得到的目标运动轨迹与实际轨迹不符，检测结果的准确率较低。陈洪猛等[8]提出了一种基于时域降维的雷达微弱多目标检测方法，该方法对多帧数据和单帧数据进行滤波处理，去除数据中的杂波，对处理后的数据进行平滑和降维，最后对信号进行Radon变化，完成雷达微弱多目标在杂波干扰下的检测，该方法的抗干扰能力弱，得到的目标回波信号信噪比低。

为了有效去除目标回波信号中存在的噪声信号，和得到的较准确的目标运动轨迹，提出一种杂波干扰下雷达微弱多目标检测方法，所提方法可以被证明具有较强的抗干扰能力和较好的轨迹跟踪性能。

1 信号模型

设L(t)代表的t时刻的基线距离，在t=0处L(t)的泰勒展开式如下：

L(t)≈Rd+vdt+adt2/2

(1)

式中，Rd=L0；vd=-vrcosα代表的是径向的直达波速度；ad=(vrsinα)2/L0代表的是径向直达波的加速度。

设ΔRci2(t)、ΔRci1(t)分别代表的是相对于径向直达波的，距离天线2和天线1杂波散射点的回波，其计算公式为：

Rci1(t)≈Rci+vcit+acit2/2

(2)

ΔRci2(t)≈ΔRci1(t-Δt)-φ(t-Δt)

(3)

式中，参数Δt=d/vr；参数φ(t)=[vdΔt+ad(Δt)2/2]+adtΔt；aci、vci和Rci分别代表的是天线1接收的第i个杂波散射点回波的径向相对加速度、径向相对速度和初始相对距离。

设s(t)代表的是发射源的基带信号，ykc(t)代表的是第k个通道的杂波信号，其计算公式为：

(4)

式中，Aci代表的是信号的相对复幅度；fc代表的是载波频率；c代表的是光速；其中参数τ1=0；φ1(t)=0；τ2=Δt；φ2(t)=-φ(t-Δt)。

设ykt(t)代表的是第k个通道的微弱目标回波信号，其中k=1,2。同理得到ykt(t)的计算公式为：

(5)

式中，j为常数；Aktl代表的是第l个微弱目标散射点回波在两个通道内的相对复幅度；ΔRtl1(t)代表的是直达波与微弱目标散射点回波之间的径向距离，ΔRtl1(t)≈Rtl+vtlt+atlt2/2；atl、vtl、Rtl分别代表的是天线1接收微弱目标回波的径向相对加速度、径向相对速度和初始相对距离。

设yk(t)代表的是第k个通道中的回波信号，通过公式(4)和公式(5)得到回波信号yk(t)的表达式：

yk(t)=ykt(t)+ykc(t)-nk(t)

(6)

式中，nk(t)代表的是通道内存在的噪声信号。

2 雷达微弱多目标检测方法

在检测雷达微弱多目标之前，需要对目标回波进行离散化处理，得到期望输出和实际输出之间存在的误差，通过正则方程得到滤波器的实际输出信号，去除回波信号中存在的强目标回波和噪声，重构信号，得到微弱目标的回波信号[11]。对回波信号做相参处理，建立距离-方位二维序列，采用两级门限检测方法[12]得到微弱目标的状态序列，通过逆序递推法得到雷达微弱目标的运动轨迹，完成杂波干扰下微弱多目标的检测。

设T1代表的是回波信号中存在的强目标，I-1代表的是强目标T1周围存在的弱目标，对目标回波信号yk(t)做离散化处理，得到离散后的目标回波x(n)，其表达式为：

(7)

式中，n代表的是采样的时间；A1s1(n)为强目标在通道内的回波；Aisi(n)为第i个弱目标在通道内的回波。强目标回波和弱目标回波存在差异，并且存在频率偏移和时间延迟。

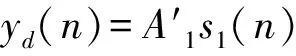
e(n)=yd(n)-x(n)·h(n)

(8)

通过公式(8)得到能量误差‖e(n)‖2，计算公式如下：

(9)

公式(10)为正则方程，通过正则方程对最小二乘滤波器进行求解：

(10)

对公式(10)进行简化：

Rh=q

(11)

(12)

(13)

得到残留项rem(n)和yd(n)的互相关Rrem_yd(n)：

(14)

通过公式(14)得到滤波处理后的目标回波A1，完成目标回波信号的重构：

(15)

对回波信号A1做相参处理，提取相参区间中幅值最大的序列作为回波序列，建立距离-方位二维序列。设th1代表的是第一级低门限，通过th1删除序列中存在的弱小点，并对其进行K次扫描，构成方位-距离-时间序列Z(k)={zij(k)}，其中1≤i≤M，1≤j≤N，1≤k≤K。

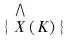
(16)

其中，最终门限th2的计算公式为：

th2=-bnln[-ln(1-an)]

(17)

参数an和bn的计算公式如下：

an=μ+σ[2lgn1/2-(lglgn+lg4π/4lgn1/2)]

(18)

bn=2lgn1/2/σ

(19)

n=M·N·V2

(20)

式中，μ代表的是价值函数在微弱目标轨迹累积K帧时的均值；σ代表的是价值函数在微弱目标轨迹累积K帧时的方差；M代表的是距离单元；N代表的是方位单元数；V代表的是方位向和距离向的速度单元数。

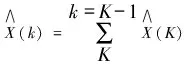
(21)

3 实验结果与分析

为了验证杂波干扰下雷达微弱多目标检测方法的整体有效性，尤其是纯方位的目标跟踪检测，因此抗干扰能力十分重要，一般可以采用去噪后的信号频率作为度量标准。本次测试的平台为Intel双核酷睿i5, 主频2.92 GHz，8 GB RAM的个人台式电脑，采用MATLAB2011b编程测试。参数采用默认参数设置。分别采用杂波干扰下雷达微弱多目标检测方法(方法1)、基于四极化通道融合的微弱多目标检测方法(方法2)、基于时域降维的雷达微弱多目标检测方法(方法3)进行测试，对比三种不同方法的抗干扰性能，测试结果如图1所示。

图1 三种不同方法的去噪结果

分析图1(a)可知，与去噪前的信号频率曲线相比，采用杂波干扰下雷达微弱多目标检测方法得到的去噪后的信号频率曲线较为平缓。分析图1(b)和图1(c)可知，与去噪前的信号频率曲线相比，采用基于四极化通道融合的微弱多目标检测方法、基于时域降维的雷达微弱多目标检测方法得到的去噪后的信号频率曲线抖动较大。对比图1(a)、图1(b)和图1(c)可知，采用杂波干扰下雷达微弱多目标检测方法对目标回波信号去噪后，得到的信号频率曲线较为平缓。证明杂波干扰下雷达微弱多目标检测方法可有效的去除目标回波信号中存在的噪声，去噪效果好，抗干扰能力强，去噪后的目标回波信号信噪比较高。

分别采用杂波干扰下雷达微弱多目标检测方法(方法1)、基于四极化通道融合的微弱多目标检测方法(方法2)、基于时域降维的雷达微弱多目标检测方法(方法3)进行测试，对比三种不同方法检测得到的目标运动轨迹，并将检测得到的运动轨迹与实际轨迹进行对比，对比结果如图2所示。

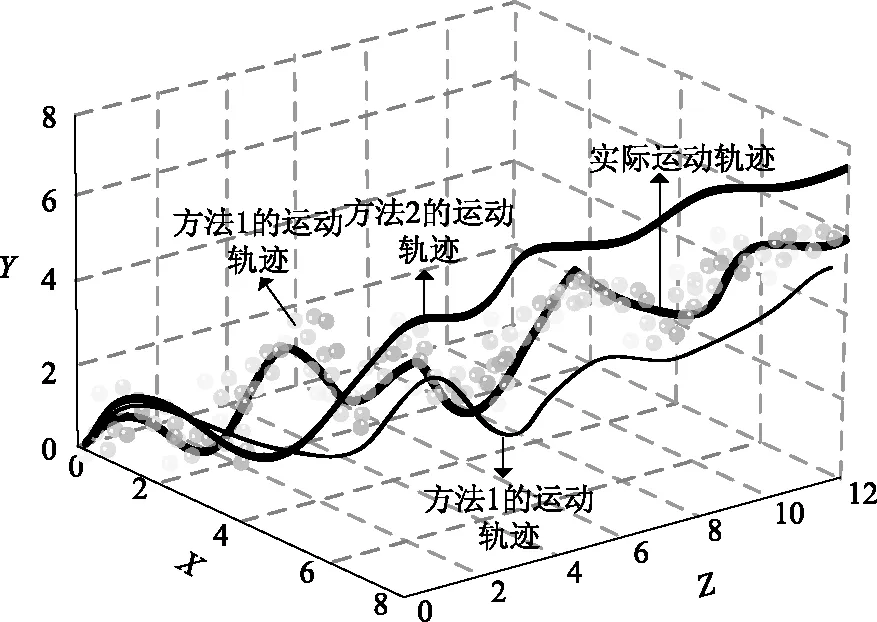
图2 三种不同方法的运动轨迹

分析图2可知，采用杂波干扰下雷达微弱多目标检测方法检测得到的微弱目标运动轨迹与微弱目标实际运动轨迹相符；采用基于四极化通道融合的微弱多目标检测方法、基于时域降维的雷达微弱多目标检测方法得到的微弱目标运动轨迹与微弱目标实际运动轨迹相比误差较大。因为杂波干扰下雷达微弱多目标检测方法对回波信号做相参处理，采用两级门限检测方法得到微弱目标的状态序列，根据状态序列对目标进行定位，得到目标的运动轨迹，提高了杂波干扰下雷达微弱多目标检测方法的检测结果准确率。

4 结 语

在杂波干扰下，雷达接收的微弱运动目标回波信号的信噪比和强度较低。当前雷达微弱多目标检测方法存在抗干扰能力差和检测准确率低的问题。提出一种杂波干扰下雷达微弱多目标检测方法，解决了当前方法中存在的问题，可有效的去除目标回波信号中存在的噪声信号，得到的微弱多目标的运动轨迹准确率高，促进了雷达技术的发展。