电子网络环境下故障数据粒子群融合搜索算法

2018-11-26宋定宇

中国电子科学研究院学报 2018年5期

宋定宇

(南阳理工学院,河南南阳 473000)

0 引言

由于电子网络会出现的各种问题，需要通过网络运维人员对此排查，准确定位并给予解决[1-2]。许多电网方向的研究学者对电子网络故障的研究取得了十分显著的成果，朱蓉等[3]人提出了一种基于融合优质粒子分布的粒子群优化算法，但其未设计加速因子，算法收敛速度慢。文献[4]提出的粒子群运动特性下的神经网络目标搜索算法，其主要缺点是粒子群极易停滞在局部极值点。文献[5]针对现有粒子群人工神经网络存在误差大、不易收敛等问题，在粒子群动态运动特性的基础上，提出了一种神经网络目标搜索算法，通过方向因子对传统的粒子群算法进行了改进。提出了早熟判断机制，以保证收敛效果，文献[6]与之相似。

为了提升电子网络故障数据的搜索效率和故障诊断率，本文提出电子网络环境下故障数据粒子群融合搜索算法，在改进PSO算法中设计加速因子，使得每个粒子快速集合到局部最优解，以提高收敛速度。将模式搜索法与改进PSO算法相融合，引导粒子群搜索最优位置。

1 电子网络环境下故障数据粒子群融合搜索算法

1.1 基于PSO的故障诊断方法

1.1.1 基本PSO算法

粒子群优化(Particle Swarm Optimization，PSO)算法是具有随机性的优化算法，初始时是一群随机粒子(随机待选解)，经过数次迭代获得最优解[5]。在反复迭代过程中，粒子群的更新与迭代过程中的两个最值有关。其一是粒子本身获得最值，这是粒子极限最值；其二是在搜索群组最值，也就是群组最值(或粒子群区域最值)[6]。当获得粒子极限最值和群组最值时，粒子的自身更新速度与行动轨迹公式为：

wij(u+1)=awij(u)+φ1j(u)[zij(u)-kij(u)]+

(1)

kij(u+1)=kij(u)+wij(u+1)

(2)

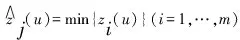
1.1.2 改进的带扰动项PSO算法

通过在反复实验后验证公式(1)，其结果在既定范围内的群组最值基本恒定，上下浮动不大，由公式(1)中αwij(u)确定粒子实时位置，同时推测出粒子群的运动同向，持续运动到区域极限位置[7]，粒子运动速度下降直至运动停止，此时粒子处于区域极限位置，为了防止这种情况出现，对PSO算法进行优化，在反复实验时增加速度进化因子L。

在求解最小值时，令L为上次迭代的全局最优解为目前迭代的全局最优解，即：

(3)

式中，g(·)为合适度函数，通常L≥1，L越大代表进化速度越快[8]。反复进行迭代实验，搜索次数增大，若L一直等于1不无法获得最佳解，此时，应用PSO算法的粒子处于区域极限位置，是全局最值。根据以往的研究经验，若L小于◁(◁∈[3,6])，粒子很可能正处于区域极限位置，即全局最值，为了避免这种情况，应该改变粒子的初始位置，用来辅助实验的进行，更新后重新确定粒子位置继续搜索，从而提升整个粒子群在电子网络下的故障检测能力[9]。

改进PSO算法每次迭代时都计算粒子的进化速度，当L小于◁时，在速度更新方程中引入负扰动项，用来改变粒子的运动方向，此时式(1)变为：

(4)

借鉴文献[11]的基本PSO收敛性研究结果，使得带扰动项的PSO改进算法粒子群最终收敛于某平衡点，则有：

(5)

1.1.3 加速因子设计

在对算法进行优化的过中，需要分为很多阶段，在初始阶段，我们需要重点关注粒子本身的运动轨迹，以免产生所有粒子都集中到区域极限位置；在最终阶段，应该关注最优粒子的轨迹，增大收敛速度[12]。故此，对于优化算法的整个阶段，d1应逐渐减小，d2应逐渐增大。优化后计算加速因子公式如下：

(6)

(7)

式中，d1min、d1max、d2min、d2max代表加速因子取值范围；迭代次数为1时，d1≈d1max，d2≈d2max；当迭代次数达到最大时，d1=d1max，d2=d2max，同时d1与d2呈幂函数形式非线性变化[13]。

1.2 初始步长可伸缩的模式搜索法

1.2.1 模式搜索法

Hooke等人在1964年提出了模式搜索算法，模式搜索算法无需求导，适用于复杂函数的优化中，能够为我们提供技术支撑[14]。因此将模式搜索法和改进的PSO算法相结合，实现电子网络环境下的故障数据搜索[15]。模式搜索法具体步骤如下：

(1)初始化：通过迭代计算，获得最佳解，然后将这个最佳解作为初始迭代点。

设定初始步长ζ>0，速度因子θ≥0，步长递减参数0<σ<1，精度参数ρ>0，搜索变量q1=z，循环次数s=1；

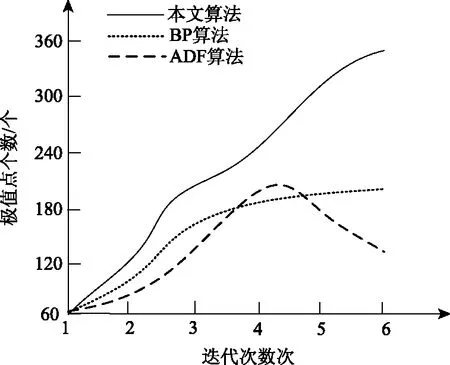
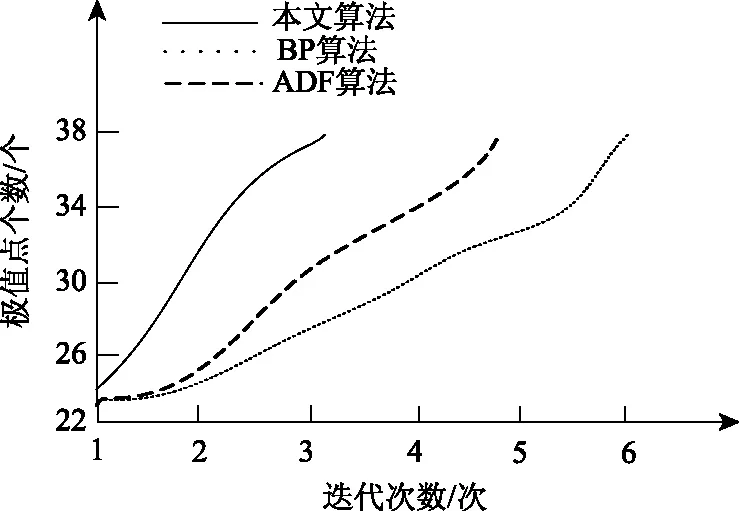
(2)搜索移动：维数i=1,2,3,…,E，若f(qi+ζei)

(3)模式移动：若f(qE+1)

(4)停止判断：如果ζ<ρ，那么{kbest=k(s),输出kbest，停止运算}；否则{减少步长ζ=σζ，转(2)}。

1.2.2 初始步长可伸缩的模式搜索法

模式搜索法主要解决的问题。第一，为解决对起始位置十分敏感这一问题，通过迭代计算，获得最佳解，然后将这个最佳解作为初始位置；第二，为解决计算量过于庞大这一问题，提出一种初始步长伸缩算法。对于当前模式的迭代次数count，令count=s，即反复搜索s次，其获得结果没有改变。对于模式搜索法中的初始步长i来说，当i减小时，初始点变小，s减小计算次数减少，从而减小了计算次数，增加了计算效率。为了防止粒子恰好位于区域极位置，当搜索次数s>3时，将初始步长增大，扩大搜索范围。

通过以上步骤，能够减少电子网络环境下故障数据搜索的计算量。初始步长ζ的生成过程如下所示：

ζorigin=0.3×zmax；

If(count==1‖(s>4)){s=0;ζ=ζorigin;}

Else{ζ=ζ/12(count-1);}

End

2 实验分析

本文所用实验平台是Intel酷睿双核i3处理器，主频2.12 GHz，4 GB RAM的个人笔记本电脑，采用matlab和C混合编程。对于文中的数据粒子群融合搜索算法，为验证其各方面表现，采用三个对比实验进行验证。

实验相关参数设置如下：

λmax=0.8，λmin=0.5，φ=0.2，m=3，d1min=1.37，d1max=2.64，d2min=0.6，d2max=2.38，停滞阈值threshold=12。

模式搜索参数设置如下：

初始步长ζ=0.3zmax，速度因子θ=2，步长递减参数σ=0.8，精度参数ρ=11-6。

2.1 与同类算法结果的对比和分析

实验将本文算法与融合优质粒子分布的粒子群优化算法(算法1)和粒子群运动特性下的神经网络目标搜索算法(算法2)进行比较，两个对比算法均为粒子群算法，算法参数设置相似，实验所用算法和本文算法的条件相同，因此对照实验具有可信性。

算法1运用10个测试函数，算法2运用5个测试函数。实验比较三个算法共用的测试函数最优值的均值。算法1的种群规模是35，维数是35；算法2的分别是25和30；本文算法的种群规模是25，维数是30。算法1的迭代次数范围是105-2×105，算法2则为1500，本文算法仅为150，对比结果如表1所示。

表1 三个算法测试结果对比

由表1可知，算法1在Gosenbrock和Destigom两个函数上收敛到了已知最优解0，本文算法在Lcheak、Gosenbrock和Destigom三个函数上收敛到了已知最优解0，同时本文算法在其他函数上更加接近已知最优解。另外，本文算法的迭代次数也远远少于另外两个算法，与算法2相比，针对其中4个函数，本文算法在解的精度上更优。

2.2 误差分析

实验应用采用神经网络方式对电子网络环境下的故障建立学习算法模型。神经网络由三部分构成，分别是输入层、输出层、隐含层，输入与输出部分都分为12个单元，因此需要拥有与之对应的故障模式向量和二值故障编码。在故障检测过程中对隐含单元进行检测，将初始节点数设置为15，采用300组样本完成训练，同时采用相应的故障向量与二值故障编码。本文算法的主要参数为：d1=d2=2.5；amax=0.90；amin=0.03；ed=0.4；◁=4；最大迭代次数为3000；粒子数量为50。训练结束后故障向量和编码的对应关系储存在电子网络中。

在实验中引入反向传播(Back Propagation, BP)算法和自动方位搜寻器(Automatic Direction Finder,ADF)算法，在相同的电子网络中建立故障对应关系，与文中算法比对。这两个算法的最大迭代次数为5000，运用TRAINBP函数训练网络。三种算法的误差曲线如图1所示。

图1 三种算法的误差曲线

本文算法在电子网络环境下的训练误差在1450次迭代后达到0.15，而BP算法的训练误差在5000次迭代后达到1.85，ADF算法的训练误差在5000次迭代后达到0.95。由此可见，本文算法的误差显著低于其他两种算法，能够满足电子网络环境下故障诊断实时性的要求。

2.3 收敛速度分析

为验证本文算法的收敛速度，以BP算法和ADF算法作为对比，图2 为三个算法在迭代过程中搜索到极值点的个数。

图2 三种算法迭代过程中搜索到极值点个数

由图2可知，本文算法在迭代后期依旧能够搜索到较多的极值点，当迭代次数为6时，搜索到的极值点个数为340，搜索并未停止，这说明本文算法具有较强的全局搜索能力。而另外两个算法在迭代次数为6时搜索到的极值个数分别为140、190，明显低于本文算法。因此，本文算法在相同迭代次数的条件下，能够搜索更多极值点，具有较高的搜索性能。

图3为三个算法收敛速度对比，由该图可以看出，本文算法在第3次迭代时即搜索到全部极值点，而另外两个算法分别在第4.5次和第6次迭代时搜索到全部极值点。