淮河干流与洪河洪水遭遇规律研究
2018-11-24瞿思敏赵梦杰牟时宇董丰成
冯 颖 石 朋,2 王 凯 瞿思敏 赵梦杰 牟时宇 董丰成 陈 琛
(1. 河海大学 水文水资源学院, 南京 210098; 2. 水文水资源与水利工程科学国家重点实验室, 南京 210098; 3. 淮河水利委员会水文局 信息中心, 安徽 蚌埠 233001)
淮河流域地处我国南北气候过渡地带,气候条件复杂,支流多为扇形网状,使洪水集流迅速、洪水灾害频繁.洪河口(洪河入淮口)以上为上游,落差178 m,占淮河总落差的89%,因此上游段干流水势湍急,是防洪重点.洪河为淮北山丘河流,全长455 km,流域面积为12 303 km2,支流汝河的汇入加大了河流径流量,而王家坝站位于淮河与洪河的交汇处下游,一旦淮河上游洪水遭遇到洪河洪水,将使王家坝站的防洪形势更为险峻.因此淮河干流与洪河的遭遇分析对流域的防洪具有重要意义,选取淮滨站为淮河上游干流控制站,班台站为洪河控制站,以两站1959~2014年实测的日流量资料分析淮河干流与洪河的遭遇规律(图1展示了研究区域内的水系图及洪水传播时间).
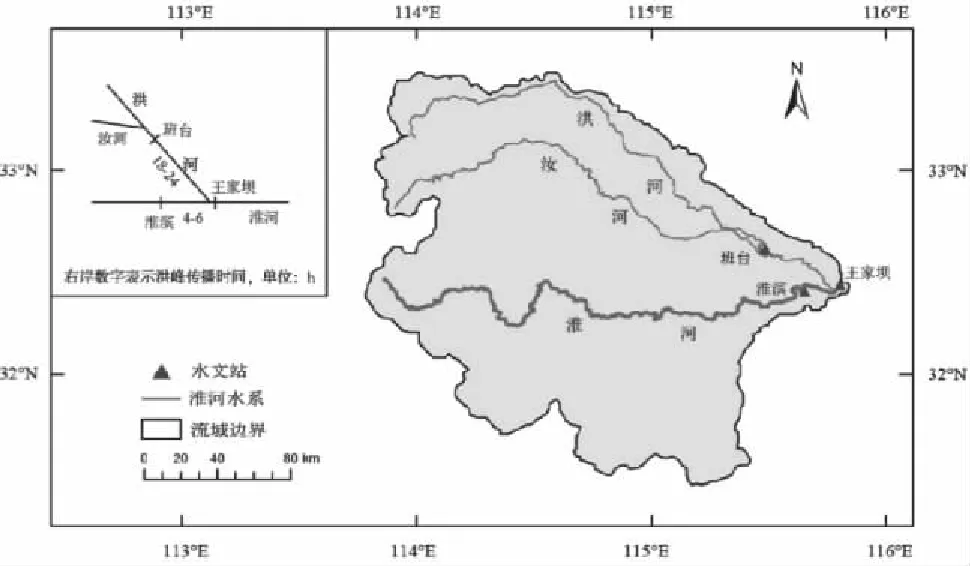
图1 研究区域和水文站位置
现普遍认为洪水遭遇问题实质上是多变量的频率组合问题,因此可采用多变量分析方法进行研究,近年来Copula函数在水文上的应用[1]为设计洪水的遭遇研究提供了新思路,张新田等[2]通过Copula函数构造了金沙江干流与雅砻江洪水年最大洪峰流量联合分布研究两江遭遇规律,但边缘分布仍采用一致性洪水频率分析方法.然而,受到气候变化和人类活动的影响,水文序列不都具有一致性特征.现有的洪水遭遇研究均未考虑洪水遭遇概率随时间的变化.本文引入具有时变性的GAMLSS模型[3-4]拟合量级分布,以Von Mises分布拟合洪水发生时间,并通过Copula函数构造时间及量级的联合分布,分析两河洪水发生时间和发生量级的遭遇规律.
1 洪水发生时间的遭遇分析
1.1 Copula函数
Copula函数是定义在[0,1]上的多维联合分布函数,其构造方式灵活,不受边缘分布限制,对于二维联合分布,可表述如下:
F(x,y)=Cθ(F(x),F(y))=Cθ(u,v) (1)
其中,Cθ(*)表示Copula函数,F(x),F(y)表示随机变量X,Y的边缘分布.Copula函数种类众多,其中Archimedean Copula函数结构简单且可以构造形式多样、适应性较强的多变量联合分布函数,在水文领域中应用广泛,因此本文采用此类函数族.该族函数中又包含了Gumbel-Hougaard Copula(GH Copula)、Clayton Copula和Frank Copula等函数形式,函数形式的选取步骤为:首先根据两变量的正负相关性及尾部相关性拟选Copula函数形式并用拟牛顿估计法来估计各种函数的参数;接着以AIC最小准则、RMSE最小准则及尾部相关系数最接近为标准进行择优[5].
1.2 时间边缘分布及洪水遭遇的时间特征
将洪水发生时间转换为弧度制矢量x,x=2πDj/L,其中,Dj表示洪水发生在汛期第j天,L为汛期总长度.采用混和Von Mises分布拟合,其概率密度函数为:
0≤x≤2π,0≤ui≤2π,ki≥0 (2)
其中,ui和ki分别为各组成成分的位置参数和尺度参数,pi表示混和比例,I0(ki)为0阶Bessel函数.
由于年最大日流量发生时间基本在汛期,因此采用1959~2014年共56年的实测日流量资料,统计每年5~9月年最大日流量及相应时间,并统计发生时间在每个时段(按旬分)的频率,拟合的Von Mises函数参数结果见表1.

表1 混合Von Mises参数估计结果
两站拟合效果如图2所示,两河洪水发生时间集中于7~8月份,具有正相关性,择优后采用GH Copula进行拟合,参数估计结果θ为2.1.
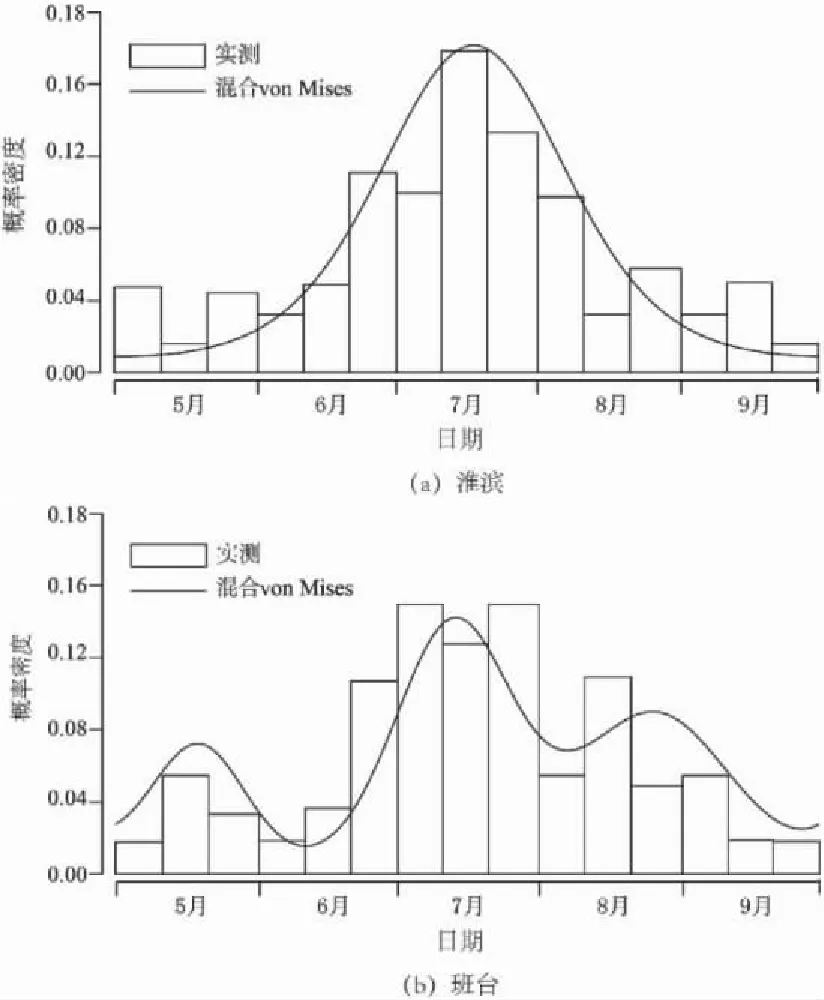
图2 淮滨站与班台站年最大日流量发生时间概率密度拟合图
考虑洪水历时,本文将洪水时间遭遇定义为年最大日流量发生时间相差4 d以内,因此两河年最大日流量发生时间在第i天遭遇的风险率为:
pi=p
(ti≤Th≤ti+1,ti+τhb-Δt≤Tb≤ti+τhb+Δt) (3)
其中,ti表示汛期第i天,Δt表示两河洪水发生时间间隔,τhb表示两站至交汇处的传播时间差(淮滨站与班台站传播时间差为16 h).
图3绘制了两河年最大日流量在汛期每天的遭遇概率,其中淮河干流与洪河6月份之前及9月份之后遭遇可能性很小,不足0.05%,两河最易在7~8月份遭遇,遭遇概率均在0.10%以上,且7月14日遭遇概率最大,达到0.34%.因此在7~8月份应充分考虑淮滨站与班台站之间的预泄错峰调度.
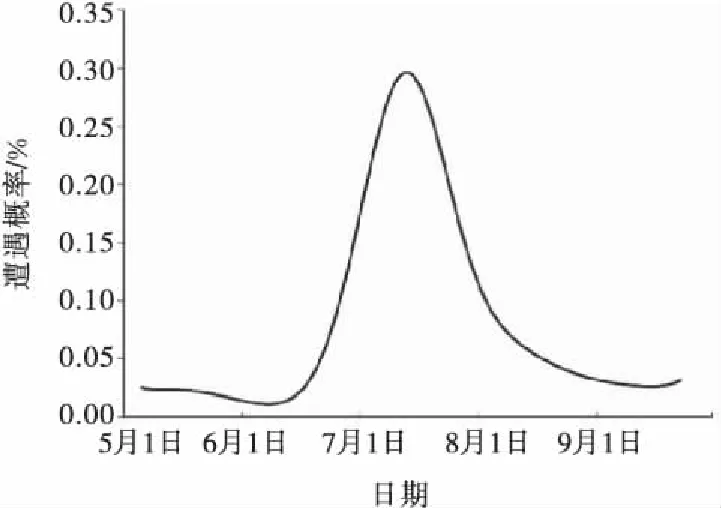
图3 淮河与洪河遭遇风险图
2 洪水量级遭遇规律分析
由于气候变化、人类活动的影响,水文序列非一致性特征日益明显,因此采用Mann-Kendall检验法[6]对淮滨及班台的实测最大日流量序列进行趋势性分析,见表2.

表2 两站点最大日流量Mann-Kendall趋势分析
结果表明,淮滨站年最大日流量存在下降趋势,班台站具有上升趋势,因此采用GAMLSS模型进行拟合更符合实际情况.
2.1 洪水量级边缘分布
GAMLSS模型是由Rigby等[3]提出的结合广义线性模型及广义可加模型的一种半参数回归模型.模型认为同一个时间序列y1,y2,…,yn相互独立且服从同一分布函数Fy(yi|θi),其中θi为参数(位置参数,形状参数和尺度参数)组成的向量,其方程为:
(4)
其中,θk和ηk是长度为n的向量,βk是长度为Jk的参数向量,Xk是n×Jk的解释变量矩阵,Zjk是已知的n×qjk固定矩阵,γjk为服从正态分布的随机变量.本文不考虑随机效应对分布参数的影响,选择4种极值分布函数分析:Gumbel(GU)、Gamma(GA)、Lognormal(LOGNO)和Weibull(WEI).
根据GD、GAIC、SBC最小准则选择合适的GAMLSS模型,具体见文献[3],结果表明,两站GAMLSS模型中极值分布函数均选择WEI分布,淮滨站均值与方差均有非一致性,班台站方差具有非一致性,均值为常数,拟合结果见表3.

表3 淮滨站与班台站量级边缘分布参数拟合结果
选取残差均值、残差方差、Filliben系数以及K-S检验作为定量评价指标,见表4.两站的GAMLSS模型均通过显著性水平为0.05的假设,因此认为所选的模型合理.
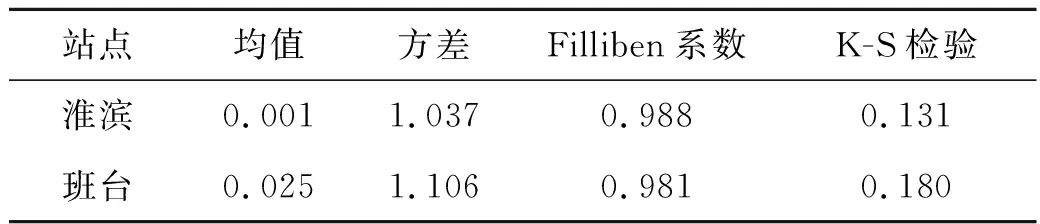
表4 两站的GAMLSS模型残差定量评价指标
注:在显著性水平为0.05时,Filliben系数为0.978[8]与K-S检验为0.182为临界值,当Filliben系数大于0.978与K-S系数小于0.182则认为模型通过检验.
残差图的分布趋势是判别模型拟合效果的重要定性指标[7].从如图4所示Worm图中可以看出所有点据均落在95%的置信区间内(即上下两条灰色虚线),且QQ图中所有的点据基本沿着45°直线分布,说明所选的模型实际残差与理论残差具有非常好的相关性.
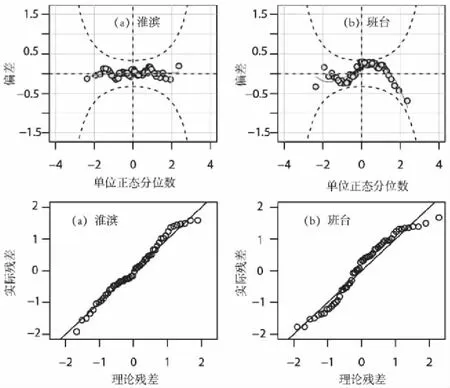
图4 两站GAMLSS模型的拟合残差检测图及线性回归正态QQ图
2.2 洪水量级遭遇规律分析
2.2.1 量级联合分布
两站年最大日流量具有正相关性,而GH Copula具有正相关性及上尾相关性,适合描述洪水极值事件,参数估计采用拟牛顿估计法得到参数θ=1.865.
图5给出了经验频率与理论频率的拟合图,左图中理论频率(折线)与实际频率(点据)基本重合,且QQ图中点据基本沿着45°直线分布,表明该联合分布拟合结果较好.
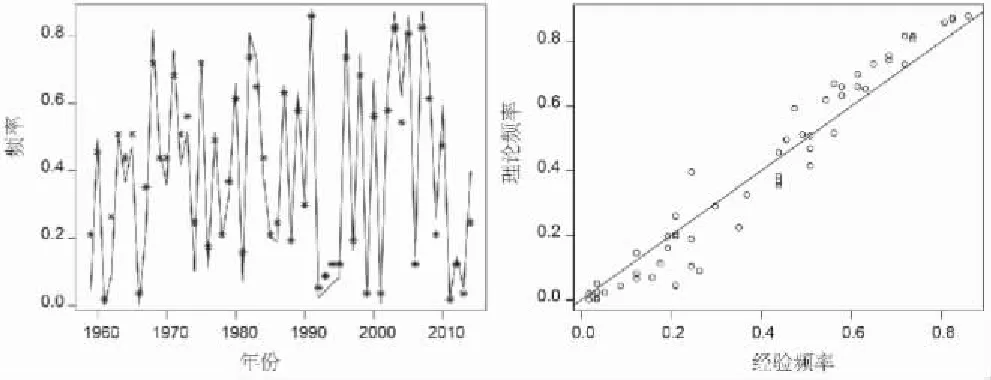
图5 淮滨与班台年最大日流量联合分布理论估计与经验估计拟合效果图及QQ关系图
2.2.2 遭遇概率的时变性分析
遭遇概率定义为两站同时发生大于某一特定值的洪水(设计流量)时的概率,公式见式(5).
P(X>x,Y>y)=1-P(X≤xorY≤y)=
1-u-v+C(u,v) (5)
当u=v时表示同频率遭遇组合,是遭遇组合中具有一定代表性的组合形式.
图6展示了同一遭遇频率下的所有的遭遇组合形式,图6(a)为20%遭遇频率,图6(b)为10%遭遇频率,黑色虚线为P-Ⅲ分布函数计算所得等值线.
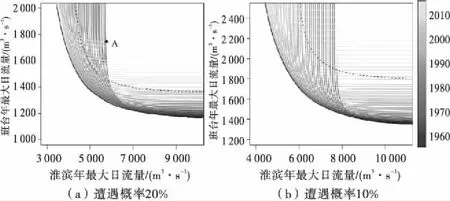
图6 遭遇概率等值线图
遭遇规律分析如下:
1)同一遭遇概率,随年份增加,等值线均向左上方移动,即同一遭遇频率,随年份增加遭遇组合形式逐渐向淮滨站流量减少而班台站增加的趋势转变;以P-Ⅲ分布函数计算所得遭遇等值线以上区域为风险区容易忽视由于气候变化而产生的可能遭遇组合(黑色实线与黑色虚线之间的组合形式),因此提出以多年遭遇概率等值线包络线(图中黑色实线)为界限划分风险区,充分考虑了气候因素引起的不确定性,较传统方法更为安全.
2)同一遭遇概率,遭遇概率等值线向上逐渐变稀疏而往左逐渐密集,说明随年份增加,洪水遭遇组合中班台站流量的变化越显著而淮滨站的变化幅度相对平缓,即受到气候环境的影响较小,以同频率组合为例,20%遭遇概率下,淮滨流量由6 736 m3/s减少为3 318 m3/s,减少了50.7%,而班台站由1 256 m3/s增加至2 210 m3/s,增加了76%,变化幅度大于淮滨站.
3)对于不同遭遇概率,10%的等值线较20%等值线更为稀疏,表明洪水遭遇概率越低其变化趋势就越显著,仍以同频率组合为例,在10%遭遇概率下,淮滨站流量由8 766 m3/s减少至4 049 m3/s,减少了53.8%,比20%遭遇概率淮滨的变化幅度大3.1%,而班台站增加了129%,比20%遭遇概率的班台流量变化幅度大53%,说明若仍采用传统的单一等值线,在估计小概率洪水遭遇组合中容易造成较大误差,尤其容易低估班台站流量,对防洪安全较为不利.
2.2.3 最可能组合
若下游站点的某一安全流量为zp,现假设上游两站流量分别为x,y,且满足zp=x+y,则组合形式有多种,最可能组合即在满足该等式条件下的概率密度函数f(x,y)的最大值:
f(x,y)=f(x,zp-x)=
c(FX(x),FY(zp-x))fX(x)fY(zp-x) (6)
考虑到王家坝警戒水位为27.5 m,王家坝闸的进闸流量为1 626 m3/s,现假设淮河与洪河发生洪水遭遇,控制两河年最大日流量组合值为5 000 m3/s.在该条件限制下,研究最可能组合情况随时间的变化趋势,为上游的防洪调度提供一定的依据.绘制出56年的可能遭遇情况,各曲线顶点处即每年的最可能遭遇情况如图7所示,结果表明:
1)由图7(a)知,随着年份的增加,最可能组合的风险率随年份的增加逐渐减少,且最可能组合呈现淮滨站的年最大日流量逐渐减少,班台站逐渐增加的趋势.如1959年的最可能组合为淮滨站流量4 010 m3/s且班台站流量990 m3/s,而2014年最可能组合为淮滨站流量3 400 m3/s,相应班台站流量1 600 m3/s.即在最可能组合中淮滨流量所占比例由80.2%减少为68.0%,而班台站流量相应地由19.8%增加至32.0%,该结果表明在未来防洪调度中应加大对班台站点的流量控制.

图7 淮滨与班台固定组合流量下的最可能遭遇组合
2)图7(b)绘制了最可能组合情况变化趋势,可以看出变化趋势出现了明显的阶段性,2000年之前变化缓慢,2000年之后,变化趋势逐渐显著,表明气候变化对洪水遭遇的影响在2000年后日渐显著,未来防洪调度中应充分考虑气候因素的影响,该结论可为各站之间联合调度方案的改进提供重要依据.
3 结论与展望
通过建立淮滨站与班台站年最大日流量及发生时间的联合分布,分析淮河上游与洪河之间遭遇概率及遭遇最可能发生的时间,分析随时间变化遭遇概率等值线的变化情况并计算最可能组合的变化趋势,主要结论如下:
1)以Von Mises函数拟合年最大日流量发生时间,结合Copula函数计算时间联合分布,结果表明遭遇主要发生在7~8月份,7月14日达到峰值0.34%.
2)通过Mann-Kendall检验法表明淮滨与班台站年最大日流量不是一个平稳的时间序列,并以GAMLSS模型拟其分布函数,从量级遭遇概率及遭遇时最可能组合分析淮河干流与洪河遭遇趋势变化.研究表明,以等值线包络线为标准划分风险区较单一等值线更为安全,且随年份增加,遭遇组合呈现淮河干流流量减少而洪河增加的趋势;遭遇概率越低其遭遇组合形式受时间影响程度越大,且班台站受影响程度大于淮滨站;最可能组合中淮河干流流量所占比例逐渐减少为68.0%,而洪河流量增加至32.0%.该结论可为该河段防洪联合调度提供一定的依据,在未来防洪规划中应加大班台防洪调度的重视.
