一个4-D超混沌系统的特性分析及混沌控制设计

梁 媛 王仁明，2 王凌云，2

(1. 三峡大学 电气与新能源学院， 湖北 宜昌 443002； 2. 三峡大学 网络与智能控制研究所， 湖北 宜昌 443002)

超混沌系统一般可以定义为至少存在两个正Lyapunov指数的混沌系统[1]，因而超混沌系统有更复杂的动态行为，如多涡卷混沌吸引子、多个正Lyapunov指数、截面上的Poincare映射非孤立等，这使得对超混沌系统的研究成为极具挑战性的课题．第一个典型的超混沌系统是Rossler超混沌系统[2]，接着其它一些超混沌系统相继出现了，如Chen超混沌系统[3-4]、Lu超混沌系统[5]、Nikolov超混沌系统[6]、Lorenz超混沌系统[7-8]等．

由于混沌系统在许多领域有着明显或潜在的应用，如：保密通讯[9-10]，密码系统[11-12]，加密术[13-14]，电子电路[15-16]等，在过去的20年中，对混沌系统的控制研究受到了极大的关注，出现了许多控制方法：最优控制方法[17-18]，自适应控制方法[19]，滑模控制方法[20]，时滞反馈控制方法[21]等．

基于超混沌系统丰富的动力学特性和实用性，为了更好地对动力学特性进行分析与控制设计．本文讨论了一个新型四维超混沌系统的动力学特性及控制问题．首先，分析了系统的一些动力学特征，如耗散性、时间序列、相轨迹图、李雅普诺夫指数谱和庞加莱映射．接下来，应用Lyapunov稳定理论分析了超混沌系统的自适应控制问题，并对具有完全未知参数的四维超混沌系统设计了一个参数估计的自适应律．最后，利用Matlab仿真软件对所有设计结果进行了仿真验证，阐述了分析和设计的正确性和有效性．

1 系统描述及混沌特性分析

1.1 系统描述

(1)

故本文考虑如下新型四维超混沌系统：

(2)

其中，x，y，z，w为状态变量，a，b，c，d为系统的正常数参量．

1.2 相轨迹和时间序列

当系统参数分别为以下数值时，该四维系统是超混沌的

a=24，b=125，c=5，d=10 (3)

使用Wolf算法计算可知，系统(2)的Lyapunov指数为：L1=2.946，L2=2.083，L3=-2.432，L4=-32.59．由于系统的Lyapunov指数中有两个是正数，说明该新型四维系统是超混沌的．此时，系统(2)的Kaplan-Yorke维数为：

可知系统(2)有一个分数Kaplan-Yorke维数的奇异吸引子．

若取系统(2)的初始状态为：

x(0)=y(0)=z(0)=w(0)=0.2 (4)

则系统的相图、时间序列图及Lyapunov指数谱分别显示在图1、图2和图3中．

图1 四维超混沌系统的相图

图2 四维超混沌系统的时间序列图

图3 四维超混沌系统的Lyapunov指数谱

1.3 耗散性

超混沌系统(2)可以用向量表示为：

(5)

其中，

(6)

通过Liouville定理，可知

其中向量Ω(t)=Φt(Ω)，Φt是f的通量，V(t)为Ω(t)的体积．

系统(2)的散度为：

(8)

其中μ=a+1+c．

根据式(3)中选择的参数值，知μ=30>0，将式(8)里·f的值代入到式(7)中，可得

(9)

即

V(t)=exp(-μt)V(0) (10)

由于μ>0，从式(10)可知，当t→∞时，V(t)以指数方式趋于0．这显示系统(2)是耗散的．因此，其轨线最终被限定于一个零体积的子集内，并且其渐近运动将止于一个奇异吸引子上．

1.4 平衡点

当系统(2)的参数值如(3)中所示时，平衡点可由解下列等式获得：

(11)

即

系统(2)在F∈R4的任一点的雅可比矩阵为：

在平衡点E0的雅可比矩阵为：

(14)

雅可比矩阵J0的特征值数值为：

λ1=-5，λ2=-68.629 0，λ3=0.421 5，λ4=43.207 4 (15)

因此，平衡点E0是不稳定的鞍点．

在平衡点E1的雅可比矩阵为：

(16)

雅可比矩阵J1的特征值数值为：

λ1=-0.362 4，λ2=-23.429 4，

λ3，4=-3.466 5±26.906 7i(17)

因此，平衡点E1也是不稳定的鞍点．

1.5 庞加莱映射

庞加莱映射是一种有助于形象化混沌折叠特性的分析技术．当参数a=24，b=125，c=5，d=10时，在不同的交叉平面，如x=0，z=32，在图4中显示了x-y、y-z和y-w平面对应的庞加莱映射图．

图4 四维超混沌系统的庞加莱映射图

2 4-D超混沌系统的自适应控制

目标是寻找四维超混沌系统(2)的一种具有参数估计值更新规律的自适应控制，使得当t→∞时，所有状态变量x、y、z、w都收敛于系统的平衡点．

假设受控的系统为：

(27)

其中，x，y，z，w为系统的状态变量，且a，b，c，d为未知的参量．V1、V2、V3、V4为待设计的自适应控制器．

若系统(2)的参数是未知的，设计其自适应控制律为：

(28)

参数估计值更新律为：

(29)

这里，a1、b1、c1、d1为不确定参数a、b、c、d的估计值．li(i=1，2，3，…，8)为正常数．则在任意初始状态(x(0)，y(0)，z(0)，w(0))∈R4下，具有未知参数的四维超混沌系统是全局渐近稳定的．

证明：将式(28)代入到式(27)中，可得到如下闭环系统模型：

(30)

定义李雅普诺夫函数为：

将式(29)、式(30)代入(32)中可得：

l7(c-c1)2-l8(d-d1)2

(33)

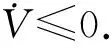
x(0)=2，y(0)=2，z(0)=2，w(0)=2，

a=24，b=125，c=5，d=10 (34)

取li=0(i=1，2，3，…，8)，并设参数的初值为0．状态变量和参数估计值的运行轨迹仿真结果显示在图5和图6中．

图5 自适应控制状态变量图

图6 参数估计值更新图

由图5和图6可看出，在自适应控制器的作用下，系统状态变量迅速趋于平衡点E0(0，0，0，0)，且系统未知参数的估计值收敛于被给的参数值．说明该控制方法对多未知数的四维超混沌系统可以达到期望的控制效果．

3 结 论

本文讨论了一个新型的四维超混沌系统的混沌特性，如耗散性、时间序列、奇异吸引子、李亚普诺夫指数谱、庞加莱映射等．同时，设计了自适应控制律来稳定具有未知参数的新型四维超混沌系统．其设计的有效性和正确性由数值仿真得到了验证．