温度作用下砂岩损伤劣化本构模型研究
2018-11-26靳宝萍王孔伟
靳宝萍 王孔伟 朱 伟 魏 东
(三峡大学 三峡库区地质灾害教育部重点实验室, 湖北 宜昌 443002)
岩石的本构关系一直是岩石力学研究的核心问题,近些年来,国内外学者在岩石损伤理论研究方面取得大量成果.砂岩由多种热膨胀系数不同的矿物成分组成,在对温度变化的响应及敏感性上,表现出显著的差异性,温度作用下砂岩的损伤劣化将对边坡稳定产生重要影响,故研究岩体在温度应力作用下的孔隙水压损伤劣化具有重大意义.
目前研究中,曹文贵[1]根据岩石微元破裂服从正态分布,建立了反映岩石破裂全过程的统计损伤本构模型;邓华锋[2]等基于三峡库区砂岩浸泡-风干循环试验,建立了水岩作用下砂岩损伤统计本构模型;刘桃根[3]等在Burgers模型基础上,应用损伤力学原理,研究了砂岩蠕变损伤模型和参数识别;胡昕[4]等运用统计理论和Lemaitre应变等价性假说,推导出了能反应含水率影响的红砂岩损伤统计模型;王伟[5]等基于室内试验结果与损伤理论,提出考虑流变全过程的流变损伤本菇模型,进行参数识别.从目前的研究成果可知,现阶段考虑温度作用下的砂岩损伤本构关系研究较少.本文根据室内试验结果,基于砂岩试样微元体强度服从两参数的Weibull分布,选取弹性模量作为损伤变量,阐述砂岩在温度及水压作用下的变形破坏及损伤演化过程[6];推导并验证考虑温度效应和水压作用的损伤演化方程及损伤本构模型.
1 温度作用下砂岩力学参数劣化规律分析
本文试验采用TOP INDUSTRIE岩石三轴试验仪,对饱和砂岩进行不同温度及不同渗透水压条件下的常规三轴试验[7-8],试样选自湖北秭归县三峡库区的砂岩.岩样试验条件包括:温度分为5℃、20℃、40℃、60℃ 4个级别,围压分为5 MPa、10 MPa、15 MPa、20 MPa 4个级别,渗透水压分为0 MPa、0.3 MPa、0.6 MPa、0.9 MPa 4个级别.
根据各试样处理后的应力-应变关系分析,发现在15 MPa围压时的曲线最能明显地反映出砂岩损伤劣化力学特性的变化规律,故以下全文均以围压15 MPa时试验结果为研究对象(见表1).
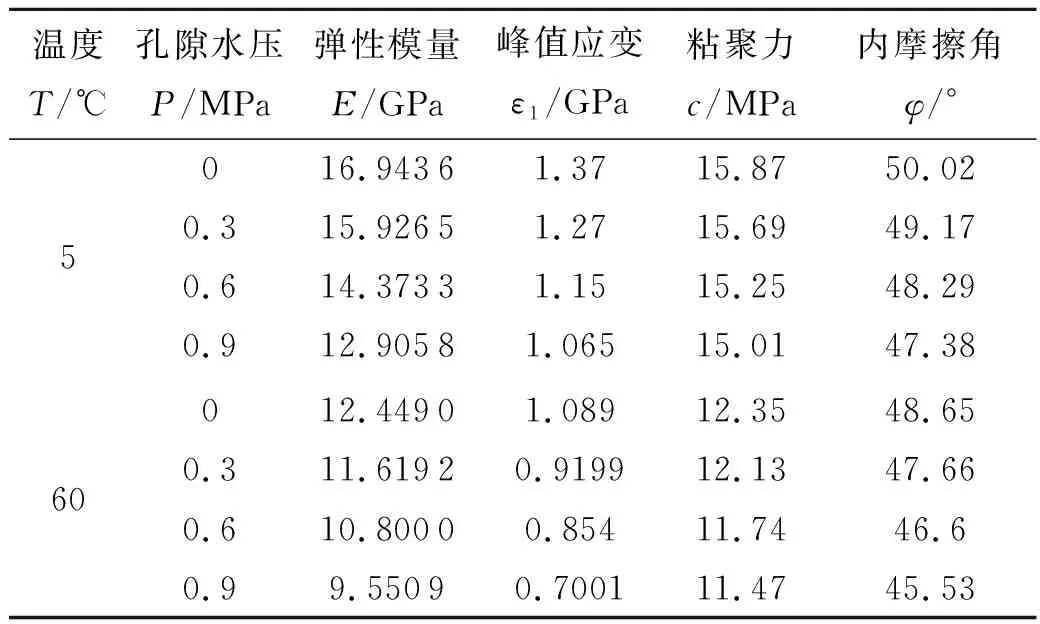
表1 部分试验结果参数表
由表1试验结果分析可知,砂岩在温度作用下,峰值应变、弹性模量、抗剪强度(C、φ)等参数均随温度的升高而降低,温度越高降低幅度越大;在某一恒定温度环境下,峰值应变、弹性模量、抗剪强度(C、φ)等参数均随水压的增大而降低,由此可见,温度与孔隙水压两者的联合作用,会加剧岩石的损伤劣化程度.
在5~60℃温度及0~0.9 MPa孔隙水压条件下,砂岩试样的弹性模量呈现出随温度、围压、水压的变化而变化,即可假设弹性模量是温度、围压及水压的函数,通过函数来拟合弹性模量和温度之间的关系.砂岩试样的弹性模量受温度的影响显著,故本文选定弹性模量来描述砂岩试样在损伤状态时的变量,将热损伤值定义为:
(1)
式中,ET表示为温度T作用时室内试验得出的弹性模量值;E0为初始温度时岩石的弹性模量.
本文不考虑岩石的初始损伤情况,由于岩石各力学指标在不同温度作用下呈弱化趋势,其中5℃时的弱化趋势最不明显,故将5℃时的砂岩试样作为是处于无损伤状态(D=0),即用岩石5℃时的弹性模量作为初始弹性模量E0.
2 考虑温度及孔隙水压作用的损伤演化方程
本试验的砂岩试样均一性较低,其内部分布有大量的初始缺陷(微裂隙、孔洞等),使得试样各微观单元的强度有明显的差异性和在排列上具有随机性,存在较强的离散性,故提出以下假设:
1)岩石内微元体的损伤具有各向同性,基体与损伤体是协调变形的且破坏前符合广义胡克定律;
2)岩石发生弹性变形前的损伤不发展,且其损伤是由温度与孔隙水压共同作用的;
3)岩石在试验之前的初始损伤值为0,随温度升高和孔隙水压增加,损伤值逐渐增加;
4)岩石损伤主轴与应力主轴、应变主轴重合;
5)岩石内各微元体的强度服从Weibull分布及统计规律.
假定砂岩试样的损伤是由其内部微元体的不均匀破坏引起的,设在某一载荷下已破坏的微元体数目为Nf,将已破坏的微元体数目和总微元体数目N的比值定义为统计损伤变量(D=Nf/N),即
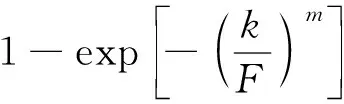
砂岩内部的微观单元体使用摩尔库伦破坏准则来判断是否发生破坏,通式为f(σ)-Q=0,其中Q=ccosφ,φ为岩石的内摩擦角.当f(σ)-Q≥0时,则岩石已屈服或破坏,屈服条件符合摩尔库伦准则:
(3)
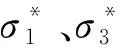
将式(2)代入式(3)中,可得
(4)
根据假设3),岩石微元体在破坏前会服从广义胡克定律,则有
(5)
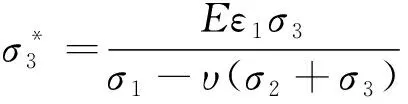
由于本试验σ2=σ3,将式(5)、(6)代入式(4)中,可得
(7)
砂岩的损伤受孔隙水压作用的影响,从该试验结果中可知孔隙水压与弹性模量、内摩擦角之间的关系,与姜桥[9]、胡亚运[10]由胡克定律得到砂岩孔隙水压损伤统计本构方程中的关系式(8)相吻合.
(8)
将其代入式(7),得到砂岩试样在考虑孔隙水压时,其弹性模量的损伤演化方程表达式:
D=1-
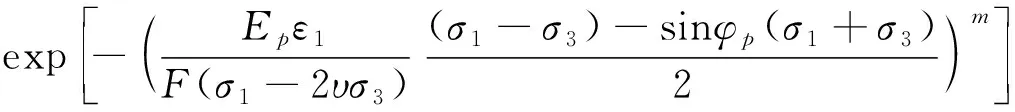
其中,E、φ分别指在没有孔隙水压(p=0)时试样的弹性模量、内摩擦角.
砂岩的损伤还受到温度的较大影响,从三轴压缩试验结果中发现,砂岩试样的均匀性、弹性模量、峰值强度之间在温度变化下存在有某种相似的变化规律.可将砂岩试样的均匀性、弹性模量、峰值强度认为都与热损伤值改变有关.m在Weibull分布中表示形态参数(即不均匀系数),F在Weibull分布中代表岩石的平均强度特征.即
m(T)=(1-DT)m0,F(T)=(1-DT)F0(10)
式中,m0和F0分别表示在温度5℃时砂岩试件的Weibull参数.
将式(10)代入式(9)中,得
(11)
将式(1)代入式(11),整理得到砂岩试样在考虑温度效应及孔隙水压时,其弹性模量的损伤演化方程表达式:
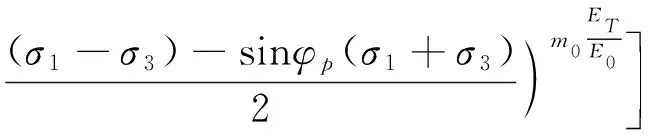
3 温度作用下砂岩损伤统计本构模型
3.1 砂岩损伤统计本构方程
根据应变等效假设式及连续损伤理论、岩石内部微元体在破坏前服从广义胡克定律,再结合本三轴试验的应力条件σ2=σ3进行整理变形得
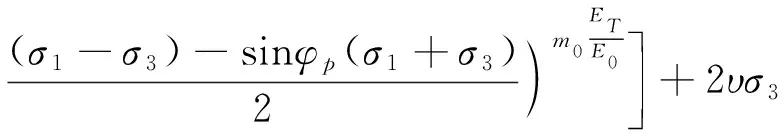
3.2 砂岩损伤本构方程参数的确定
Weibull分布参数m和F的确定是求解砂岩损伤本构模型的关键,一般根据岩石三轴试验时的应力-应变关系曲线来确定.而在砂岩的应力-应变曲线中,存在有峰值强度点,在此点处的导数为0(即其斜率为0),故通过式(13)进行对ε1求一次偏导及变形整理可得:
(14)
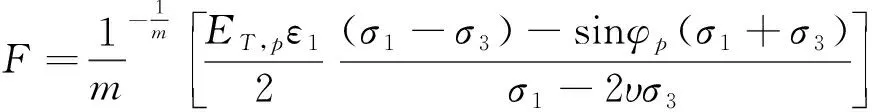
将砂岩试样在不同温度及孔隙水压作用的试验中得到的数据,如峰值应力σ1及对应的最大轴向应变ε1,以及由这些数据求得的E、v、φ等值,代入式(9)、(10)中,并通过曲线拟合的方法,依次求解出损伤本构方程中的分布参数m、F(见表2).
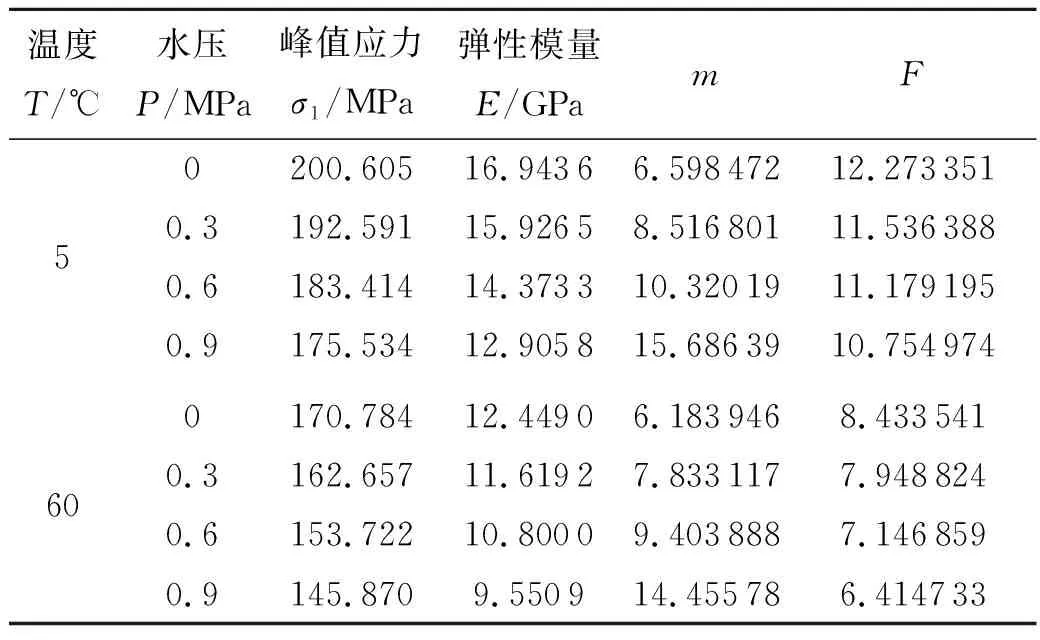
表2 部分砂岩试样试验曲线拟合计算结果
3.3 损伤本构模型的验证
本文选择15 MPa围压条件下,砂岩在不同温度及孔隙水压作用下的试验数据进行损伤本构模型验证.参照胡亚运[7-8]等对岩石损伤本构模型的验证发法,对求得的Weibull分布参数m和F,以及试验数据σ1、σ3、E、p、v、φ、ε1(表2)进行整理,得到σ1-ε1的函数关系,然后分别绘制出在相应试验条件下理论的应力-应变关系曲线,并与实际的试验曲线进行对比,部分曲线如图1~2所示.
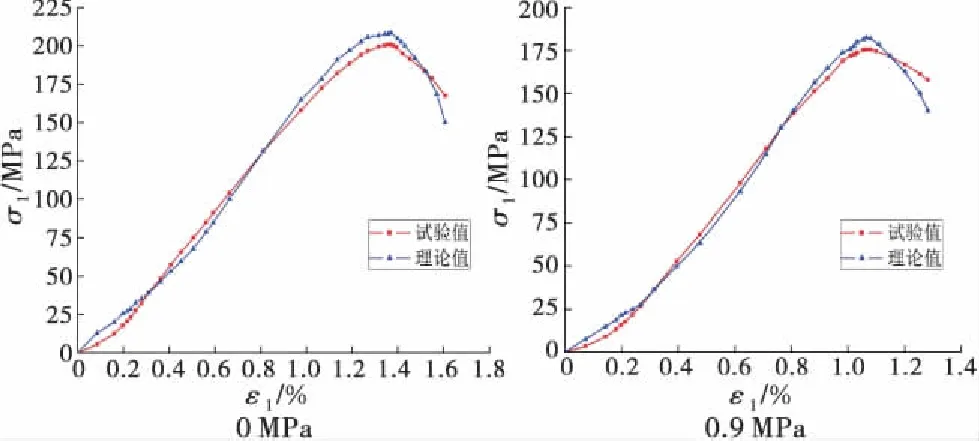
图1 5℃条件下砂岩不同水压时应力-应变曲线试验值与模型值对比图
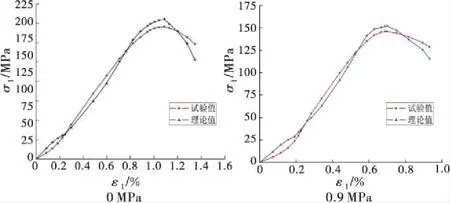
图2 60℃条件下砂岩不同水压时应力-应变曲线试验值与模型值对比图
根据图1~2中理论曲线与试验曲线的对比可得,由本构模型计算出的理论应力-应变曲线与实际的试验曲线的吻合效果较好,两者在不同试验条件下的发展趋势大体一致.
Weibull分布参数中m和F分别反映试样强度和砂岩应力-应变曲线形状,m、F随温度的升高、围压的增大而减小;参数m随水压的增大而增大,参数F随水压的增大而减小.其中,参数F在降低或增大的幅度在降低,表明砂岩试样的强度在逐渐降低或呈降低趋势.
4 结 论
1)通过温度及水压作用相关的损伤弱化理论,假设砂岩试样内微元体的强度服从Weibull概率分布,选取相应的损伤变量来建立了考虑温度效应及孔隙水压作用的砂岩损伤演化方程.
2)通过Lemaitre提出的应变等效假设,在考虑温度效应及孔隙水压作用的砂岩损伤演化方程的基础上,建立了相应的砂岩损伤本构方程.
3)基于试验的结果,由建立的本构模型计算出理论砂岩三轴应力-应变关系曲线与实际试验应力-应变曲线进行对比验证,结果表明二者在一定温度下形状及变化趋势吻合较好,说明了此本构模型有一定的适用性.
