论LM检验的无效性与空间计量模型的选择——以中国空气质量指数社会经济影响因素为例

姜 磊

(浙江财经大学 经济学院，浙江 杭州 310018)

一、引言

自从Paelinck和Klassen[1](1979)首先提出“Spatial Econometrics”(空间计量经济学)的术语以来，经过近40年的发展，空间计量经济学逐渐融入计量经济学领域，成为国际上认可的定量研究经济变量之间关系的模型方法。除此之外，空间计量经济学也大量地应用于自然地理学、人文地理学、经济地理学、区域科学、政治学、社会学等领域。将空间交互效应的概念引入到这些学科领域，成为这些学科领域研究的新视角。

进入2000年以来，应龙根[2](2005)和林光平等[3](2005)学者将空间计量经济学引入到国内，应用中国的数据对中国问题进行实证分析。由此，空间计量经济学正式开始进入到国内的学术界。随后，引起了很多学者的兴趣，涌现出一大批应用空间计量模型对国内的各种经济社会问题展开的实证分析。其中，吴玉鸣[4](2004)首次在博士论文中广泛地应用空间计量模型，为空间计量经济学在国内的推广做出了很大贡献。随后，王立平[5](2005)、李志刚[6](2007)、顾佳峰[7](2007)、周建[8](2008)、柯善咨[9](2009)、张学良[10](2010)等学者也利用空间计量模型对国内的问题开展实证分析。可以说，空间计量经济学的广泛应用，成为继新经济地理学之后推动区域科学复兴的一股新力量(胡安俊和孙久文，2010)[11]。

然而，就目前的研究范式来看，大多数国内的研究在空间计量模型的选择和应用上，既有创新之处，例如将空间计量模型应用于各种学科领域，然而，在空间计量模型选择上又有局限性，对空间计量模型的认识稍显片面。为了更好地推广和普及空间计量经济学在国内学术界的应用，同时也为了疏解空间计量经济学在应用上的一些认识不足。本文主要讨论3个问题：第一，空间计量模型之间的相互联系；第二，拉格朗日乘子检验的无效性和局限性；第三，空间计量经济学模型选择的新思维。

二、空间计量模型之间的联系及模型选择

(一)空间效应

在介绍空间计量模型之前，首先要引入空间效应的概念。空间效应包括空间依赖性和空间异质性，其中，空间依赖性是本文关注的重点。空间依赖性的理论基础是地理学第一定律。具体来说，空间距离相近的事物具有相似性。这种相似性可以通过空间交互作用得以加强。在社会经济现象中，空间范围内相近的空间单元的某种属性值具有相似性被称为空间自相关现象，可以用来描述空间依赖性。空间依赖性体现出了空间交互作用，换言之，空间单元之间存在相互影响的现象。

在介绍计量模型中如何考虑空间交互效应之前，首先引入传统的、不包含空间因素的OLS回归模型，模型为y=Xβ+ε。其中，y表示因变量；X表示自变量，β为待估计的参数；ε表示随机干扰项。可以看出，OLS模型包含3个最基本的组成部分：因变量、自变量和干扰项。相应地，空间交互效应在模型中也分别表现在这3个组成部分。一般来说，空间计量模型与传统计量模型最大的区别在于纳入了空间结构。其中，空间权重矩阵W就是描述空间单元在空间中的组织形式。因此，这3个组成部分的3种空间交互效应可以在模型中分别表示为：Wy、WX、Wε。其中，Wy表示邻近空间单元因变量对本空间单元因变量的影响，被称之为内生空间交互效应；WX表示邻近空间单元的外生变量对本空间单元因变量的影响，被称之为外生空间交互效应；Wε表示的是干扰项中的空间依赖性。这三种空间交互效应包含在计量模型中，形成不同的空间计量模型设定形式。之所以考虑这3种空间交互效应是因为OLS回归后的残差可能存在空间依赖性。在传统的OLS模型中，残差需要满足高斯—马尔科夫定理。但是，却忽略了残差之间可能存在的空间依赖性，如果没有剔除空间依赖性，那么有可能导致有偏且不一致的估计量。

本文主要考虑3种空间权重矩阵：第一，基于地理邻近性的Queen空间权重矩阵(以后简称为Queen)。如果2个空间单元在边界上有共同的点或者边，则认为这两个空间单元相邻；第二，基于距离的空间权重矩阵，计算空间单元两两之间的距离，然后设置门槛值，在门槛值之内的空间单元被认为有空间交互作用(以后简称为Distance)；第三，K个最近邻居的空间权重矩阵，其中K表示邻居的个数，本文K分别选取3到8(以后简称为K3-K8)。前两种为对称矩阵，后一种为非对称矩阵。

(二)空间计量模型概述

一般来说，目前学术界常见的空间计量模型有七种。首先介绍包含因变量空间交互效应的空间计量模型——空间滞后模型(Spatial Lag Model or Spatial Autoregressive Model, SLM or SAR)。由于模型中考虑了因变量的空间滞后项，因而可以很好地描述空间单元因变量的空间交互作用。

另一种常见的空间计量模型为空间误差模型(Spatial Error Model, SEM)，与空间滞后模型不同的是，空间误差模型是由2个公式组成的联立方程，特点是包含了随机干扰项的空间滞后项。

尽管空间滞后模型包含了因变量空间滞后项可以剔除干扰项中的空间依赖性，但是空间滞后模型的残差项依然可能存在空间依赖性。因此，一个更为一般的空间计量模型可以构造出来(Elhorst, 2014)[12]，这个模型也被称之为SAC模型(LeSage and Pace, 2009)[13]。SAC模型涵盖了空间滞后模型和空间误差模型的所有特征。

同样，自变量也可能存在空间交互效应。因此，WX项也可以考虑在模型中，从而形成了自变量空间滞后模型(Spatial Lag of X Model, SLX)。

由于自变量的空间交互效应在实证中普遍存在，那么对于空间滞后模型来说，在考虑了因变量的空间交互效应时，也应该考虑自变量的空间交互作用。这是因为自变量空间滞后项如果在统计上不显著，那么完全不会影响到模型的估计。相反，如果忽略了自变量的空间滞后项，那么可能有遗漏变量的风险(Elhorst, 2014; LeSage and Pace)[12-13]。这种包含了外生解释变量空间滞后项的模型称之为空间杜宾模型(Spatial Durbin Model, SDM)。

同样道理，空间误差模型也可以考虑自变量的空间交互效应，从而产生了另一种空间计量模型：空间杜宾误差模型(Spatial Durbin Error Model, SDEM)。

顺着这个思路，如果在一个模型中同时考虑3种空间交互效应的话，即包含Wy、WX、Wε，那么就形成了一个最为一般的空间计量模型：一般嵌套空间模型(General Nesting Spatial Model, GNS)(Elhorst, 2014)[12]。这7种空间计量模型的具体形式参见图1。

(三)空间计量模型之间的联系

上述介绍了OLS模型和7种空间计量模型，这8种模型之间存在着相互联系(Elhorst, 2014; Vega and Elhorst, 2015)[12, 14],可以归属为同一个模型类别(Family)，如图1所示。

图1 空间计量模型之间的联系

图1最左边的为一般嵌套空间模型，通过对一般嵌套空间模型施加约束条件就可以得到右边的各个空间计量模型。其中，空间杜宾模型可以简化为空间滞后模型或空间误差模型。

由于这8个模型之间是相互联系的，那么，这就产生了一个问题。在实证分析中，究竟是从最左边的一般嵌套空间模型开始分析，还是从最右边的OLS模型开始分析？如果研究的思路是从左到右，则被称为从一般到特殊方法；反之，如果研究的思路是从右到左，则被称之为从特殊到一般方法。在实证分析研究中，两种方法都是可行的。Florax等(2003)[15]建议从经典线性回归模型作为研究的出发点，然后对模型进行扩展。具体来说，从最简单的OLS模型中添加空间滞后项要比从一般到特殊的方法好得多。Elhorst(2010)[16]也非常赞同Florax等(2003)[15]的研究思路。另一方面，从图1来看，也可以从最复杂的一般嵌套空间模型作为分析的开始，这是因为一般嵌套空间模型包含了所有三种空间交互效应。如果空间交互效应在模型中不显著，那么可以简化为其他的空间计量模型。

(四)空间计量模型决策流程

1. 拉格朗日乘子检验判断模型

空间计量模型除了在模型中可以定量地描述空间交互效应之外，更重要的作用是剔除随机干扰项中的空间依赖性。在经典的OLS高斯-马尔可夫定理中，模型回归估计后的残差被认为在空间上是呈现随机分布的，并没有考虑到空间依赖性因素。在对模型进行OLS估计时，如果残差中存在空间依赖性，那么会导致不一致且无效的估计量。因此，检验残差是否存在空间依赖性是空间计量模型分析的重要步骤(欧变玲等，2010)[17]。因此，大多数实证分析以OLS模型作为研究的出发点。

空间滞后模型和空间误差模型由于分别考虑到了因变量的空间滞后项和干扰项的空间滞后项，所以在大多数情况下可以剔除残差中的空间依赖性。为了甄别残差中是否存在空间依赖性，Moran(1950)[18]提出的Moran’s I方法，这种方法简单易行，但是缺点是无法指明选择何种模型。由于存在这2种空间计量模型，为了判断选择，Burridge(1980)[19]和Anselin(1988)[20]基于OLS模型中的残差项构造出了拉格朗日乘子检验(Lagrange multiplier test，LM)用于选择合适的空间计量模型。具体来说是通过LM-Error和LM-Lag统计量来判断选择空间滞后模型还是空间误差模型。实证分析中，在很多情况下LM-Error和LM-Lag统计量同时高度显著，在选择空间计量模型时又出现了选择判断上的困难，为了解决这个问题，Anselin(1996)[21]又提出了稳健性的拉格朗日乘子检验(Robust Lagrange multiplier test，Robust-LM)用于进一步判断究竟空间滞后模型和空间误差模型哪一个是更适合的模型。具体来说，如果Robust LM-Error统计量显著，那么应该选择空间误差模型，如果Robust LM-Lag统计量显著，那么就应该选择空间滞后模型。但是，LM检验的缺点是只能判断模型应该添加因变量的空间滞后项还是应该添加干扰项的空间滞后项。

2. 空间杜宾模型作为分析的起点

作为空间杜宾模型的倡导者，LeSage和Pace(2009)[13]认为空间杜宾模型应该成为研究的起点。这是因为在模型设定中如果忽略因变量的空间滞后项Wy和自变量的空间项WX，可能会造成模型遗漏偏误的问题(Greene, 2011)[22]。相反的是，如果只是忽略了空间自相关误差项Wε，也只是造成了一些效率的损失而已。换言之，估计量仍然具有一致性，但是不再具备有效性。进一步来说，如果数据生成过程即便是其他空间计量模型(除一般嵌套空间模型外)，那么选择空间杜宾模型也不会得到有偏的估计。但是，如果选用一般空间模型作为分析的起点，假若数据生成过程是空间杜宾模型或者空间杜宾误差模型，那么一般空间模型就有遗漏变量的危险。同理，选用空间杜宾误差模型，如果数据生成过程是空间滞后模型、一般空间模型或者空间杜宾模型，那么空间杜宾误差模型也有遗漏变量的危险。

除此之外，选用空间杜宾模型还有一个好处。如果数据生成过程是空间误差模型，那么空间杜宾模型也不会产生错误的标准误和t统计量。这是因为空间误差模型是空间杜宾模型的一个特例。从图1也可以看出，空间杜宾模型在一些条件下可以简化为空间滞后模型或者空间误差模型。换言之，空间滞后模型和空间误差模型是空间杜宾模型的2个特例。

之所以没有选择一般空间模型和一般嵌套空间模型作为分析的起点，是因为这2种模型在实证分析中极为罕见(Elhorst, 2010)[16]，并且在理论解释方面仍然存在一定的问题。换言之，这2种空间计量模型仅仅是作为理论存在的模型。

(五)案例：空气质量指数影响因素

由于不存在普适意义的空间权重矩阵，并且不同的空间权重矩阵也会导致不同的空间计量模型结果(孙洋，2009)[23]。因此，大多数空间计量学者在研究空间计量问题时通常给出一个具体案例。这是因为脱离了实证研究来讨论空间权重矩阵和空间计量模型没有任何意义。具体来说，对于传统的截面数据来说，样本之间是相互独立的，任何排序或者组织形式并不会影响模型的估计结果。然而，对于空间样本数据来说，空间单元在空间上有明显的特定组织结构形式。并且在这种空间结构中，空间单元的某个属性值往往具备一定的相似性，换言之，空间依赖性。也就是说，空间样本数据往往不是相互独立的。此外，空间单元的组织形式也是需要具体问题具体分析，并不存在统一的空间组织形式，或者归纳出公认的空间组织形式的规律。基于上述理由，为了讨论上述LM检验的有效性问题以及空间计量模型选择的问题，本文也给出了一个典型的案例——中国150个城市空气质量指数的社会经济影响因素分析。

中国环境问题日益凸显，尤其是空气污染问题最为突出。近些年，中国饱受长时间、大范围雾霾问题的困扰。并且，经常发生在一些经济发达地区，如京津冀、长三角以及珠三角城市群。空气污染问题引发了公众强烈的反应。为了监测和治理日益恶化的空气质量问题，中国环境保护部发布了《环境空气质量标准》作为新的环境监测标准(中国生态环境部，2012)[24]，其中提出了空气质量指数(Air Quality Index, AQI)作为新的空气质量评价体系。AQI为一个无量纲指标，数值越大，表示空气质量越差，空气污染越严重。AQI提出之后被民众广泛接受，同时也受到了学术界的认可和广泛关注，针对AQI问题开展了诸多研究(高庆先等，2015；蔺雪芹和王岱，2016)[25-26]。

由于数据可获得性受限，本文参考已有的实证研究结果，选取了地区人均生产总值(GDP)、外商直接投资(FDI)、第三产业(Third)、人口密度(Density)、细颗粒物(PM2.5)、和民用汽车保有量(Cars)6个AQI的影响因素。AQI和PM2.5浓度数据为2014年的截面数据，来源于中国环境监测总站。2014年中国在190个城市设立了环境监测站，这其中包括地级市和县级市。本文剔除了县级市，并且由于受限于其他数据的可获得性，最终的样本为150个城市。模型中的FDI数据、地区人均生产总值、第三产业、人口密度、民用汽车保有量来源于《中国统计年鉴(2015)》《中国城市统计年鉴(2015)》和《统计公报(2014)》。

三、实证分析与讨论

(一)空间自相关与讨论

1. Moran’s I检验结果

由于空气污染在空间范围内具有明显的扩散效应，因此，城市间的AQI具备明显的空间集聚现象。与大多数经济社会问题不同的是，空气污染的集聚扩散是一个纯自然的空间交互过程，因而可以判断出城市AQI具备明显的空间自相关现象。在建立空间计量模型之前，首先可以利用Moran’s I指数来进行验证。本文选择Queen空间权重矩阵对150个城市的AQI年平均值进行Moran’s I检验，检验结果发现Moran’s I值为0.639，表现为显著的正向空间自相关。本文还采用了不同的空间权重矩阵进行Moran’s I检验，结果显示均在1%显著性水平下拒绝了“空间随机分布”的原假设，表明了150个城市的AQI存在明显的空间交互效应。

2. 有关空间自相关的讨论

在很多实证分析中，对因变量进行Moran’s I检验是十分常见的。需要说明的是，空间单元上的某种属性在空间上表现出空间自相关现象，有可能是空间交互作用的结果，也有可能是由于统计误差造成的(Anselin, 1988)[27]。前者可以看作是真实的数据生成过程，但是后者是造成虚假空间依赖性的一个重要来源。

由于空气污染存在扩散现象，故此城市间AQI表现出强烈的正向空间自相关。但是，对于大多数社会经济问题来说，这种空间交互作用解释起来通常是模糊的，这是因为有时候在理论上很难解释为什么相邻的空间单元的某种属性值会表现出相似性现象。对于自然地理学来说，地理学第一定律在既定的空间维度和时间尺度上是适用的，但是对于社会经济学来说，人类行为充斥着不确定性和偶然性，并不能用地理学第一定律来进行描述(Barnes, 2004)[28]。如果用地理学第一定律来进行解释，或者简单地描述空间交互效应促使空间集聚现象的形成，很显然是具有争议性的。例如，对于社会经济的一些强外生变量来说，也有可能存在空间集聚现象。例如，中国大陆31个省份的身份证号码开头两位代码明显具有强外生的性质，如果对其进行空间自相关检验，可以发现存在十分显著的空间集聚现象。这个现象除了人为的设定因素之外，不存在任何的空间交互影响。由此可见，对因变量进行空间自相关检验在某些情况下是没有必要的(姜磊，2014)[29]。更进一步来说，空间自相关检验是探索性空间数据分析的一个组成部分，对于社会经济研究来说并不能作为判断存在空间依赖性的唯一依据，更重要的标准应该是理论基础。理论基础应该成为模型选择的重要依据(姜磊，2014)[29]。

在社会经济空间计量实证分析研究中，空间分析应用已经非常普遍(赵永和王岩松，2011)[30]。通常的做法是先进行空间自相关分析，然后进行空间计量建模。这借鉴的是地理学中的空间分析流程，即先是“数据驱动”分析，然后是“模型驱动”分析(Anselin, 1989)[31]。所谓的“数据驱动”就是让数据自己说话(Gould, 1981)[32]，对于社会经济学者来说通常采用的是空间自相关分析。“模型驱动”就是根据理论假设建立合理的空间计量模型。概括来说，目前的空间计量研究也秉承着3类基本的空间分析类别：即空间数据统计分析、基于地图的分析和地理模型和数学(计量)模型(李德仁等，2006)[33]。对于社会经济学者来说，唯一欠缺的可能就是基于地图的分析。诚然，空间数据分析有很多优点，但是探索性的空间数据分析过程也不应该成为模型选择的唯一判断标准。

(二)LM检验结果及分析

1. LM检验结果分析

分析完中国150个城市AQI的空间自相关分析之后，对其影响因素进行分析。城市之间的AQI存在很明显的空间溢出效应，无论是统计检验结果还是实际情况，在分析AQI影响因素时应该纳入空间因素，即考虑AQI的空间滞后项。也就是说，空间滞后模型应当是合适的空间计量模型形式。然而，为了稳健性以及检验判断，本文采用OLS进行回归，然后采用LM检验用于校验上述判断是否正确。OLS回归结果如表1所示。

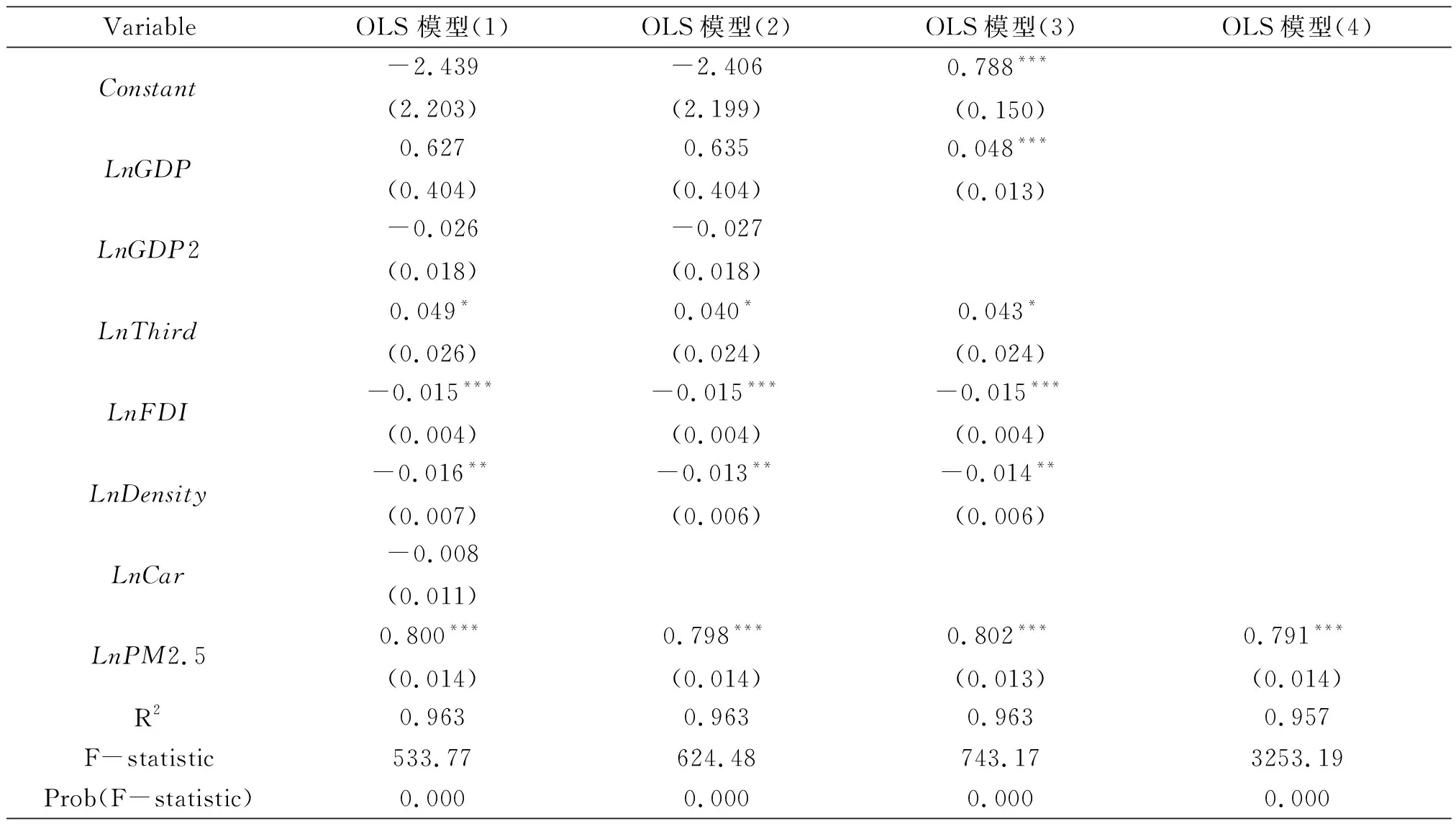
表1 OLS模型估计结果

注：圆括号内为标准误差；***、**和*分别表示1%，5%和10%显著性水平.

表1第2列的OLS模型(1)包含了全部6个变量，由回归结果可知，LnGDP、LnGDP2和LnCar变量高度不显著。LnCar变量不显著的原因跟数据选取有关。剔除了LnCar变量后，回归结果见OLS模型(2)。LnGDP和LnGDP2变量依然不显著，说明不存在倒U曲线。进一步地剔除LnGDP2变量，回归结果见第4列。由OLS模型(3)估计结果可知，所有变量均显著。从拟合优度R2来看，模型拟合程度很好。

OLS模型假设150的城市的AQI观察值在空间上是独立的，这显然违反了地理学第一定律。各个城市之间的AQI并非随机分布。尽管模型应该指向空间滞后模型，但是本文依然给出了5种不同空间权重矩阵情况下的LM检验结果，如表2所示。

表2 LM检验结果

注：方括号内为概率值；K4、K6和K8的结果类似，故此未列.

表2左边为OLS模型(3)的LM检验结果，右边为OLS模型(4)的LM检验结果。对于OLS模型(3)来说，当选择Queen空间权重矩阵时，LM-lag和Robust LM-lag统计量均远远没有通过10%显著性水平的检验，但是LM-error和Robust LM-error统计量高度显著，说明在Queen空间权重矩阵情况下，LM检验结果指向了空间误差模型，而非空间滞后模型。这与选用Queen空间权重矩阵计算出的Moran’s I结果完全相悖。由此可见，即使因变量的Moran’s I表现为正的空间自相关，纳入模型的因变量空间滞后项Wy也可能在统计上不显著。当然，这与空间权重矩阵的选取以及自变量密切相关。

但是，基于距离和K(3-8)个最近邻居的空间权重矩阵的LM检验结果显示4个统计量均高度显著，表明空间滞后模型和空间误差模型均可。这显示，LM检验因选择不同的空间权重矩阵而得出了不同的结论。同时，也说明了不能完全依照LM检验结果来选择模型。LM统计量是根据OLS模型回归后的残差进行构造，通过这4个统计量的构造方式也可以得知，LM检验与所选的空间权重矩阵密切相关。另外，LM检验结果也与自变量密切相关，自变量会影响到回归后的残差，这对LM检验结果同样会产生影响。如果在模型中添加一个高度显著的自变量，很显然会极大地影响到回归后的残差，从而影响LM统计量。对于本例来说，PM2.5变量高度显著，如果只在模型中考虑PM2.5变量，那么LM检验的结果几乎没有任何变化。事实上，4个LM统计量都显著的情况经常发生在空间面板模型的LM检验上。Elhorst(2014)[34]就指出应该考虑空间杜宾模型。稳健性的拉格朗日乘子检验的高度显著是因为显著的空间滞后效应，对于实证分析来说，如果存在高度显著的空间滞后系数，那么这种检验方法就不再有效(Anselin, 1996; 张进峰和方颖，2011)[21, 35]。

2. 空间权重矩阵的讨论

空间权重矩阵是近似地模拟地理邻近性、空间结构和空间关系的一种数量方法，也是空间数据分析和空间计量经济学最重要的核心元素。但遗憾的是，至今仍没有经济学理论、区域科学理论和计量经济学统计检验的方法来判断空间权重矩阵的设定问题(Jiang and Folmer, 2014)[36]。并且，空间权重矩阵的设定也并非具有普适性，因此，针对每一个具体的实证案例应该进行具体问题具体分析。可以说，空间权重矩阵是空间计量经济学和空间数据分析中最强的假设条件。很多学者都认为空间计量经济学最大的一个缺点就是空间权重矩阵无法判定，只能预先设定(Elhorst, 2010; Anselin, 1988; Leenders, 2002)[16,27,37]。

如何提出一个具有普适意义选取空间权重矩阵的方法，一直以来都是很多空间计量学者努力的方向(Kelejian and Robinson, 1995; Griffith, 1995; Tiefelsdorf and Griffith, 1999; Getis and Aldstadt, 2010)[38-41]。孙洋(2009)[42]提出了利用非嵌套的方法来判断空间权重矩阵的优劣，这种方法固然可以针对不同空间权重矩阵的选择有一个统计上的判断，但是也仅仅是停留在统计意义上，很难用理论去解释为什么检验结果所选取的空间权重矩阵优于其他。此外，这个检验还存在另一个问题，就是只能检验针对所选取的空间权重矩阵来进行判断，而没有提出一种如何构造最优空间权重矩阵的方法。更为重要的是，空间权重矩阵的判断不具有普适意义，对于不同的空间结构问题，最优的空间权重矩阵选取的方法也有可能是不同的。另外，地理空间尺度也是影响空间结构的重要因素，可变面元问题(Modifiable Areal Unit Problem，MAUP)也是社会经济学者在空间数据分析和空间计量建模所忽略的问题，会影响到空间分析和空间建模的结果(Openshaw and Taylor, 1979; 杨振山和蔡建明，2010； Arbia and Petrarca, 2011; 陈江平等，2011；齐丽丽和柏延臣，2012)[43-48]。

在实证分析中，有一些学者通常的做法是选取多个不同种类的空间权重矩阵来判断空间计量经济学模型是否对空间权重矩阵敏感，该方法可以看作是敏感性检验在空间计量经济学模型中的一种应用。这种做法的好处是提供了一个至少看起来似乎可以解释的方法。当然，这是在模型对不同种类的空间权重矩阵确实不敏感的情况下可以使用。但是，如果不同的空间权重矩阵导致不同的回归的结果时，尤其是估计的参数因为不同的空间权重矩阵而得出相反的结果时，问题就变得异常复杂。这是由于因为无法判断哪个空间权重矩阵的优劣，进而导致无法判断选择何种空间权重矩阵下的空间计量经济学模型。并且，更为重要的是，在通常情况下解释这种差异有时候是极为困难的。例如，很难解释基于地理邻近性的空间权重矩阵优于基于距离的空间权重矩阵。因此，针对每一个具体的实证案例应该进行具体问题具体分体。空间权重的选取可以严重地影响到LM检验结果，同样也会影响到空间计量模型的估计结果。换言之，LM统计量虽然在某种程度上可以判定空间权重矩阵的适合性，但是产生错误的概率也是较大的(孙洋，2009)[42]。

另一方面，由于空间权重矩阵和自变量均可以影响LM检验结果和空间计量模型的估计结果，因此在遇到空间计量模型设定问题时，可以尝试更换新的空间权重矩阵以及添加新的解释变量(Anselin, 1988)[27]。

(三)空间计量模型的选择

1. 以空间滞后模型为起点的选择流程

国内很多空间计量文献均基于LM检验结果判断空间计量模型，然而LM检验确实存在局限性，并且，LM检验主要针对空间滞后模型和空间误差模型的选择有效(陶长琪和杨海文，2014)[49]。此外，由于LM检验受到很多因素的制约，空间计量模型的选择不只是依赖于拉格朗日乘子检验的结果，还应该结合研究的实际情况和理论基础(姜磊，2016)[29]。因此，LM检验结果同理论相结合，可以作为空间计量模型设定的基本前提。对于本例来说，空间滞后模型应该是非常合适的空间计量模型。本文没有使用推荐的空间杜宾模型作为初始空间计量模型，这是因为自变量的空间滞后项在模型中添加仍然需要稳健的理论基础。

然而，对于本例来说，如果选择Queen空间权重矩阵会发现空间滞后模型的空间自回归系数并不显著，换言之，应该选择空间误差模型。出现这个与事实相悖现象的原因是模型设定的问题。解决这个问题的方法有2个，Anselin(1988)[27]建议选择其他的空间权重矩阵或(和)在模型中添加自变量，直到空间计量模型合理为止。对于大多数研究来说，更换空间权重矩阵相对比较容易，然而由于数据受限的原因，添加解释变量往往极为困难。针对这个问题，本文提出了以空间滞后模型作为起始模型新的空间计量模型决策流程，如图2所示。

图2显示分析的起点模型为空间滞后模型，如果选择更换空间权重矩阵，那么增加自变量或者使用原来的自变量都可以得到合理的新空间滞后模型；如果选择更换空间权重矩阵，那么通过增加自变量也可以得到合理的新空间滞后模型。

图2 以SAR模型为起点的空间计量模型决策流程

对于某些研究来说，当增加解释变量极为困难时，可以选择是否考虑在模型中添加原有自变量的空间滞后项WX。如果选择不添加自变量空间滞后项，那么可以通过添加误差项空间滞后项Wε来剔除干扰项中的空间依赖性。另一方面，也可以通过添加自变量空间滞后项剔除干扰项中的一部分空间依赖性，在很多情况下，这种方式都是有效的。并且，添加自变量空间滞后项也有很多好处，例如，解决了模型遗漏偏误问题。此外，还可以明确地从干扰项中提出一些可能存在的外生影响因素的空间交互效应。如果这些外生变量的空间滞后项在统计上显著，且具备理论基础时，那么可以认为外生影响因素的空间交互效应对因变量产生了影响。但是，当选择空间杜宾模型仍然无法消除干扰项中的空间依赖性时，可以继续考虑添加误差项空间滞后项Wε来剔除干扰项中的空间依赖性，从而考虑一般嵌套空间模型。尽管一般嵌套空间模型包含了所有的空间交互效应，但会使得估计出这些空间交互效应变得复杂。更大的问题在于模型的解释方面，这是由于很难区分一般嵌套空间模型的内生的空间交互效应和外生的空间交互效应(Elhorst, 2010)[16]。

2. 空间计量模型实证分析结果

接下来给出各个空间计量模型回归的估计结果，如表3所示。

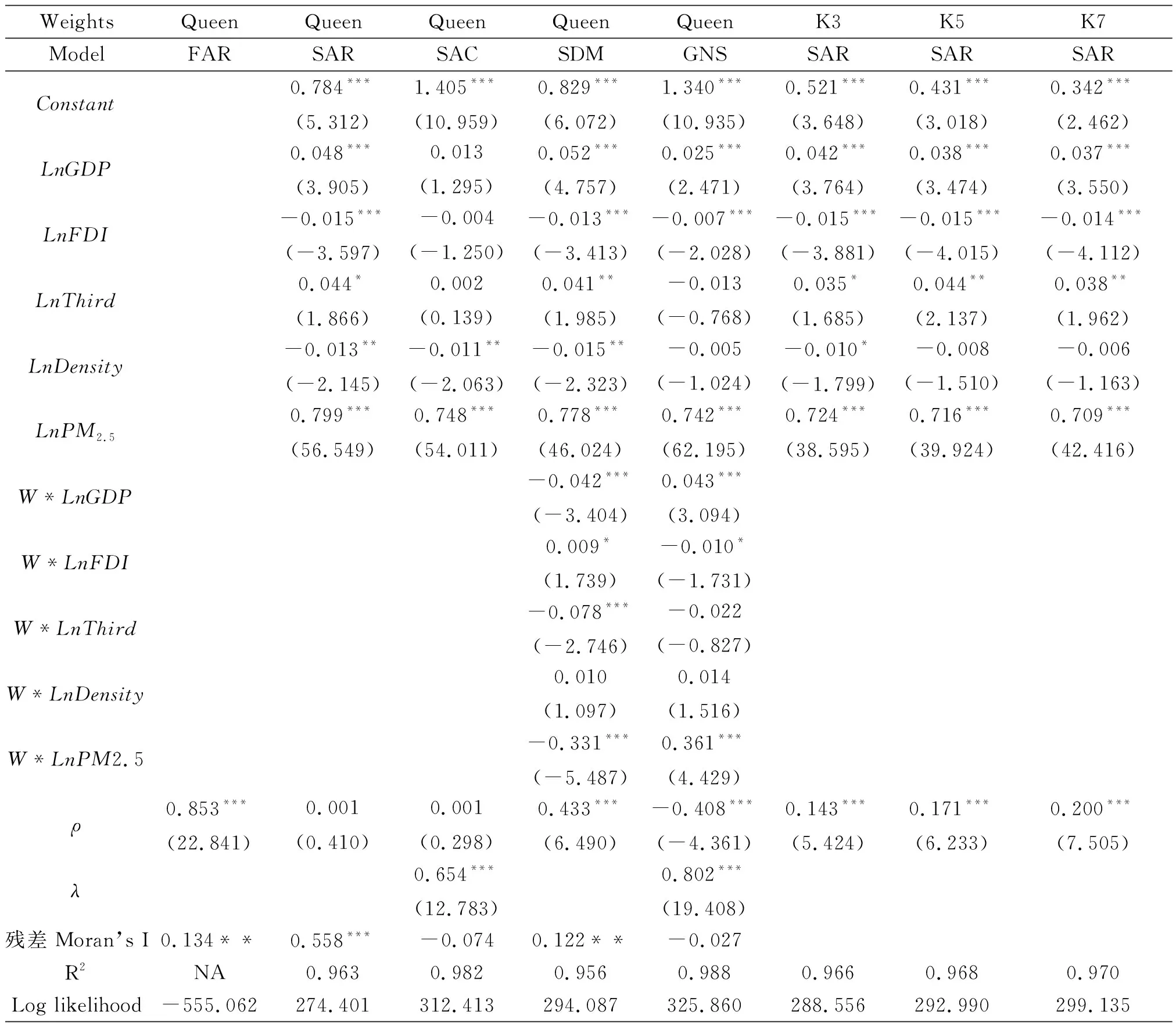
表3 FAR、SAR、SAC和SDM模型估计结果

注：圆括号内为t统计量；***、**和*分别表示1%，5%和10%显著性水平；FAR的R2为负值，由于空间计量模型中的R2与传统计量的定义不同，故此这里的R2不具有比较意义.

表3第2列首先给出了一阶自回归模型(First-order Autoregressive Model, FAR)的估计结果。一阶自回归模型只包含因变量的空间滞后项。由估计结果可知，空间自回归系数ρ高度显著，说明AQI存在明显的空间交互作用。但是对其残差进行Moran’s I检验发现，仍然存在很显著的空间自相关现象(Moran’s I = 0.134)。

第3列展示了空间滞后模型的估计结果，与LM检验结果一致，空间自回归系数ρ不显著。并且，残差的Moran’s I指数高达0.558，存在强烈的空间自相关现象。说明如果选择Queen空间权重矩阵，即便是采用空间滞后模型，也不会消除残差中的空间依赖性。这个结果与LM检验是完全一致的。由此可见，空间权重矩阵不仅会影响到LM检验的结果，也会影响到空间计量模型的估计结果(Florax and Rey, 1995)[50]。

第4列中一般空间模型的估计结果显示空间自回归系数ρ不显著，但是空间自相关系数λ显著，说明干扰项中存在空间依赖性。由于空间自回归系数ρ不显著，因此一般空间模型在Queen空间权重矩阵设定下可以退化为空间误差模型。然而，一般空间模型残差的Moran’s I得分仅仅为-0.074，显示出残差完全不存在空间依赖性，而是在空间上呈现随机分布。说明通过添加干扰项空间滞后项可以完全剔除模型残差中的空间依赖性。换言之，如果选择空间误差模型也可以达到这个目的。这也与之前的LM检验结果是一致的，即如果选择Queen空间权重矩阵，那么应该选择空间误差模型。

通过添加自变量空间滞后项也同样可以剔除干扰项中的部分空间依赖性，由第5列空间杜宾模型的估计结果可知，空间自回归系数ρ十分显著。模型残差的Moran’s I指数仍然比较显著，但是，得分仅仅为0.122，相比较空间滞后模型残差的Moran’s I (0.558)来说有了明显下降，换言之，通过添加自变量空间滞后项可以从干扰项中剔除了大部分的空间依赖性。进一步地来说，如果模型设定合适，有可能通过这种方式完全剔除干扰项中的空间依赖性。

由于干扰项中仍然可能存在空间依赖性，故此可以得到一般嵌套空间模型，如第6列所示。空间自回归系数ρ显著，但却为负数，与基本理论不符，尽管空间自相关系数λ高度显著，也不能称为一个合理的空间计量模型。此外，模型残差的Moran’s I指数也不显著。

由图2可知，也可以通过更换空间权重来实现新的空间滞后模型。本文选择了K个最近邻居的空间权重矩阵。之所以没有选择基于距离的空间权重矩阵，是因为门槛值的设定具有强烈的主观性，并且没有推广的意义。然而，K个最近邻居的空间权重矩阵可以反映出最近几个空间单元对本单元的影响，而且在解释方面非常直观简洁。从K3、K5和K7空间权重矩阵的空间滞后模型估计结果来看，随着邻居数量的增多，空间自回归系数ρ逐渐增大。这也说明了，当选择邻居数过多时，有可能造成空间交互效应的夸大。但是，这只是针对本例而言，这是因为城市AQI具有强烈的空间自相关现象。对于其他案例而言，并非适用。通过Queen和K个最近邻居空间权重的空间滞后模型可以看出，不同的空间权重矩阵也会导致不同的空间计量模型结果。

(四)矩阵指数空间设定模型

上述给出了空间滞后模型在实证分析中如何调整模型，实际上，上述各种模型仍然也没有脱离空间滞后模型的基本框架。因此，在估计方法上采用极大似然估计方法对空间计量模型进行估计。然而，在进行极大似然估计时，涉及到一个含参数的高阶行列式，并且其解析解很难表达，特别是在样本量庞大的时候，因此，通常需要一些特定的技术方法来进行处理(Barry and Pace, 1999)[51]。

针对上述问题，LeSage和Pace(2007)[52]基于Chiu等(1996)[53]在协方差建模中采用的矩阵指数方法提出了矩阵指数空间设定(Matrix Exponential Spatial Specification, MESS)模型，并且证明了MESS模型估计量在理论上的简洁性和计算上的高效性。这是因为MESS模型的矩阵指数的协方差矩阵总是正定的，从而消除了在参数估计中检验要求正定的限制。并且，矩阵指数的逆矩阵也具有简单的数学形式，在理论上和数值计算上皆具备优势，能够灵活地满足空间计量建模的要求。MESS模型不仅具有很好的估计性质，更为重要的是还具备理论优势。MESS模型采用指数衰减来代替传统上的几何衰减，通过设置参数来控制邻近空间单元的数量以及空间溢出作用的衰减程度。MESS模型如公式(1)所示：

Sy=Xβ+ε

(1)

式(1)中，S表示为一个n×n阶的正定矩阵，S矩阵与之前的空间权重矩阵W的含义是一致的。如果令S=(In-ρW)，In表示单位矩阵，那么，MESS模型可以转化为传统的空间滞后模型。接下来给出矩阵指数的形式，如公式(2)所示：

(2)

式(2)中，α表示一个实数参数，W为空间权重矩阵。由公式(2)可以看出，S考虑的是高阶邻近关系影响的指数衰减效应，而并非传统上的几何方式的衰减效应。表4给出了MESS模型的估计结果。

表4 MESS模型估计结果

注：圆括号内为t统计量； ***、**和*分别表示1%，5%和10%显著性水平.

表4第2列显示出了Queen空间权重矩阵MESS模型的估计结果，α的估计系数为-0.001，通过公式ρ=1-eα可以换算出ρ=0.001，这与空间滞后模型(表3第3列)估计的结果是一致的。从上述MESS模型结果来看，选择基于Queen邻近性的空间权重矩阵后折算出的空间自回归系数ρ与空间滞后模型的基本一致。

然而，在这种模型设定下，只是考虑到了空间单元的邻近性原则，并没有考虑到指数衰减效应，换言之，没有考虑到邻近空间单元之外的空间单元的影响。虽然可以通过构造高阶邻近性空间权重矩阵来解决这种问题的，但是仍然存在一个较强的假设：在行标准化的设定下，二阶邻近空间单元对本空间单元影响的强度只是与邻居的个数m有关，而与距离无关。以上海为例来说，上海的一阶邻近城市有苏州和嘉兴，苏州的一阶邻近城市有无锡和湖州，嘉兴的一阶邻近城市有湖州和杭州，剔除重复冗余的空间单元湖州后，那么上海的二阶邻居城市为无锡、湖州和杭州。在行标准化的设置下，无锡、湖州和杭州对上海影响的权重分别为1/3，苏州和嘉兴对上海的影响权重分别为1/2，由此可见，如果高阶邻居数量较少的情况下，那么分配的权重就会变高，从而夸大了高阶邻居城市的影响。

基于这个思想，可以通过构造基于反距离的空间权重矩阵，使得距离越远的城市影响的权重越小。但是，在这种设定下，如果在构造空间权重矩阵时考虑到所有的空间单元，那么每个空间单元都可以与其他所有的空间单元建立起联系。这就存在一个很强的假设：距离即使是很远的城市，也会产生影响，这显然有悖于现实。因此，对于基于距离的空间权重矩阵，可以设置门槛值，即大于门槛值的认为彼此有影响，小于门槛值的被认为没有影响。很显然，这种门槛值的设置带有强烈的主观色彩，因此在大多数实证分析中，会列出基于不同门槛值的回归结果，通过统计量来判断模型的优劣。然而，这种方式得出的结论依然存在过强的主观性。并且在理论上很难解释最优空间计量模型所选取的门槛值。

综上考虑，在本例研究中，城市AQI的影响作用很显然随着距离发生衰减，因此，本文重新考虑了一个更具有弹性的空间权重矩阵，如公式(3)所示。

(3)

式(3)中，φ表示衰减参数，取值范围在0到1之间；m表示最近邻居空间权重矩阵Ni的可变数量，下标i指的是对于第i个最近邻居包含非0元素的权重矩阵(LeSageandPace, 2009)[13]。φi表示第i个个体邻居矩阵施加的相对效应，换言之，MESS模型中的S在构造和使用中依赖于衰减参数φ和邻居数m。

本文基于指数衰减效应估计了AQI影响因素的MESS模型，估计结果如表4所示。基于指数衰减效应的MESS模型涉及到2个重要参数的设定，一个是衰减参数φ，另一个是最大的邻居数m。通过多次模拟发现，MESS模型估计结果对邻居数选择的大小并不敏感。例如，选择3个邻居和选择8个邻居，模型之间的差异极小，然而MESS模型对衰减参数φ的选择十分敏感。表4分别给出了φ=0.3,m=8、φ=0.4,m=7和φ=0.5,m=8三种典型设定的情况，可以发现，当φ=0.5,m=8时，模型的拟合优度最高，对数似然值最大，空间自回归系数也最大。这是因为，当衰减参数φ设置的越小，影响作用随着邻近阶数的增加而迅速衰减，例如，当φ=0.3时，第4阶邻近的影响力只有0.0081，而当φ=0.5时，第4阶邻近的影响力为0.0625，第8阶邻近的影响力为0.0039。通过多次模拟比较发现，当φ=0.5,m=8时模型最佳，并且从MESS模型估计的结果来看(α=-0.152，折算后的ρ=0.141)，与基于3个最近邻居空间权重矩阵空间滞后模型的估计结果很接近(ρ=0.143)(表3第7列)。MESS模型不仅在矩阵求解方面相对于空间滞后模型来说更为便捷，而且在理论解释方面也明显优于基于邻近性空间权重矩阵的空间滞后模型，这是因为不仅考虑到了地理邻近性，还考虑到了衰减效应。

四、结论

在空间计量模型实证分析中，很多研究根据拉格朗日乘子检验作为判断模型的基础。然而，拉格朗日乘子检验统计量的构造与空间权重矩阵以及自变量密切相关。更换空间权重矩阵以及增减自变量均会导致拉格朗日乘子检验结果发生重大变化。尤其是当增减具有强解释能力的自变量时，会引起拉格朗日乘子检验结果明显改变。因此，在实证分析中，仅仅依赖于拉格朗日乘子检验结果作为空间计量模型判断的标准并不准确，应该结合实际情况依据理论基础来选择合适的空间计量模型。

本文利用2014年中国150个城市的样本数据，采用空间滞后模型作为起始模型研究中国城市空气质量指数的社会经济影响因素。并且提出了新的空间计量模型选择流程。对于不能增加自变量的实证分析来说，选择增加自变量空间滞后项，或者考虑添加干扰项空间滞后项均可以剔除残差中的空间依赖性，也可以在模型中囊括这2种空间交互作用，但是一般嵌套空间模型在实证分析中极少应用，并且很难区分内生和外生的空间交互作用。

本文还提出了矩阵指数空间设定模型可以取代应用广泛的空间计量模型。这是因为矩阵指数空间设定模型在模型解释力方面要优于空间滞后模型，并且对于本案例来说，城市间空气污染呈现出空间衰减效应。换言之，对于研究空气污染问题来说，矩阵指数空间设定模型设定了衰减指数和最大邻居数，模型在解释方面不仅优于空间滞后模型，也优于高阶地理邻近性空间权重矩阵的空间滞后模型。对于研究具有明显空间依赖性的环境污染问题来说，矩阵指数空间设定模型具有较为广泛的应用意义。此外，人均地区生产总值、PM2.5浓度和第三产业与空气质量指数呈现正相关关系，而FDI和人口密度与空气质量指数呈现负相关关系。