例谈“综合运用能力”的题组设计

江苏丹阳市华南实验学校东校区 蒋明玉

“题组”一般是指以某一主题情境展开数学问题的设计，通过“一题多问”的方式，达到“一题多变”的效果，取得“一题多思”的目的。“综合运用能力”题组设计一般是给出一段阅读文字材料或图表描述，让学生经历观察、计算、探索、推理、应用等过程，以考查学生综合运用数学知识的能力。在一个主题情境的统领下，精心设计一些有坡度、有联系的题组练习，有利于扩展学生原有的认知结构，突出知识的综合运用，培养学生解决实际问题的能力。设计“综合运用能力”题组，应该以“变化”为主线，在“习题多解、题目变化、功能发挥”上下功夫；应该以“比较”为基点，加强对比分析，同中求异，异中求同，将学生的思维逐步引向深入。

一、“综合运用能力”题组设计以一个主题情境为主线，强调相关联知识的综合运用，可以有效考查学生数学思维的灵活性和深刻性

在某一主题情境的统领下，将各部分有关联的知识以某一情境为主线融为一体，精心设计一些有坡度、有联系的题组练习，有利于沟通知识间的联系，形成知识网络，有利于扩展学生原有的认知结构，突出考查学生的综合运用能力，培养学生数学思维的灵活性和深刻性。

例1 张大叔准备搭建几个大棚用来种植香瓜（如下图）。每个大棚长20米，横截面是一个半径为2米的半圆。请你帮他算一算：

（1）搭建大棚时每0.5米要用一根竹条支撑，那么搭建这样一个大棚共需要 根竹条。

（2）覆盖在这样一个大棚上的塑料薄膜大约要多少平方米？（含两端的横截面）

（3）这样一个大棚的内部空间大约有多大？

（4）像这样一个大棚可种植香瓜的面积是多少平方米？

（5）预测一下，如果每平方米收香瓜15千克，每千克售价3元，那么，这样一个大棚种植的香瓜可卖多少元？

命题简析：这道题的设计，巧妙将侧面积、表面积、容积、面积等概念和公式融合在一起，并且要求学生通过适当的“转化”思想才可以解决上述问题。学生在分析这些问题时，只有通过邻近知识之间的横向比较，从而分清所求实际问题究竟要运用什么数学知识，才能达到灵活运用知识的目的。

例2 做一个圆柱形无盖油桶，底面内直径4分米，高是8分米。

（1）在它四周贴一圈商标纸，需多少平方分米纸？

（2）做这个油桶需多少平方分米的铁皮？（保留整平方分米数）

（3）如果1立方分米可装油0．85千克，这个油桶可装油多少千克？（保留一位小数）

命题简析：通过分析，不难发现：第一个问题是求这个圆柱的侧面积，3.14×4×8=100.48（平方分米）。

第二个问题是求这个圆柱实际用的铁皮面积,即侧面积加上一个底面积。在实际制作中,使用的材料都要比计算得到的结果多一些。因此,要保留整平方分米数,十分位不管是多少,都要向前一位进一。这种取近似数的方法叫作进一法，100.48+3.14×（4÷2）2=113.04（平方分米）≈114（平方分米）。

第三个问题求的是这个圆柱装油量。在实践中,装油的千克数都要比计算得到的结果少一些。因此,要保留整千克数,十分位不管是多少,都要把它舍去。这种取近似数的方法叫作去尾法，3.14×（4÷2）2×8×0.85=85.408(千克)≈85(千克)。

第四个问题则与“分数应用题”相联系，体现了知识的综合运用。

这样，引导学生区分了侧面积、表面积、容积等概念，在解决实际问题的过程中充分发挥了习题的多种发展功能。

命题策略：

1．联系实际生活，培养学生解决实际问题的能力

以某一主题情境由浅入深地安排的题组练习，使学生感到生活中处处有数学，学好数学知识可以解决许多生活中的实际问题，有利于激发学生的学习兴趣，使学生体验到数学知识的广泛应用性。

2．注意知识的综合运用,积极训练学生的数学思维

将各部分有关联的知识融为一体，要求学生灵活选择条件来解决问题，十分有利于训练学生合理选择信息解决问题的能力，使学生能够从整体上把握所学的数学知识，有利于强调和突出知识的综合运用，培养学生思维的灵活性和广阔性。

3．体现训练的层次性，更好地促进学生发展

以某一主题情境由浅入深地安排的题组练习，可以有效运用“一题多变、一题多用”的策略，充分发挥习题的多种发展功能；能够使不同层次的学生都体验到学习的乐趣；有效激发学生学习的热情和积极性，更好地让全体学生都得到不同程度的发展。

二、“综合运用能力”题组设计要善于选择“国内外重要新闻事件”来“捕捉”素材，命题要注意拓宽知识视野，拓展教育功能

我国著名教育家陶行知先生说过：“生活即教育，社会即学校。”选择现实社会生活中发生的重要新闻事件，包括正面社会事件和负面社会事件，合理引入数学命题，让学生用所学的数学知识和方法解释、分析新闻事件。

例3 2014年4月16日韩国“岁月号”沉船惨剧，重新引起了全世界人民对90多年前 “泰坦尼克号”海难的关注。下面两张表格显示了1921年4月15日凌晨“泰坦尼克号”上的乘客人数和后来获救的人数。

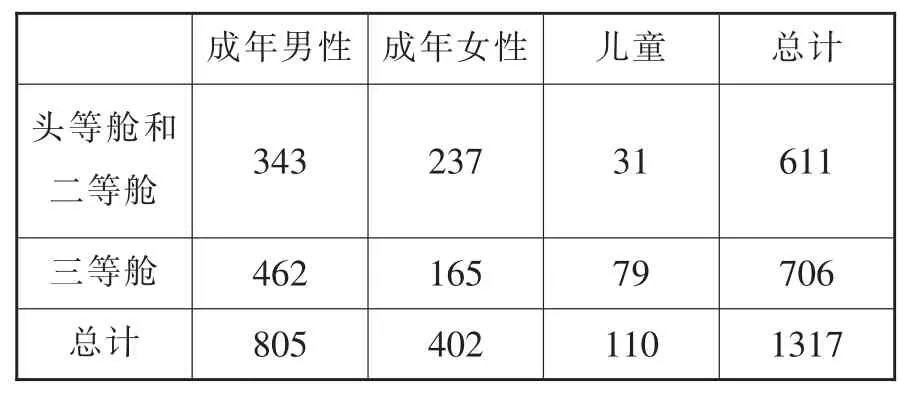
“泰坦尼克号”上的乘客人数

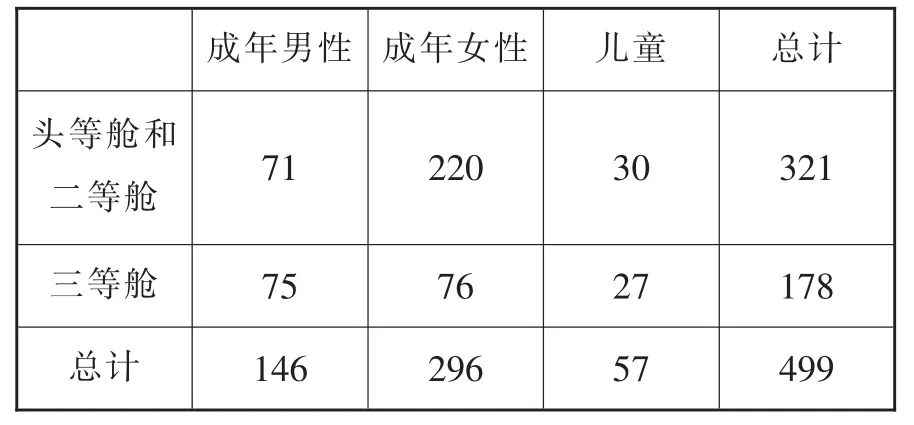
获救的乘客人数

（1）获救乘客占全部乘客的几分之几？

（2）获救妇女和儿童占船上所有妇女和儿童的几分之几？

（3）获救成年男乘客占所有成年男乘客的几分之几？

（4）据当时在场的目击者报告，船员说过“让妇女和儿童优先”这样的话。你认为妇女和儿童真的优先离船了吗？解释一下你的理由。

命题简析：通过计算发现，获救妇女和儿童占船上所有妇女和儿童的，而获救的成年男乘客仅占所有成年男乘客的。对于第4个小问题,学生通过算一算、比一比、想一想，不难发现，超过一半以上的儿童和妇女都获救了，特别是头等舱和二等舱仅有1名儿童没有获救。我们有足够的理由相信：90多年前“在危难时刻让妇女和儿童优先”确实做得很好，值得我们当下好好学习，继续弘扬这种精神。

类似的问题，如在命题中渗透节俭教育：

例4 据调查，我国每年“舌尖”上浪费的粮食相当于粮食总量的。照这样计算：

（1）去年，全国粮食总量约为5000亿千克，而浪费的粮食够2亿人吃一年。平均每人每年吃多少千克？

（2）某县去年的粮食总量约20000万千克，该县一年浪费的粮食够多少万人吃一年？

（3）对这种浪费现象，你有何建议？

还有，在命题中渗透经济教育：

例5 以下是某报报道的一则新闻，请仔细阅读，并解决问题。

怨利润损失卢布报72.197。，今年以来，俄大的货币。鉴于于5年来低位，分析认为，从基本面看，卢布的确难以扭转下跌势头。

（1）在这两个交易日前1美元可兑多少卢布？

（2）“今年以来，俄罗斯卢布跌幅已达五成，成为全球跌幅最大的货币。”你是怎么理解这句话的？

（3）你还能提出什么数学问题？并解答。

再如，在命题中渗透科普教育：

例6 青蛙虽然个头小，本事却大着呢！一只青蛙平均每年可吃掉一万只害虫，而一万只害虫会造成粮食损失0.06吨，每吨粮食的市场价大概是1800元。有人将360只青蛙卖给餐馆，每千克80元，平均每只青蛙重0.1千克。针对这种行为，请你来算一笔账：

（1）360只青蛙卖了多少钱？

（2）吃掉这些青蛙相当于一年损失粮食多少吨？这些粮食能卖多少钱？

（3）算完账后，你有什么感想？

命题策略：

1.发挥试题的教育功能，富有“正能量”

数学命题不仅要关注学生的“四基”和“四能”，同时也要有机渗透环保、科普、经济等思想教育，发挥试题的教育功能，让学生在解题过程中不仅潜移默化地受到了多方面的教育，同时使得学生产生“正能量”。不仅命题的选材要联系儿童实际和生活实际，而且要有益于增长学生的见识，提高学生发现问题、提出问题、分析问题和解决问题的能力，培养学生的应用意识，促使学生用数学知识和数学思维方式观察分析社会。

2.在数学教学中进行德育渗透，关键要靠“数据说话”

依托“综合运用能力”题组设计，结合读表识图，引导学生细心观察生活，从身边发现数学问题，并运用学过的数学知识来解释现象或解决问题，培养学生的信息收集与处理能力。对学生进行德育渗透，靠“道理说教”，不如靠“数据说话”。这样的问题设计，让情感、态度、价值观的教育，自然渗透，润物无声；这样的问题解决，也使“情”与“智”的发展水乳交融、相得益彰。经常这样进行命题，可以帮助学生克服脱离生活、死记硬背、就题论题、纸上谈兵等不良倾向，激发学生学习数学的兴趣，让学生亲近数学、喜欢数学。

笔者结合郑毓信教授 《数学思维与小学数学》一书的学习，认为“好的数学问题”的标准一般有以下几个特点：

（1）具有较强的探索性。与学生实际水平相适应的，大多数学生是“力所能及”的。

（2）具有一定的启示意义。好的问题应当有利于学生掌握相关的数学知识和思想方法，即以思想方法的分析带动具体数学知识的教学，并真正促进学生对于数学基础知识和基本技能的掌握。

（3）具有多种不同的解法，甚至多种可能的答案。即一个好的问题应当具有较大的“开放性”，从而更加有利于学生创新精神的培养。

（4）具有一定的发展余地。即好的问题可以引出新的问题和进一步的思考。

（5）具有一定的现实意义。与学生的实际生活有着直接联系，从而使学生感到数学是一种有意义的活动，也即能够更为清楚地认识数学的价值。

（6）一个好的问题应鼓励、促进同学之间的合作。特别是，能够容忍不同意见并善于欣赏别人，从而能通过积极互动不断取得新的进步。

（7）问题的表述应当简单易懂。特别注意从学生的角度去进行分析，即应当融入学生的生活语言、他们所熟悉的生活现象和事物等。

当然，以上所列举的7条标准显然不可能在每一个问题中都得到充分体现，但这是我们数学教师在命题中应当把握的具体的努力方向。