基于差分隐私保护的谱聚类算法
2018-11-23郑孝遥陈冬梅刘雨晴汪祥舜孙丽萍
郑孝遥,陈冬梅,刘雨晴,尤 浩,汪祥舜,孙丽萍
(1.安徽师范大学 计算机与信息学院,安徽 芜湖 241002; 2.网络与信息安全安徽省重点实验室(安徽师范大学),安徽 芜湖 241002)(*通信作者电子邮箱zxiaoyao_2000@163.com)
0 引言
近年来,随着互联网与信息技术的蓬勃发展,海量数据的产生可以为研究者们提供许多有效的信息资源,对这些海量数据进行挖掘分析可以得到非常有价值的信息,其中聚类分析是有效手段之一,但是在聚类的过程中也存在着隐私泄露的风险。
目前,国内外研究者围绕隐私安全保护问题做了大量的工作,从已有的隐私保护技术来看:k-匿名及其扩展的保护模型技术已被广泛使用。该方法通过存储至少k条记录来隐藏一条数据记录从而达到隐私保护的目的,但是在攻击者掌握特定背景知识的情况下,它就存在不能抵抗一致性攻击的可能。为了克服这一缺点,研究者们不断尝试加以改进而出现了l-多样性[1]、t-邻近[2]、(a,k)-匿名[3]、泛化和随机化[4]等隐私保护技术。
如今关于聚类分析在隐私保护方面的应用越来越多,而且聚类作为数据挖掘和机器学习的主要技术之一被广大学者所研究,聚类分析中常用的隐私保护技术有数值扰动、数值旋转、数值匿名等方法。Oliverira等[5]在2004年提出一种基于新的空间数据转换方法RT(Rotation-based Transformation),该方法的基础是基于几何的旋转变化来隐藏信息,并能保证旋转前后的属性依旧具有有效性;其缺点在于只能对低维度的数据进行变换,维度较高时会损耗数据的真实信息,计算量也较大,并且难以避免一致性攻击造成的隐私泄露。Mukherjee等[6]在2006年针对文献[5]算法不易推广到其他应用场景中的问题而提出了一种新的采用傅里叶变换的数据扰动方法,其优点是在实现敏感信息隐藏的同时能够保持数据值的有效性,并保证欧几里得集中式和分布式场景中的距离精度很高。目前的研究在聚类的基础上加上差分隐私技术的研究还不够成熟,最早提出这一想法的是2005年Blum等[7]给出的利用差分隐私和k-means相结合的算法,使用管理员的身份将噪声引入到查询响应中来维护单个数据库条目的隐私。随后Dwork等[8]在2010年对基于差分隐私的k-means算法进行了更进一步的分析和改进,提出了一种可以计算查询函数和查询序列敏感度的算法。国内的李杨等[9]提出了ε-差分隐私保护下的IDPk-means方法,该方法可以应对攻击者具有任意背景知识的攻击,并且很好地改善了数据聚类后的可用性问题,但是此方法不能解决分布式环境下的隐私泄露安全问题。因此,在2016年李洪成等[10]提出了在分布式环境下满足ε-差分隐私的k-means算法,解决了传统隐私保护模型无法在分布式环境中应对任意背景知识攻击的问题。吴伟民等[11]基于文献[9]提出了满足ε-差分隐私保护的DP-DBScan算法,是应对传统的DBScan聚类算法存在的隐私泄露问题而研究出来的,该算法的实验结果表明与传统的DBScan聚类算法相比,加入拉普拉斯噪声的DP-DBScan算法能保持数据的有效性并实现隐私保护。刘晓迁等[12]基于聚类的匿名化技术,并利用差分隐私保护模型对发布数据进行保护,该方法通过聚类实现匿名化,对匿名分化的数据添加随机噪声来扰动数据的真实值以实现隐私保护,并提高数据的可用性。目前,针对聚类方法结合差分隐私的研究还比较少,本文主要针对谱聚类算法,开展基于差分隐私保护的谱聚类算法研究。
本文主要针对聚类算法存在隐私泄露的问题,利用谱聚类算法将社交关系图网络化,使得具有社交关系的聚类在一起,为了防止这种社交关系泄露,在通过相似性函数计算权重时加上差分隐私的拉普拉斯随机噪声来进行扰动达到隐私保护的作用。
1 相关工作
1.1 谱聚类算法
目前,谱聚类算法在国内得到广泛的应用和研究,最常应用的领域有机器学习、大数据挖掘、图像分割、文本挖掘等[13]。该算法的流程简单,并且与传统的k-means和最大期望(Expectation Maximization, EM)算法相比适用性更强,在任何的数据样本空间中都会聚类出最好的聚类效果。谱聚类的主要思想是基于图谱理论的分割技术,该算法将样本数据看成无向带权图中的一个个顶点,然后利用相似性函数计算出各顶点之间的值,权重值代表各个顶点间的相似度,然后采用图谱的分割准则将数据分割聚类。
一般谱聚类算法的相似性函数采用余弦函数和高斯函数,具体定义如下:
(1)

(2)
图分割算法准则主要有以下几个准则:
1)图分割最小分割法准则:

(3)
2)规范化分割准则:
(4)
3)最小最大分割准则:
(5)
4)比例分割准则:
(6)
谱聚类算法的主要算法流程如算法1所示。
算法1 谱聚类算法。
输入n个数据点集,聚类数目k。
输出 得到k个簇划分。
a)通过高斯核函数的距离公式计算相似性矩阵;
b)利用相似矩阵构建邻接矩阵N和度矩阵G;
c)由第b)步得到的邻接矩阵和度矩阵求出拉普拉斯矩阵L=G1/2NG1/2;
d)得到拉普拉斯矩阵后选取前k个最大特征值对应的特征向量;
e)将特征向量标准化,然后将样本数据点映射到基于一个或多个确定的降维空间中去;
f)基于新的数据点空间,将特征矩阵的每一行看成一个样本点利用k-means将它聚为k类。
1.2 差分隐私
差分隐私保护模型具有严格的数学理论基础,该模型的基本思想是对数据添加噪声来达到隐私保护的目的[14]。该保护方法不需要关心攻击者的强大计算能力和任何的背景知识,即使攻击者拥有除一条记录以外的所有数据记录也能保证这条记录的敏感信息不会被披露,这种机制能够对样本数据中个体敏感信息进行特定的保护,而且还不会引起数据分布的变化。差分隐私的具体定义如下:
定义1 假设数据集D和D′是相邻数据集,两个数据集完全相同或至多相差一条数据记录,给定一个随机算法S,Range(S)是算法S的取值范围,RM是数据集上的输出结果, Pr[X]是事件X的披露风险,则算法S满足ε-差分隐私的保护模型定义:
Pr[S(D)=RM]≤exp(ε) Pr[S(D′)=RM]
(7)
隐私披露风险的值由随机算法S控制,通过限制ε的大小来控制隐私保护的安全度:ε越小引入的随机噪声越大,隐私保护安全性越高;ε越大引入的随机噪声越小,隐私保护安全性越低。
定义2 对于函数F:D→Rd的敏感度定义如下:
(8)
其中:‖*‖1表示一阶范数;F是查询函数;d是记录数据的属性维度;D和D′是至多相差一条数据记录的数据集;R表示的实数空间。
由定义1可以看出随机函数的选择与攻击者的背景知识无关,所以任意一条记录的增加或者删除都不会影响查询结果的输出。该定义从理论上满足了差分隐私对隐私披露风险的要求,而具体的实现还是依靠添加噪声机制来实现。
1.3 两种噪声机制
实现差分隐私保护的噪声添加机制有两种:一种是基于数值型的拉普拉斯噪声机制;另一种是针对非数值型数据的指数机制[15]。
1.3.1 拉普拉斯噪声机制
文献[16]中提出了对于数值型的数据采用拉普拉斯机制对数据的真实值进行扰动来达到隐私安全保护。其定义如下:

Laplace(b)=exp(-|x|/b)
(9)
其概率密度函数表达形式是:
p(x)=exp(-x/b)/(2b)
(10)
其累积分布函数的表达形式是:
D(x)=[1+sgn(x)×(1-exp(x/b))]/2
(11)
其概率密度函数如图1所示。

图1 拉普拉斯概率密度函数Fig. 1 Laplace probability density function
假设数据集为D,查询函数是F,查询结果是F(D),添加噪声的函数为W,其响应值定义如下:
W(D)=F(D)+Laplace(ΔF/ε)
(12)
则称W(D)满足ε-差分隐私保护。
1.3.2 指数机制
Laplace机制仅适用于查询结果是数值型的数据,而在实际的生活应用中许多数据的查询是非数值型的,因此在文献[8]中提出了一种非数值型的算法。该算法定义如下:设随机算法F,查询结果集为R,t是R中某一个体,在这种机制下函数u(D,t)中t是所有输出项的选中项。若算法F以exp((εu(D,t))/(2Δu))的概率从查询结果集中选择并输出的是t,那么称此算法满足ε-差分隐私的保护模型定义。
由此可以看出,当ε越大,被选出输出的概率就越大;当ε较小时,选中输出的概率就变小。
2 差分隐私保护的谱聚类算法分析
2.1 算法描述
与传统的k-means相比,基于图分割理论的谱聚类算法的适用性更强,不容易陷入局部最优解,能够对社交网络中非凸型的数据进行聚类。该算法把数据点看成一个个顶点,然后利用相似矩阵将样本点链接一起,采用子图最优的分割理论来划分。其中相似矩阵计算的是两个样本点之间的权重值,而这种权重可以理解为样本点的亲密度。对于数据的发布者来看,如何在发布数据的同时不泄露它们的亲密度关系是本文的研究重点。因此本文采用差分隐私结合谱聚类的方法,在相似性矩阵上加上满足拉普拉斯分布的随机噪声来达到隐私保护的目的。
基于差分隐私的谱聚类算法流程如下:假设p={p1,p2,…,pn}和q={q1,q2,…,qn}是n维空间中的两个样本集,谱聚类算法的原理就是利用相似性函数计算样本数据集的相似性,值越大相似性越高,聚为一类的可能性就越大。同时这种相似性也可以理解为社交网络中的关系亲密度,为了确保这种亲密关系不被泄露,在计算相似性时加上差分隐私的拉普拉斯噪声来隐藏潜在的数据信息,从而实现隐私安全的保护。
算法2 基于差分隐私的谱聚类算法。
输入 UCI数据集data。
输出 标签label。
1)
定义聚类种类k,根据给定的label计算出k的值;
2)
初始化k_near=100和∂=0.9;
3)
fori=1 torow
4)
forj=1 torow
5)
ifi≠j
6)
dis_matij←exp(-‖pi-qj‖2/(2σ2));
7)
dis_matii←0;
8)
end if
9)
end for
10)
end for
11)
保留k_near的权重值Affinity[i,j],根据积累分布函数(11)生成随机噪声,并添加进去;
12)
计算度矩阵和拉普拉斯矩阵的值du[i,j]、laplas[i,j];
13)
求拉普拉斯矩阵的前k大特征值和对应的特征向量;
14)
15)
利用k-means进行聚类,得到聚类后的label值;
2.2 算法分析

3 实验
3.1 实验数据集
本文采用来自于UCI Knowledge Discovery Archive database (http://archive.ics.uci.edu/)数据集中的liver、 pima、sonar、balance四个数据集进行实验。各数据集信息如表1所示。

表1 UCI数据集Tab. 1 UCI datasets
本文首先对四个数据集liver、 pima、sonar、balance进行预处理,使其每个属性值都在区间[0,1],对四个数据集分别进行谱聚类算法和差分隐私谱聚类算法实验,因为实验的偶然性,所以进行20次实验,对比20次实验结果的平均值。然后调整相似性函数σ的值,如0.1、0.5、0.9、1、2、4、6、8、10和12来确定最佳的聚类状态,并用精确度作为聚类结果的输出。从图2可以看出,聚类效果比较好的σ维持在1~2。
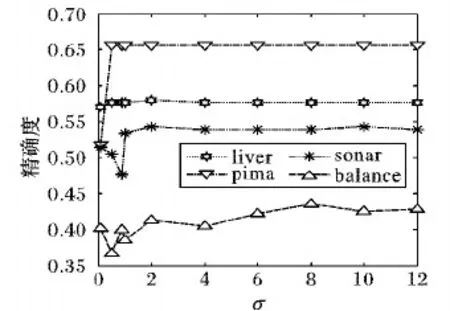
图2 参数σ对聚类结果的影响Fig. 2 Effect of parameter σ on clustering results
3.2 实验配置环境
主要采用Matlab软件编程来实现本文算法。实验的软硬件环境如下:
1)硬件环境配置:Intel i5 处理器,4 GB内存。
2)软件环境配置:Matlab R2013b编程软件,操作系统Windows 7 64位旗舰版。
3.3 实验结果与分析
根据前文的实验设置,本文完成了四个数据集上的对比实验,图3~6分别给出了四个数据集扰动前后的实验对比情况。
由图3可知,对于数据集liver,运用差分隐私的谱聚类算法和只用谱聚类算法在聚类效果上是差不多的,说明本文算法可以在具有隐私保护的前提下,保证了数据集liver的聚类有效性。
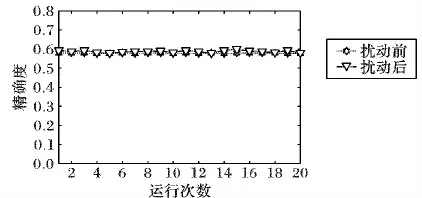
图3 liver数据集扰动前后的精确度结果比较Fig. 3 Accuracy results comparison of dataset liver
由图4可知,对于数据集pima,精确度平均分布在0.6~0.7,分布较为稳定,而扰动前后的对比,虽然总体上是加扰动前聚类效果要好,但是此条件下并不能满足隐私保护,所以扰动后的算法仍然具有可用性。
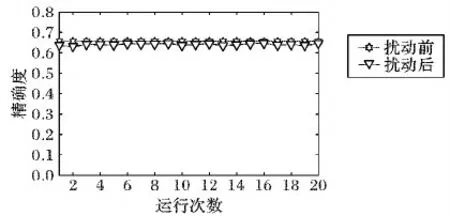
图4 pima数据集扰动前后的精确度结果比较Fig. 4 Accuracy results comparison of dataset pima
由图5可知,对于数据集sonar,其运行的总体情况是加入拉普拉斯噪声要比不加噪声好,精确度平均分布在0.5~0.6,而干扰后的算法在隐私保护的前提下可以达到聚类效果的最好状态。
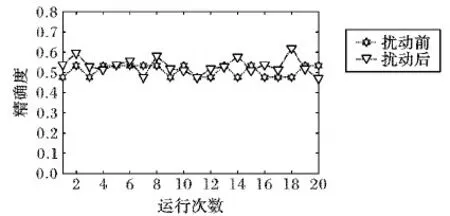
图5 sonar数据集扰动前后的精确度结果比较Fig. 5 Accuracy results comparison of dataset sonar
由图6可知,对于数据集balance的运行结果总体都比未扰动的效果更好,其精确度的平均值稳定在0.4左右,而加入扰动后的值平均在0.5左右,提高了聚类的有效性。同时,经过扰动后的权重因随机点的选取,可能会出现样本点更好的聚类在样本中心点附近,所以出现扰动后结果优于扰动前。

图6 balance数据集扰动前后的精确度结果比较Fig. 6 Accuracy results comparison of dataset balance
对比图3~6,对于不同的四个数据集,在与谱聚类算法和差分隐私谱聚类算法对比实验中,扰动前的精确度总体比扰动后的结果要高一些。总体来说,本文算法在实现隐私保护方面具有较好的成效,同时得到的聚类精确度也较高。
4 结语
本文针对传统的聚类算法存在隐私泄露的风险,以及几个经典的聚类保护算法,如k-means、DBScan、k-medoids等,在社交网络应用中还存在的一些不足,利用谱聚类算法对处理凸型的空间数据和高维度的数据不容易陷入局部最优解的优势,开展具有隐私保护的谱聚类算法研究。首先计算样本数据集之间的样本相似性作为数据点之间的权重值,再利用差分隐私算法对权重值添加拉普拉斯分布的随机噪声,通过干扰权重值达到隐私保护的目的。实验结果表明,干扰后的数据不仅可以实现隐私保护,还保证了聚类的有效性。
