基于多变异策略的自适应差分进化算法

2018-11-23邹德旋

计算机应用 2018年10期

张强,邹德旋,耿娜,沈鑫

(1.江苏师范大学电气工程及自动化学院,江苏徐州 221116; 2.徐州开放大学信息技术与电气工程学院,江苏徐州 221000)(*通信作者电子邮箱uqaing@outlook.com)

0 引言

启发式优化算法本质上是随机性算法,它利用各种随机寻优策略来获得不同优化问题的最优解。在实践领域,很多需要优化的目标函数是不连续的或者不可微的,传统的数学优化方法针对这种情况无法找到较好的解决办法,而启发式优化算法不需要目标函数的连续性和可微性,这就为该算法提供了更广阔的应用空间。近年来研究人员对启发式优化算法的性质进行了研究和分析。到目前为止,已经出现了大量的启发式优化算法,如遗传算法(Genetic Algorithm, GA)[1]、粒子群优化(Particle Swarm Optimization, PSO)算法[2-3]、模拟退火算法(Simulated Annealing Algorithm, SAA)[4]、蚁群优化(Ant Colony Optimization, ACO)算法[5]等。这些计算技术已经被成功地应用于许多实际的优化问题[6-9],在求解最优值的过程中发挥了重要的作用。

在这些优化算法中，差分进化(Differential Evolution, DE)算法[10]于1995年由Storn和Price提出,它是一种随机的、并行直接寻优的优化算法。该方法因具有简单、易实现、鲁棒性强等多种优点,被广泛和成功的应用于函数优化、多目标优化、背包问题、生产调度及其他工程领域。对于进化算法而言,控制参数是该领域研究的核心问题,DE算法也有自身的控制参数。经典的DE算法有3个控制参数:1)种群个数Np;2)变异缩放因子F;3)交叉概率因子CR。相对于其他控制参数而言,Np的变化相对具有普遍性,所以DE算法对于F、CR两个参数的设置更敏感,也是DE算法改进的方向。另外,变异策略对差分进化算法的性能也有很大的影响。本文将从变异策略和参数F、CR的设置为切入点对DE算法进行改进。

1 经典DE算法

DE算法是一种基于群体进化的自组织最小化方法,它的主要思想是引入一种可利用当前群体中的个体差异来构造变异个体的差分变异模式。相对于传统进化算法,差分变异模式是DE算法中最为独特的进化操作。以下简单地介绍经典DE算法的进化过程。

步骤1 种群初始化。

DE算法采用随机方式进行种群初始化,由下面公式产生:

xi, j=xi_min+(xi_max-xi_min)×rand

(1)

其中:rand表示[0,1]内均匀分布的随机数；xi_max、xi_min分别表示每一个向量粒子的每一维分量的上界和下界;i=1,2,…,Np;j=1,2,…，Nd;Np表示种群(向量)个数;Nd表示向量粒子的维度。

步骤2 变异操作。

对给定的当前群体,每一个新变异向量粒子由式(2)产生:

(2)

步骤3 交叉。

(3)

其中:r1～Nd是在区间[1,Nd]中的一个随机整数;CR的取值区间为[0,1]。

步骤4 选择。

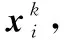
(4)

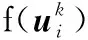
步骤5 判别结束。

如果取得理论最优值或者达到最大迭代次数Ni,则计算结束；否则重复步骤3和步骤4。

2 影响差分进化算法性能的因素

差分进化算法寻优速度和寻优范围存在着相互制约的关系。如果单方面提高寻优速度,虽然能快速得到最优解,但是有可能会陷入局部最优,降低稳定性；反之,如果单方面扩大寻优范围,虽然有利于种群的多样性,防止陷入局部最优,提高算法的稳定性,但是这势必会影响其寻优速度。通常从变异策略和参数设置两个方面来解决这个矛盾。

2.1 变异策略

为了提高寻优的成功率,除了经典的变异策略外,研究者还提出了其他的变种形式。

1)DE/ rand/1/bin:

(5)

2)DE/rand/2/bin:

(6)

3)DE/best/1/bin:

(7)

4)DE/best/2/bin:

(8)

5)DE/current-to-best/1/bin:

(9)

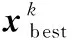
2.2 参数设置

这里的参数主要是针对F、CR。其中F对算法的局部寻优和全局寻优起到一定影响：当F较大时有利于提高种群多样性和提升全局寻优能力;当F较小时有利于提高寻优速度和提升局部寻优能力。而CR是一个阈值,用来决定经过变异的向量粒子能够进入下一步选择操作的数量：CR增大有利于扩大寻优范围,但会降低寻优速度；CR减小会缩小寻优范围,但会提高寻优速度。

从以上分析中可以发现,很难找到一种策略和一种参数设置能够完全解决所有的问题。国内外很多学者对DE算法进行了大量的改进,主要聚焦在三个方面:一是对参数的选取机制的研究[11];二是对差分变异策略的研究,将经典差分进化算法的变异策略串行组合,提出多变异策略差分进化算法[12-13];三是将DE算法与其他算法组成混合算法[14-16]。学者们的改进不同程度地提升了DE算法的寻优性能,但是改进后的算法依然存在寻优精度不高、对不同函数鲁棒性不好等问题。

与此同时,虽然有些学者也提出在DE算法改进中加入学习功能,但是单纯的参数学习就是总结上一次迭代中获胜的向量粒子所用的各种参数,将这些参数直接或间接地用于本次迭代中。经仿真测试表明，这种具有学习能力的改进,可以大幅提高算法的寻优能力；但是对于另外一些函数,特别是多峰函数,存在容易出现局部最优的问题。这是因为在学习的过程中无法确认被学习的对象本身(即上一次迭代获胜的向量粒子)是否已经向局部最优值收敛。从另一个侧面也说明,由于差分算法本质是随机算法的一种,过多人为干预就会丧失或者减弱其原有的特质。这也可以理解为人为干预有利于提高寻优速度,随机寻优有利于扩大寻优范围。为此,本文提出一种基于多变异策略的自适应差分进化(Adaptive Differential Evolution based on Multi-Mutation strategy, ADE-MM)算法。对于多种变异策略的选择,采取的方法是根据学习结果设置扰动阈值,并根据此阈值随机选择每一次迭代中使用的变异策略,因此在学习的过程中又适量地加入扰动因素,做到了有序寻优和随机寻优上的最优结合。

3 ADE-MM算法的改进方法

3.1 变异策略

在ADE-MM算法中共用到三种变异策略:

策略一

(10)

策略二

(11)

策略三

(12)

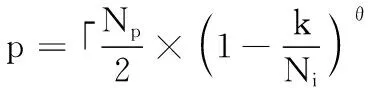
(13)

其中:Np是向量粒子种群个数;Ni是设定的最大迭代次数;k代表当前迭代次数;θ取1.5。根据此公式绘制变化曲线,如图1所示,随着迭代次数的增加,p值逐渐减小。

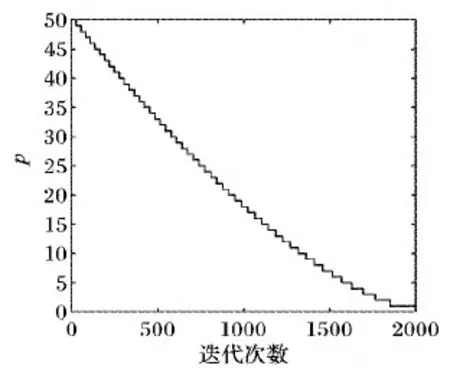
图1 式(13)函数曲线Fig. 1 Formula (13) function curve

结合策略二的变异交叉方式可以看出,当迭代开始时,种群向量粒子的优劣不明显,对于精英粒子来说数量比质量更重要,因此需要p取较大的值来获得较大的寻优范围。但是随着寻优过程的运行,向量粒子的优劣越来越明显,对于精英粒子来说质量反而比数量更重要,需要排名更靠前的粒子来进行局部最优搜索,所以p先大后小。关于三个策略的选择问题,本文中ADE-MM算法引入两个干扰变量B1、B2作为扰动阈值,在一定范围内随机选择,其关系式如下:

(14)

其中：rand1、rand2分别是[0,1]区间内两组均匀分布的随机数。关于B1、B2的取值问题,将在后面讨论。

3.2 学习参数说明

3.2.1 B1和B2设置

(15)

(16)

3.2.2F参数设置

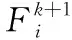
(17)

(18)

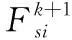
(19)

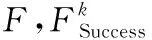
3.2.3CR参数设置

CR与F采用的方法基本一致,分别用式(20)～(22)取得:

(20)

(21)

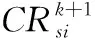
(22)

(23)

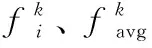
(24)

(25)

(26)

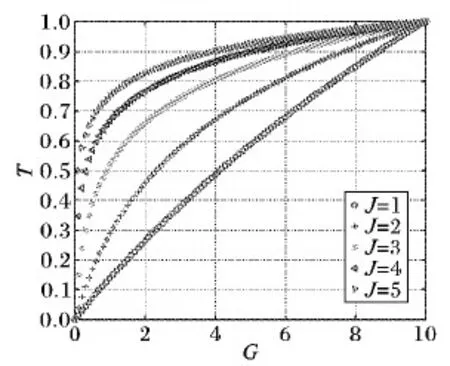
图2 式(25)函数曲线Fig. 2 Formula (25) function curve

3.2.4 其他改进

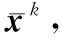
(27)

(28)

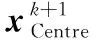
表1 测试函数Tab. 1 Test functions

3.3 算法实现过程

步骤1 参数设置。设置迭代次数Ni;种群规模Np;向量维度Nd;F∈[0.1,0.8];Fsi=0.5;δFi=0.1;CR∈[0.3,1];CRsi=0.6;δCRi=0.1;B1∈[0.9,1];B2∈[0.5,0.6];q=1.5;n=1.5;θ=1.5。

步骤3 变异操作。根据式(14)进行变异操作。如果变异后的向量粒子超出种群设定范围,则重新随机生成这些向量粒子,直至所有种群都在取值范围内。

步骤4 交叉操作。参照式(3)。

步骤5 选择操作。参照式(4)。

步骤6 生成下一代参数。根据选择操作中的比较结果,找出获胜的向量粒子,按照式(15)～(26)产生新的参数,按照式(27)产生向量粒子池,按照式(28)生成用于下一次迭代的中心粒子,并将其加入到下一次迭代的向量粒子群x中。

步骤7 终止判断。当迭代达到最大次数,或者已经寻优出最优值时,算法结束；否则返回步骤3。

3.4 函数与仿真参数设置

为了验证ADE-MM算法的性能,本文选用了8个函数来进行测试。其中：f1～f3是单峰函数,f4～f7是多峰函数,f8是带有平移坐标的函数。这些函数的定义见表1。

此外,为了验证ADE-MM算法在求解无约束优化问题上的优势,将其与随机变异差分进化(Random Mutation Differential Evolution, RMDE)算法[19]、OLCPDE算法以及经典改进算法JADE(Adaptive Differential Evolution with Optional External Archive)[20]、SaDE(Self-adaptive Differential Evolution)[21]、MDE_pBX(Modified Differential Evolution with p-best Crossover)[22]进行比较。根据各种算法在参考文献内的描述,将参数设置如下。

1)RMDE中,缩放因子F=0.5;交叉概率CR=0.3;扰动因子p=0.9。

2)OLCPDE中,缩放因子F=0.5;交叉概率CR=0.8。

3)JADE中,缩放因子F柯西分布的位置参数和尺度参数分别为μF=0.5和δF=0.1;交叉概率CR正态分布的均值和标准差分别μCR=0.5和δCR=0.1;积极的常数c=1;百分比p%=5%。

4)SaDE中,缩放因子F正态分布的均值和标准差分别μF=0.5和δF=0.3;交叉概率CR正态分布的均值和标准差分别μCR=0.5;δCR=0.1;LP=50;p=0.25。

5)MDE_pBx中,缩放因子F柯西分布的位置参数和尺度参数分别为μF=0.5和δF=0.1;交叉概率CR正态分布的均值和标准差分别μCR=0.5和δCR=0.1;q=0.15;n=1.5。

由于学习功能需要对上一代向量粒子进行统计,随着测试维度的增加,向量粒子的个数也应增加以获得更好的学习效果。为了公平起见,针对30维、50维和100维的问题,对于每个测试算法的种群规模Np均分别设置为100、160、300,迭代次数为2 000,独立运行30次。从均值、标准差、Wilcoxon ranksum test、胜率以及算法耗时5个方面来进行分析比较。本文中除Wilcoxon ranksum test利用R语言分析外,其余仿真实验均在Matlab R2016b中进行,内存8 GB,CPU速度为2.4 GHz。

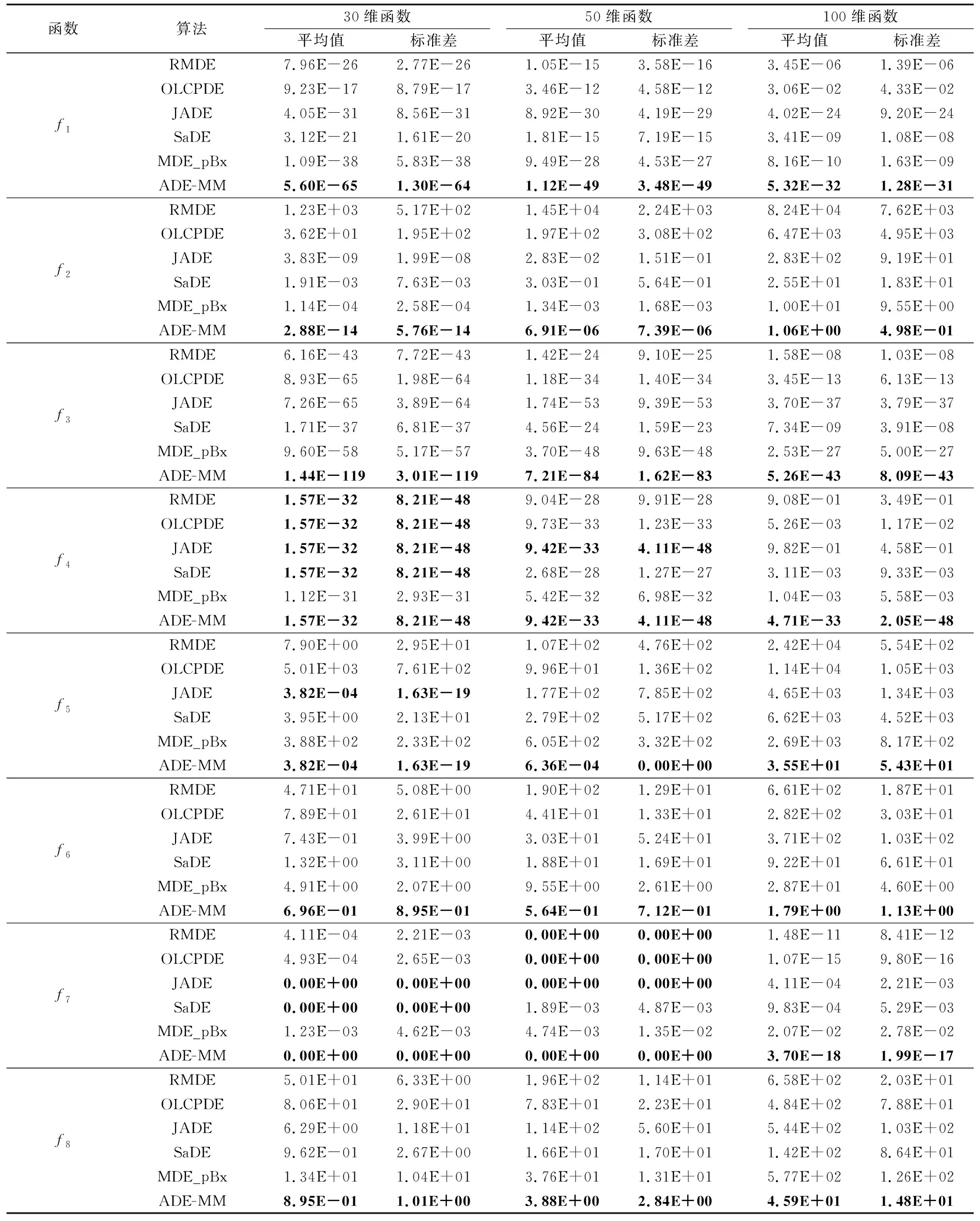
表2 ADE-MM算法与其他算法的均值与标准差计算数据比较Tab. 2 Average and standard variance comparison of ADE-MM and other algorithms

4 仿真实验与数据分析

4.1 均值与标准差分析

表2显示了函数的均值和标准差分别在30维、50维、100维三种的情况下的对比结果。从表2中可以发现,ADE-MM算法取得全胜,其中包括5个函数的单独胜利(f1、f2、f3、f6、f8),3个函数的并列胜利(f4、f5、f7)。为了说明ADE-MM算法在并列胜利的情况下仍具有优势,把这3个函数均值的迭代过程绘制成图3。从图3可以发现,ADE-MM算法在同时都获得最优值的情况下,寻优速度优于其他算法,使用更少的迭代次数,更早地获得最优值。在函数为50维的情况下,ADE-MM算法取得全胜,其中包括6个函数的单独胜利(f1、f2、f3、f5、f6、f8),2个函数的并列胜利(f4、f7)。如图4所示,同样在并列取胜的情况下ADE-MM算法寻优速度要快于其他对比算法。同时在30维的情况下对f4、f5和f7的测试中,与ADE-MM算法并列取胜的对比算法个数分别为4、1和2,而在50维的情况下,变为1、0和3。必须承认,在50维的情况下对f7的测试中并列取胜的对比算法比在30维的情况下多了1个。而在函数为100维的情况下,ADE-MM算法取得全胜,且为单独胜利。因此,总体趋势是随着维度的增加,与ADE-MM算法并列取胜的测试函数个数和对比算法个数均在渐减少,甚至消失。这说明随着函数维度的增加、难度的提高, ADE-MM算法在均值和标准差的比较中的优势更加突显。

图3 ADE-MM算法与其他算法在函数 f4、 f5、 f7的收敛曲线(Nd=30)Fig. 3 Convergence curves of ADE-MM and other algorithms in functions f4, f5, f7(Nd=30)

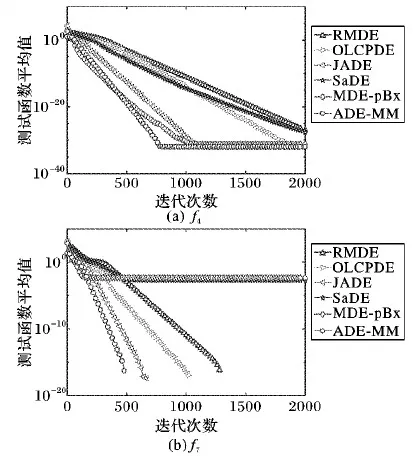
图4 ADE-MM算法与其他算法在函数 f4、 f7的收敛曲线(Nd=50)Fig. 4 Convergence curves of ADE-MM andother algorithms in functions f4, f7(Nd=50)

4.2 Wilcoxon rank sum test分析

下面利用Wilcoxon rank sum test[23-24]对仿真数据进行分析,确定6种算法中的最优算法与其他对比算法是否具有统计学意义上的差异。针对每一个函数取出6种算法中均值最优解的算法,取其每次寻优结果中最优解构成由30个元素组成的基量,同理取其他5种算法每次寻优结果中各自最优解分别构造出5个向量,然后分别与基量进行Wilcoxon rank sum test比较,从中可以获得p-value值。如果得到的p-value小于0.05,说明此算法与最优算法有明显差距;如果得到的p-value大于0.05,则说明此算法与最优算法差距不明显。需要说明三点:第一，均值最优解相同的,利用标准差的比较结果来确定基量。如果均值和标准差都一样,任选一个最优值作为基量,此选择方式不影响最终比较结果。因为在均值比较中ADE-MM取得了全部的胜利,所以基量均来自ADE-MM算法;第二，当两个对比向量相同,且每个向量内元素也相同时, p-value得NaN,需说明的是由于Matlab和R语言的有效值精度问题,此结果无法与之前标准差对应,但不影响p-value实验分析结果;当两个对比向量相同,但每个向量内元素不同时, p-value等于1。以上两个种情况均认为两个对比向量是无差别的。第三， p-value值可以表示最优算法与其他对比算法测试结果存在着“明显区别”和“不明显区别”两种情况,但不能根据p-value值的大小显示同为“明显区别”的结果,区别程度有多大,也不能根据p-value值的大小显示同为“不明显区别”的结果,区别程度有多大。从表3中可以发现,在单峰测试函数f1、f2、f3中ADE-MM算法在3种维度情况下的p-value值均为1,而其他对比算法的p-value值没有出现一个大于0.05,说明此情况下ADE-MM算法不仅在比较中获胜,而且优势明显。在多峰测试函数f4、f5、f6、f7和平移测试函数f8中,从30维的情况到100维的情况的测试中,ADE-MM算法的p-value值全部等于1或者取NaN,而对比算法的p-value值大于0.05、等于1和取NaN的情况在逐渐减少。说明随着维度的增加,能够接近或等于ADE-MM算法的寻优结果的算法越来越少,甚至没有。这进一步体现了ADE-MM算法的优势,特别是解决高维问题时更明显。

4.3 胜率分析

为了展示最优算法与其他对比算法的区别程度,引入胜率进行比较。关于胜率比较作出如下解释:在同一个函数中,分别取ADE-MM算法的30次寻优结果中的每一次数值与其他5种算法的30次寻优结果的每一次数值轮流进行比较,共计进行30×5×30=4 500次,每次比较获胜的一方加1分,结果一样就各加0.5分,输的一方不加分,最后用获胜次数除以比较次数得到胜率,如果胜率超过50%,说明ADE-MM算法在胜率比较中胜出。

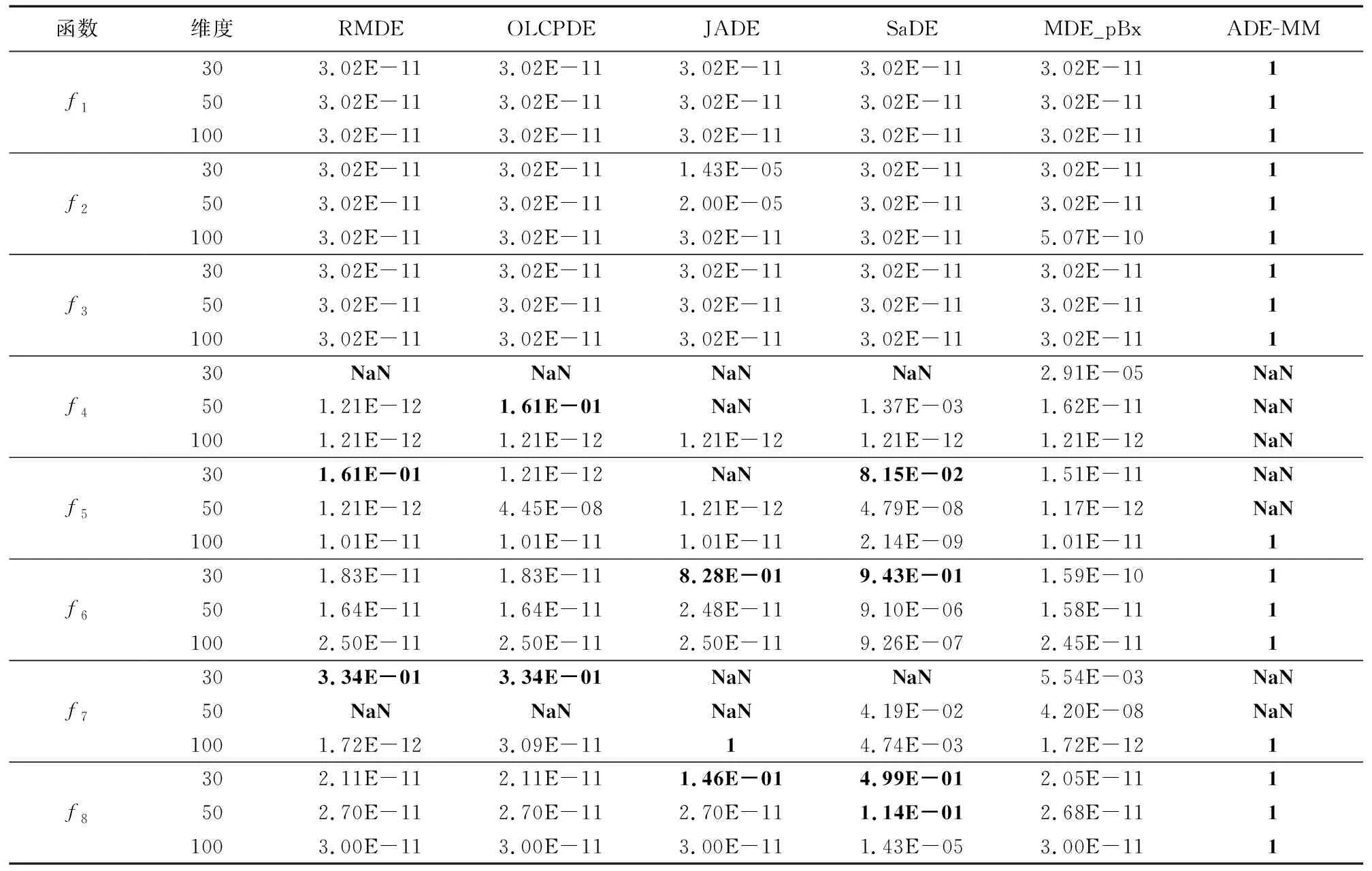
表3 最优算法与其他算法的p-value计算结果Tab. 3 p-value calculation results of the optimal algorithm and other algorithms

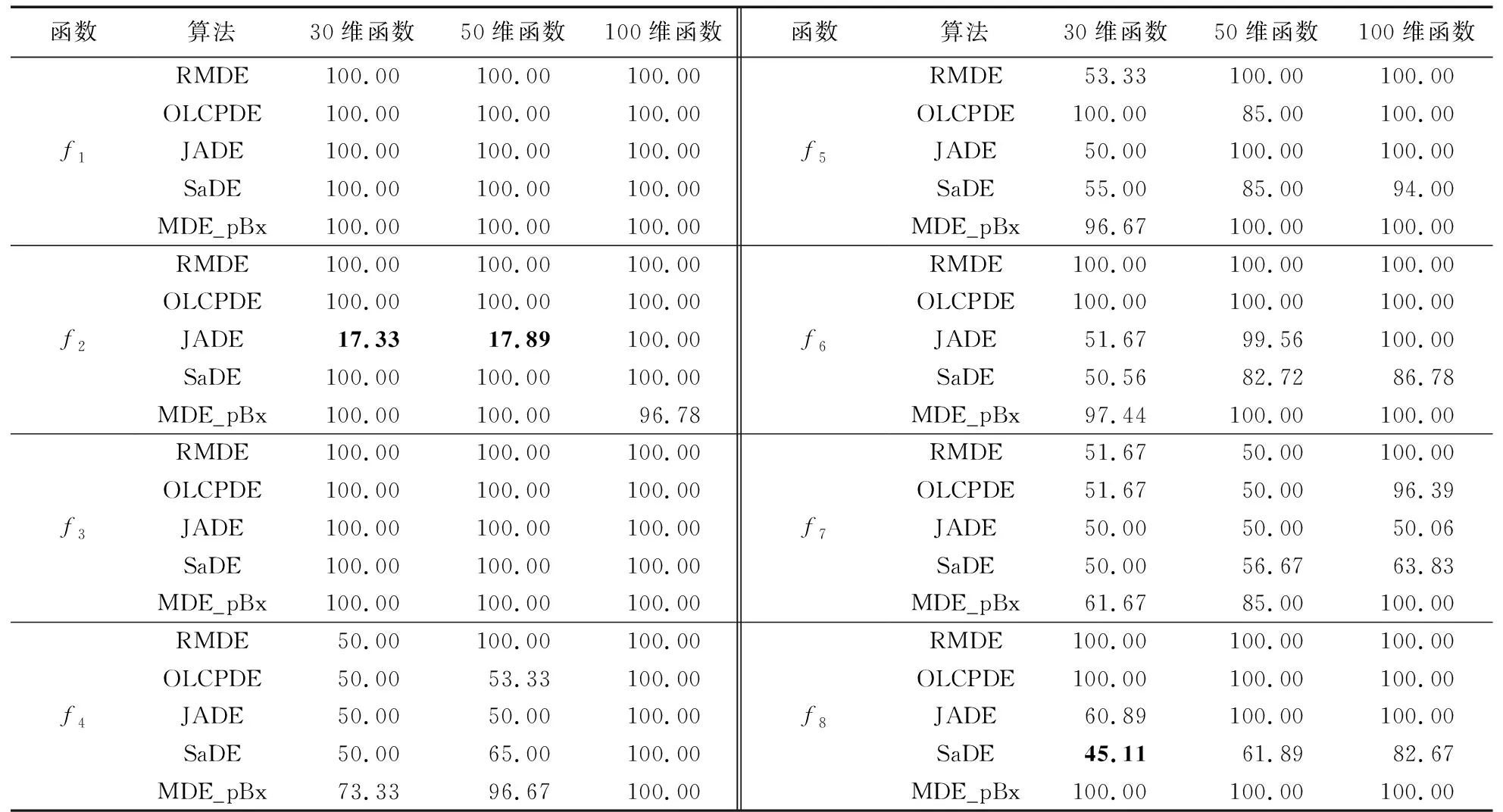
表4 ADE-MM算法与其他算法的胜率计算结果 %Tab. 4 Winning rate calculation results of ADE-MM over other algorithms %

表4中显示的是30维、50维和100维胜率的结果。下面以30维为例,结合均值和p-value值来进行分析。如前文所述,在30维的测试中ADE-MM算法获得全胜,但是从胜率比较中却发现,在函数f2、f8中ADE-MM算法分别输给了JADE、SaDE。下面将以函数f2为例说明出现这种情况的原因。如表5所示,在30维的测试中,JADE算法30次的寻优值大部分优于ADE-MM算法,但是存在3个比较差的寻优结果,最优值和最差值之间有1018量级的差距,这三个较差的寻优结果最终影响了JADE算法的均值。反观ADE-MM算法的30次寻优结果,最优值和最差值之间只有104量级的差距,远远低于JADE的浮动范围,相对稳定,且其最差值比JADE算法的最差值小了106量级。这就解释了为什么ADE-MM算法在对f2、f8测试中,均值比较可以获胜,而胜率比较却失败的原因。通常优化算法的优秀性不仅体现在寻优精度和寻优速度上,寻优稳定性也是重要的衡量指标。这也从另一个侧面显示了ADE-MM算法的优秀性。在100维的胜率比较中,ADE-MM算法在和其他5个对比算法的胜率对比结果均达到或接近100%,此结果与前面均值、标准差和Wilcoxon rank sum test分析结果一致,再次说明ADE-MM算法在解决高维度问题时性能优异。

5 算法耗时分析

由于算法耗时普遍会随着函数维度的增加而同步增加,所以只选取函数为30维的情况来比较各种算法的平均耗时。从表6可以发现,ADE-MM算法对f6和f7两个函数测试用时最少。根据对表2中均值对比,在函数f7的测试中ADE-MM和JADE、SaDE共3种算法同时取得理论最优值0,提前结束迭代。由此可知，在没有获得理论最优值的情况下,运行2 000代ADE-MM算法整体运行时间不是最少的,但是在获得理论最优值可以提前结束迭代的情况下,ADE-MM算法整体用时最少。这说明虽然ADE-MM算法的单次迭代时间不是最短的, 但可以使用更少的迭代次数完成寻优过程。另外,从表6中还可以发现,在8个函数中相比其他对比算法,ADE-MM算法均不是耗时最多的一个。

6 结语

在对差分进化算法改进中,提高寻优速度和扩大寻优范围是一对相对制约的关系,本文提出的ADE-MM算法通过对前一代向量粒子寻优性能的判断与学习来决定下一次迭代中所用到的变异策略和参数设置,以达到增强自适应性和提高寻优速度、精度的目的；同时加入带有学习功能的扰动阈值来改善学习过程,扩大寻优范围,防止向量粒子误入局部最优的陷阱,增强寻优稳定性。本文利用8个函数分别在30维、50维和100维的情况下进行仿真测试,并采用均值、标准差、 p-value、胜率和算法耗时5个指标对仿真结果进行分析。结果表明,ADE-MM算法无论在寻优精度、寻优速度还是在寻优稳定性上都优于其他对比算法,特别是在解决高维问题的优势尤为明显,为解决此类复杂优化问题提供了选择。此外,改进的DE算法已经被应用在路程规划、电力系统经济调度的优化问题中,并且在其中加入约束处理方法,希望能更快速、准确地找到最优的可行解。