超构材料类电磁感应透明现象的实验研究

怀思然，丁亚琼

（上海理工大学 理学院，上海 200093）

在原子系统中，两个量子跃迁通道之间的相消干涉作用会导致光在原子共振频率处的吸收受到遏制并出现一个狭窄的透明窗口，这种奇特的物理效应称为电磁感应透明现象（electromagnetically induced transparency, EIT）[1-2]。但是，量子 EIT 实现非常困难，常常需要超低温度、强磁场，以及大功率的激光器等实验条件。同时，在如此严苛的条件下，量子EIT可调节的参数也有限，这极大地限制了量子EIT的实际应用。近年来，在经典系统中类比电磁感应透明现象引起了科学家极大的兴趣，特别是在超构材料中的类比电磁感应透明现象[3-17]。利用类EIT现象，在室温下就可以方便地实现慢光效应[7-9]；具有高品质因子频谱响应的类EIT现象，可以用来做传感器[10-11]；类EIT现象结构的强色散和全透明，可以用来增强谐振腔的品质因子[12]；量子EIT中一些原本不容易调控的参数，如原子能级间的跃迁频率和自发辐射损耗，在超构材料类比系统中，对应的参量可以通过改变电路参数等方法进行调节，从而有利于研究这些参量对量子光学现象的影响[13-17]。

超构材料实现类EIT效应的原理是量子系统中的三能级原子由超构材料所形成的“人造原子”（“亮态”原子和“暗态”原子）代替，微观量子通道间的干涉被宏观波（光）场之间的干涉代替。“亮态”原子在其共振频率附近可以与入射波（光）发生强烈耦合，用来类比原子三能级系统的激发态；而拥有相同共振频率的“暗态”不能直接与入射波（光）耦合，用来类比亚稳态；“亮态”原子和“暗态”原子之间的耦合可类比耦合光。在类EIT系统中，“亮态”原子由于能够与入射波（光）直接耦合，具有强耗散和低品质因子，损耗主要为散射损耗和吸收损耗。“暗态”不能够直接与入射波（光）进行耦合，只能与“亮态”原子进行耦合，损耗主要来自吸收，并带有较高的品质因子。文献[16]利用一段铜线作为“亮态”原子、两个闭合铜环作为“暗态”原子，通过分别改变“亮态”原子的吸收损耗、“暗态”原子的吸收损耗、“亮态”原子和“暗态”原子之间的耦合强度，实现了电磁感应透明现象向电磁感应吸收现象的转变。文献[17]利用两个嵌套的开口谐振环作为“亮态”原子、一个螺旋谐振环作为“暗态”原子来实现类EIT，得到了随着耦合距离的变大，电磁感应透明频率处吸收率逐渐变大、透射率逐渐变小的结论。

本文利用超构材料中的梳状线结构作为“亮态”原子、开口谐振环作为“暗态”原子来实现类EIT。微带线耦合梳状线结构是原子二能级的经典对应，再添加一个与梳状线耦合的开口谐振环，就构成原子三能级Λ型系统的经典对应。在此结构中，梳状线之所以称为“亮态”原子，是因为其可以直接与入射波耦合；开口谐振环之所以称为“暗态”原子，是因为其距离微带线较远，不能直接与入射波耦合，而是通过梳状线与其发生近场耦合作用。当开口谐振环的共振频率与梳状线的共振频率相同时，就会在此共振频率处出现一个透明窗口[15]。为了使整个结构更加紧凑，在谐振环的开口处加载定值电容。为了便于调节损耗，在谐振环另一端开口并加载电阻。首先通过耦合模方程，从理论上说明电磁感应透明频率处透射率、反射率、吸收率与耦合强度的关系。然后通过实验进行验证。同时还测量了在电磁感应透明频率处的群延时，观察了慢波现象。实验所用结构为平面亚波长结构，便于集成。研究结果可用于设计滤波器及慢波器件。

1 描述类电磁感应透明现象的耦合模方程

利用“亮态”谐振原子和“暗态”谐振原子构建一个类EIT模型。直接与入射波强耦合的“亮态”原子的能量˜ =ae-iωτ和无法直接被入射波激励的“暗态”原子的能量˜ =be-iωτ。其中， e-iωτ表示时间因子， ω为入射电磁波的频率， τ为时间；a，b分别为能量的振幅。假设谐振原子均为单模且“亮态”原子与两个端口均匀地耦合，那么，这个系统的耦合模方程为

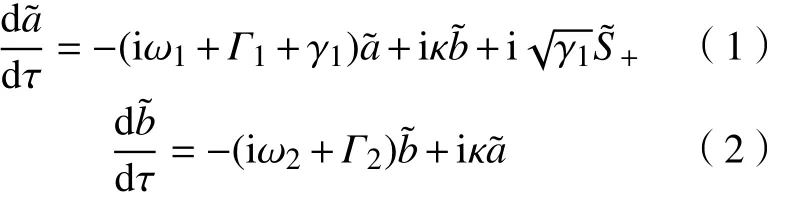
式中： ω1和 ω2分别为“亮态”原子和“暗态”原子的谐振频率； γ1和 Γ1分别为“亮态”原子的散射损耗和吸收损耗； S˜+为入射波； Γ2为“暗态”原子的吸收损耗； κ为“亮态”原子和“暗态”原子间的耦合强度。

当入射波 S˜+=S+e-iωt以频率 ω射入时，解得

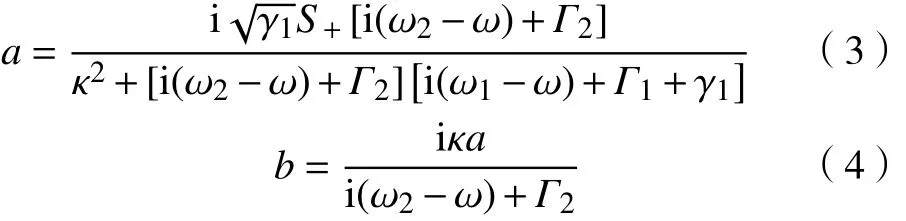
由式（3）和式（4）得到反射系数 r和透射系数t 。A=1-|r|2-|t|2

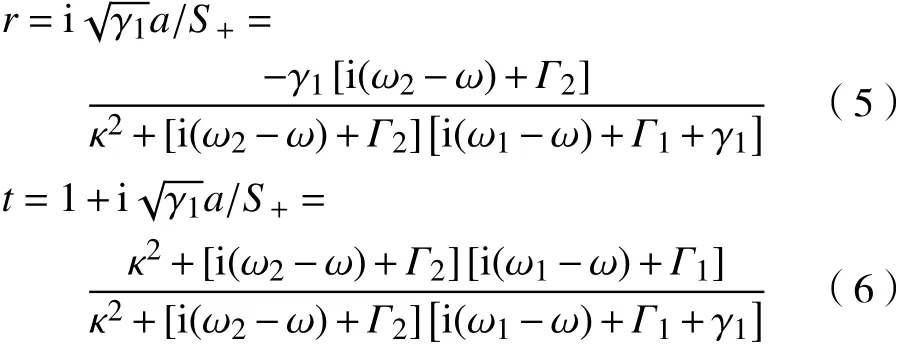
利用吸收公式 可得吸收率

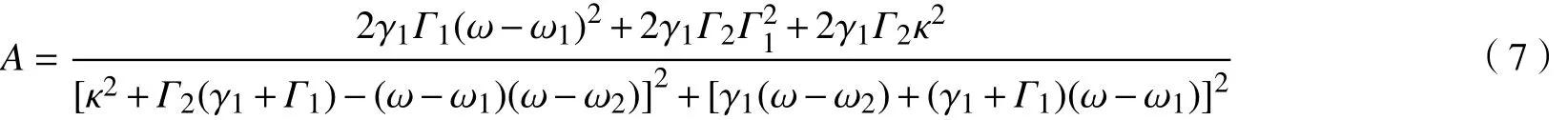
考虑特殊情况，当入射波 S+的频率和两个谐振器的频率相同时，即 ω =ω1=ω2。“亮态”原子的散射损耗 γ1固 定，吸收损耗 Γ1≈0。式（5）～（7）可简化为

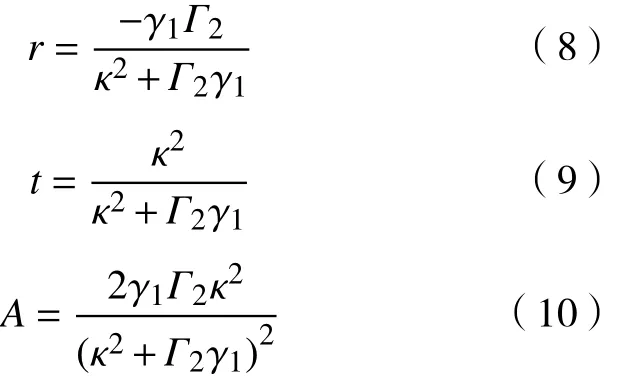
根据式（8）～（10）可以得出：EIT处频率的反射系数r，透射系数t和吸收率A与“亮态”原子散射损耗 γ1， “暗态”原子吸收损耗 Γ2和 耦合强度 κ有关。当 κ2= γ1Γ2时，谐振频率的吸收率达到极值。这3个参数中如果2个参数值不变，只改变其中的1个参数，吸收率会出现非单调性的变化。因为，“亮态”原子散射损耗与“亮态”原子和入射波的耦合强度有关，在实验中不容易改变，所以，在实验中散射损耗 γ1为固定值。在下面的实验研究中，固定“暗态”原子的吸收损耗，研究随着耦合强度的变化，谐振频率处的透射率、反射率和吸收率的变化。

2 实验研究

图1（a）为实验样品图。样品结构采用介电常数为2.2，厚度为0.787 mm的特氟龙（poly tetra fluoroethylene）材质的双面附铜介质板作为基底。由印刷电路板PCB（printed circuit board）技术制备了由梳状线和开口谐振环组成的类EIT超构材料结构。为了满足50Ω阻抗匹配，微带线的宽度为2.4 mm。为了在指定的工作频率（1 000 MHz）工作，设计梳状线的长度l1=59.3 mm，宽度w2=0.3 mm。开口谐振环的大小为l2×l2=8 mm×8 mm方形，线宽w3=0.8 mm，开口处缝宽g=0.8 mm。具体结构参数如图1（b）所示。为了使结构更加紧凑，在谐振环的一端开口处加载了C1=2.6 pF的定值电容。为了便于调节损耗，在另一端开口处加载可调电阻R1。为了使开口谐振环与梳状线发生耦合，谐振环与梳状线距离d比较近。为了使开口谐振环不与微带线发生耦合，谐振环与微带线的距离p比较远，p=18.6 mm。首先通过CST（computer simulation technology）微波实验室仿真软件（microwave studio）计算了单根梳状线的透射谱线，如图1（c）中蓝色点线所示。从图中可以看出，梳状线的共振频率为951 MHz。同样，利用CST软件仿真计算了单个加载C1=2.6 pF电容、R1=1 .5 Ω电阻的开口谐振环的透射谱线（此时开口谐振环与微带线的距离p=0.2 mm），如图1（c）中红色虚线所示。从图中可以看出，开口谐振环的共振频率为952 MHz。梳状线和开口谐振环的共振中心频率非常接近，但是，品质因子差别明显。当两者组合在一起，此时两者间隙d = 0.13 mm，仿真得到EIT样品的透射谱如图1（c）中黑色实线所示。在950 MHz出现了透明窗口，透射系数为0.68。

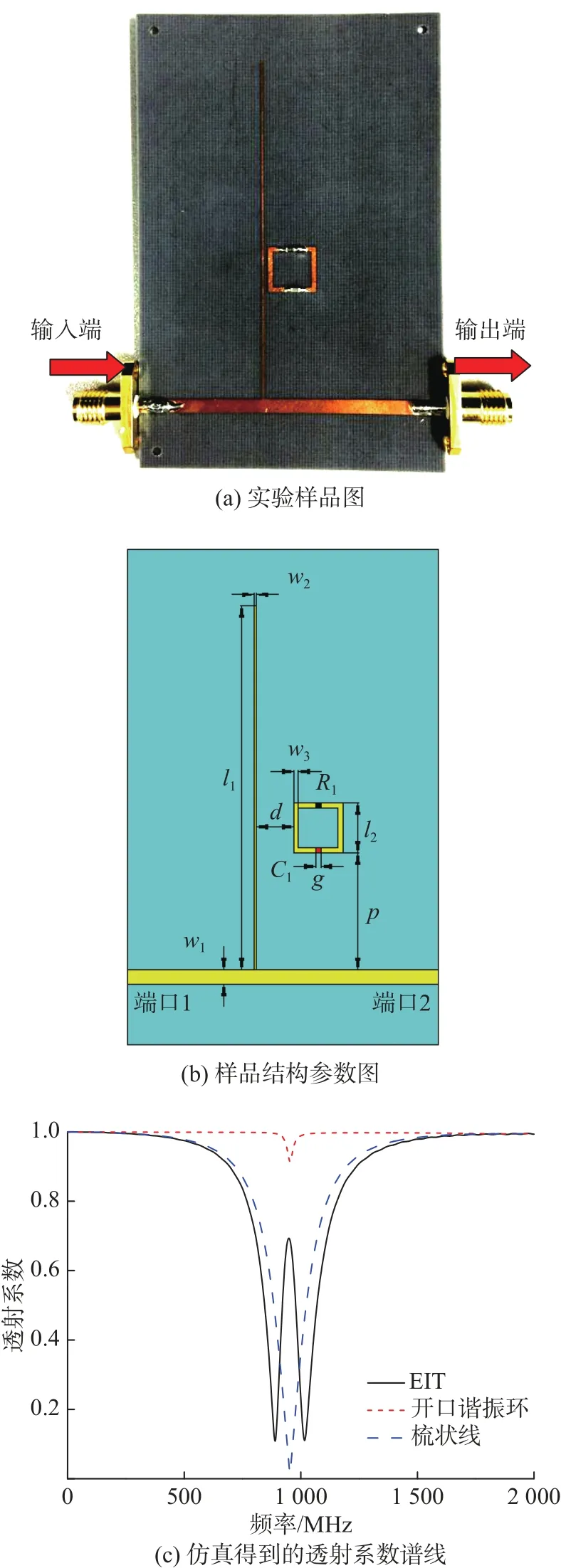
图1 样品图和仿真透射系数谱线Fig.1 Structure and simulated transmission spectra of the sample

从梳状线的透射谱线上可以得到梳状线的散射损耗 γ1=77.2MHz， 吸收损耗 Γ1=0 MHz （吸收损耗主要来源于加所载的电阻。“亮态”不加载电阻，其吸收损耗可以忽略）。开口谐振环的吸收损耗 Γ2可 以通过可调电阻 R1来改变。仿真的样品图如图2中的插图所示。此时开口谐振环与微带线的距离p=0.2 mm，其他参数如前所示。对仿真结果进行线性拟合，得到此样品的散射损耗为3.18 MHz，吸收损耗 Γ2=10.9R1。需要强调的是，在EIT系统中，开口谐振环不与微带线直接发生耦合，因此，不需要考虑散射损耗，只需要考虑吸收损耗。系统的耦合强度与梳状线和开口谐振环之间的距离 d 有关系。 d越大，耦合强度越小。因此，可以通过调节距离 d 来改变近场耦合强度 κ的大小。图3是通过指数拟合仿真数据得到的耦合强度 κ和 距离 d的函数关系图。从图中可以看到，随着耦合距离 d 的增大，耦合强度 κ呈现出非线性的减小，开始减小得比较快，逐渐趋于平缓。为了达到较好的实验结果，固定暗态的吸收损耗 Γ2=19 .5 MHz，即开口谐振环上加载1 . 5Ω的电阻，选出3组不同的 距 离 参 数 d =0.13 mm(κ≈ 65MHz)， d=0.4 mm(κ≈ 40 MHz)和d=0.7 mm(κ≈ 25 MHz)。3组样品都如图1（a）所示，所不同的只是距离参数 d。

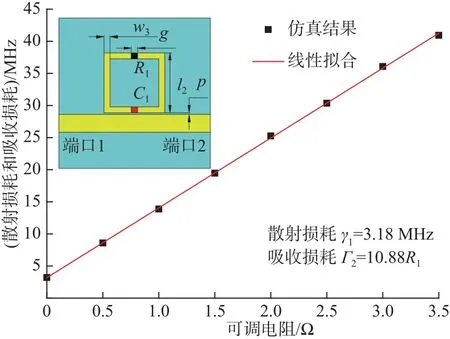
图2 开口谐振环吸收损耗与加载电阻的关系（插图为开口谐振环示意图）Fig.2 Relationship between the absorption loss of the splitring resonator and the loaded resistance（The inset presents the schematic of the split-ring resonator）

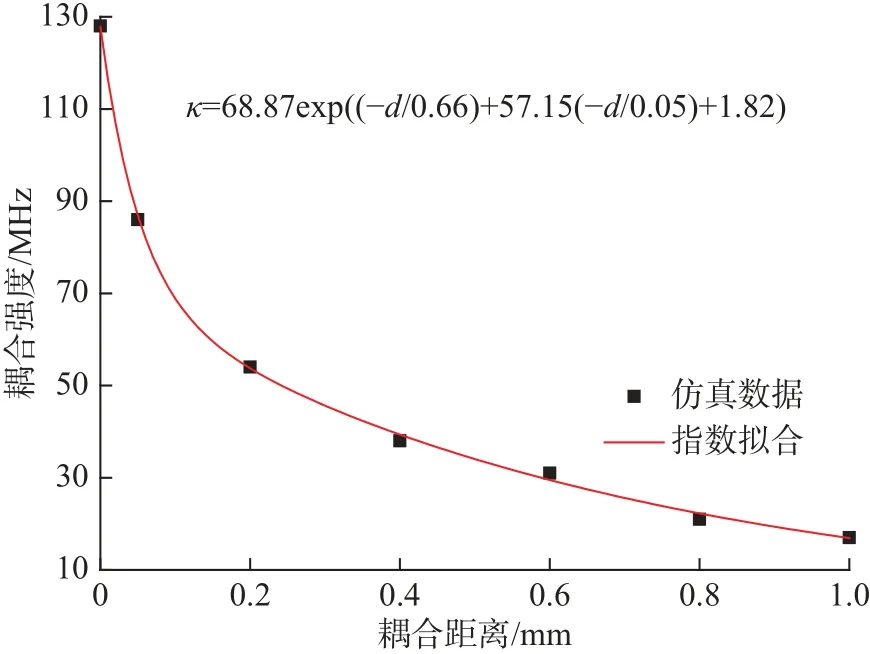
图3 开口谐振环与梳状线之间耦合强度与耦合距离的关系Fig.3 Relationship between the coupling strength and the coupling distance in the EIT element

利用安捷伦公司的型号为N5244A的网络矢量信号分析仪测量3个EIT样品（分别为 d =0.13，0.4，0.7 mm）的透射率、反射率和吸收率。实验与仿真结果如图4所示（见下页）。黑色实线为实验结果，红色虚线为仿真结果。实验测定的EIT透射频率在960 MHz附近。图4（a）为不同距离（即不同耦合强度）下的反射率谱线。从图中可以看到，实验结果和仿真结果符合得很好。随着耦合距离的增大，EIT透明窗口反射谱线宽度变得越来越窄，反射率逐渐增大。图4（b）为不同距离（即不同耦合强度）下的透射率谱线。实验结果和仿真结果相吻合。从图中可以看到，随着耦合距离的变大，EIT透明窗口透射谱线宽度变窄，品质因子变大，EIT透射频率处透射率逐渐减小。图4（c）为不同距离（即不同耦合强度）下的吸收率谱线。实验结果和仿真结果相符。从图中可以看到，随着耦合距离的变大，EIT透明窗口吸收谱线宽度变窄，品质因子变大，EIT透射频率处吸收率呈现先上升后下降的趋势。这种现象可以根据前面的耦合模理论进行解释。类EIT系统的反射系数、透射系数和吸收率与梳状线的散射损耗 γ1，开口谐振环吸收损耗 Γ2和 耦合强度 κ有 关。在实验中， γ1和梳状线与微带线的耦合强度有关，为固定值。Γ2与加载在开口谐振环上的电阻有关，同样为固定值。因此，反射系数、透射系数和吸收率仅与耦合强度 κ有关系。反射率等于反射系数的模平方。根据式（8），在共振频率处，随着耦合强度的减小，反射系数的模呈现非线性增大，即随着耦合强度的减小，反射率呈现非线性的增大。根据式（9），在共振频率处，随着耦合强度的减小，透射系数呈现非线性减小。根据透射率等于透射系数的平方，可以得到，随着耦合强度的减小，透射率呈现非线性的减小。根据式（10），在共振频率处，随着耦合强度的减小，吸收率存在极值。当d=0.13 mm(κ≈65 MHz)， κ2＞， γ1Γ2不是极值点；当 d =0.4 mm ( κ ≈ 40 MHz)， κ2≈ γ1Γ2，吸收率在极值点附近 ； 当 d =0.7 mm(κ≈ 2 5MHz)， κ2＜ γ1Γ2，吸收率远离极值点，从而得到在EIT透明频率处吸收率呈现先增大后减小的趋势。吸收率同开口谐振环上的场局域有关系。因此，开口谐振环上的场局域也是随着耦合强度的减小，出现先增大再减小的趋势。文献[17]研究了随着耦合强度的变化，EIT频率处的吸收率呈现的单调变化是因为没有考虑到吸收率的极值点。

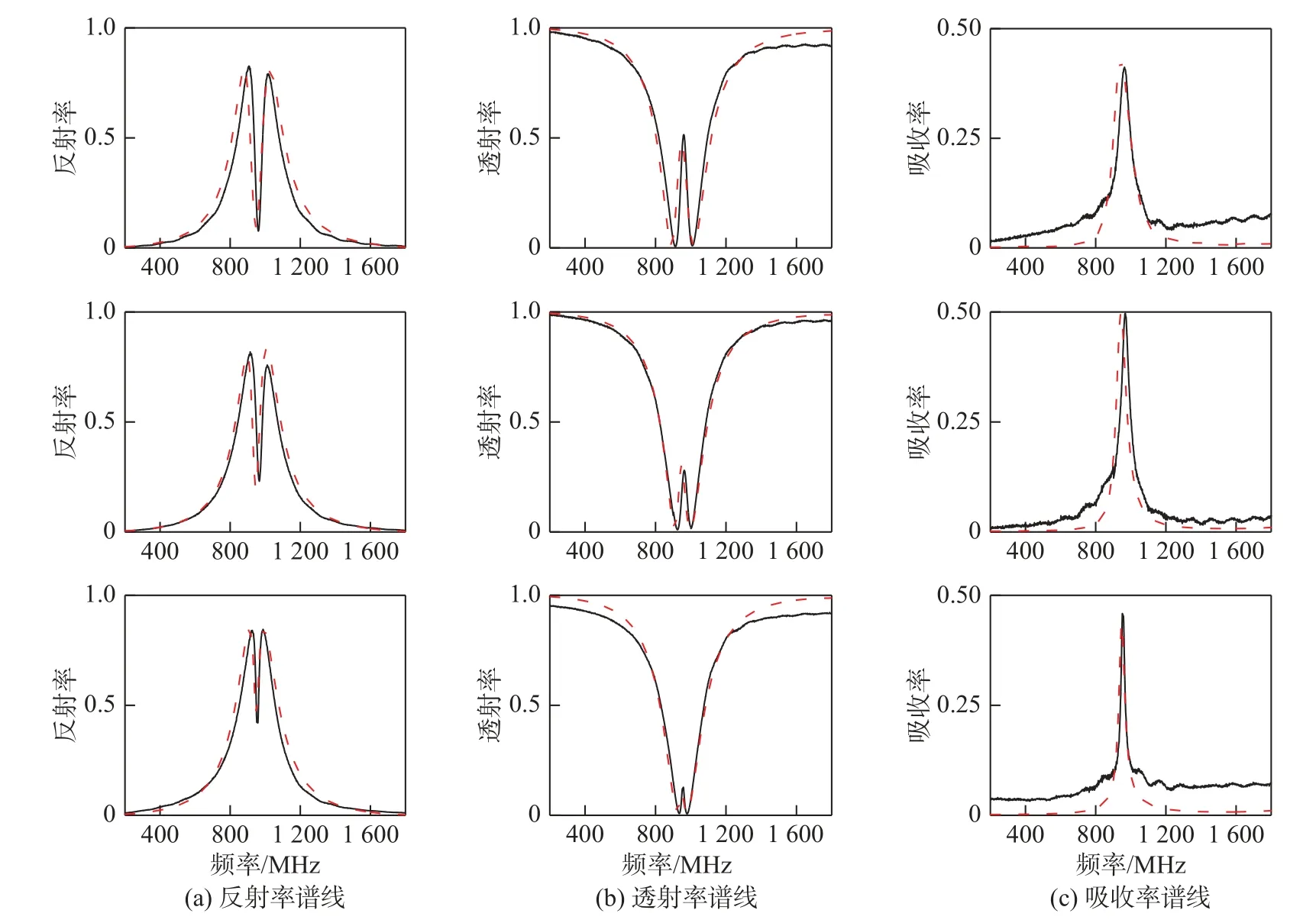
图4 仿真计算（红色虚线）和实验测试（黑色实线）的不同耦合强度下EIT样品的频谱响应Fig.4 Simulations （red dash） and measurements （black solid） of the spectra response of the EIT element at different coupling strength

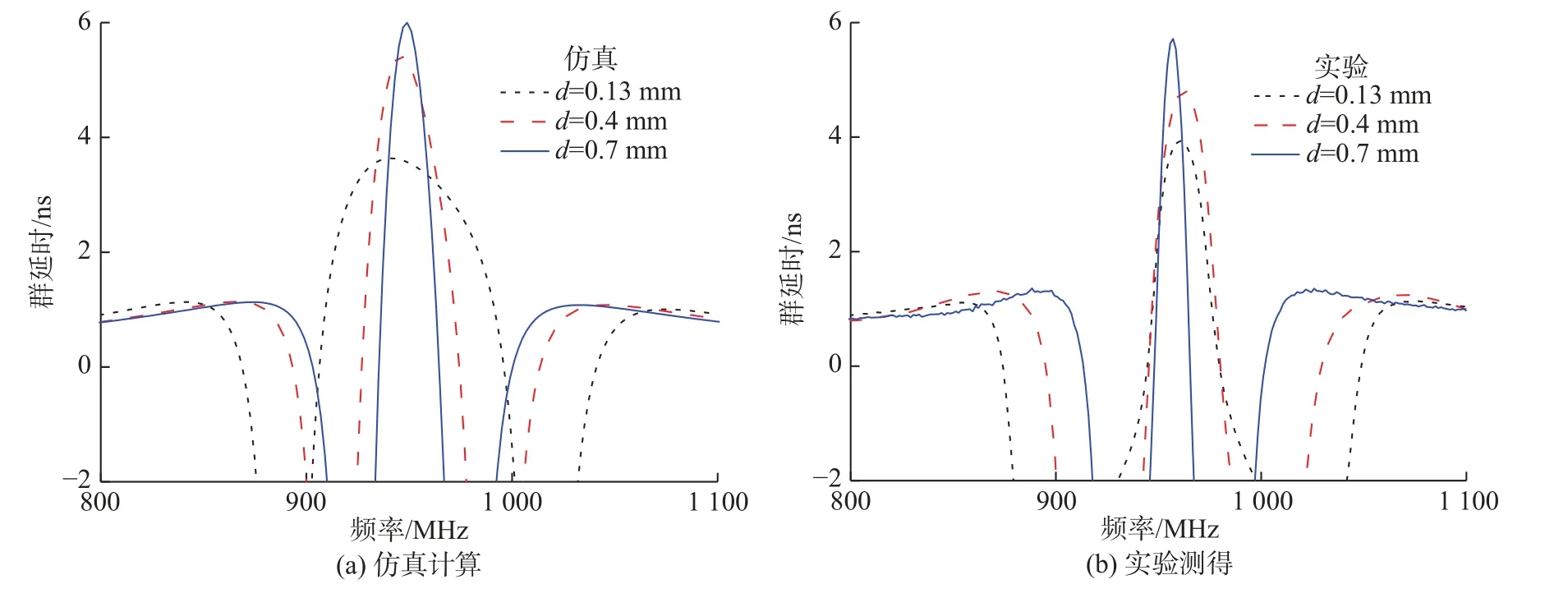
图5 不同耦合强度下的群延迟Fig.5 Group delay of the EIT element at different coupling strength

最后，对3个样品的慢光效应进行了研究，测量了群延迟谱线。测试结果如图5所示。图5（a）为仿真结果，图5（b）为实验结果。黑色短虚线表示的是耦合距离为0.13 mm样品的群延迟谱线。红色长虚线表示的是耦合距离为0.4 mm样品的群延迟谱线。蓝色实线表示的是耦合距离为0.7 mm样品的群延迟谱线。实验结果和仿真结果吻合得很好。从图中可以看出，随着耦合强度的逐渐减弱，EIT透明频率处群延迟由3.7 ns逐渐增大到5.7 ns，慢波带宽逐渐变窄，慢波效应明显。这是因为群延迟和慢波效应与EIT透明窗口的品质因子有关，品质因子越大，慢波效应越明显。

3 结 论

利用梳状线和开口谐振环组成的耦合结构，实现了超构材料中的类电磁感应透明现象。实验研究表明，随着耦合强度的减小，EIT透明频率处的反射率呈逐渐增大趋势，透射率呈逐渐减小的趋势，吸收率呈现先增大后下降的趋势，并利用耦合模理论对整个现象作出解释。同时，通过测试群延时谱线，得到随着耦合强度的减小，EIT透明频率处的群延时逐渐增大，但慢波带宽逐渐变窄。这是因为EIT透明窗口的品质因子变大的关系。整个结构为平面波导型结构，尺寸为深亚波长尺度，便于集成和小型化。研究结果为设计滤波器和慢波功能性器件提供了实验依据。