原子核结合能的协方差分析

2018-11-22王梦茹郭文军郗梓涵张霄吉

上海理工大学学报 2018年5期

王梦茹，郭文军，郗梓涵，张霄吉

（上海理工大学理学院，上海 200093）

原子核质量的精确计算与测量对于核物理以及核天体物理等许多领域的研究具有很高的应用价值，例如，快中子俘获过程（r-过程）中原子核质量起着重要作用[1]。通常考虑原子核核力的饱和性、同位旋对称性等基本性质的核质量模型包括有限力程的小液滴模型（FRDM）[2]、Duflo-Zuke模型[3]、 Hartree-Fock-Bogoliubov（ HFB）模型[4]和Weizsäcker-Skyrme（WS）质量公式[5-7]等，这些模型参数通常由约2 000多个原子核质量的实验数据[8]来确定，由它所预言的原子核质量，精度可以达到0.3～0.6 MeV[7]。基于某个未知原子核的邻近几个已测量核的质量，结合一些几何关系来预言原子核质量的模型有同量异位多重态质量方程（MME）[9]、Garvey-Kelson关系[10]、质子-中子残余相互作用[11]等。

高精度的核质量数据在核结构以及核天体的研究中具有重要的应用。随着科学技术的发展，人们建立了一批批新的放射性束流线和高精度质量谱仪，原子核质量测量成为一个越来越热门的研究领域。Jiang等[12]在计算相邻的原子核的质量时提出了一种新方法，末尾的1个质子和2个中子之间的质子-中子相互作用为V1p-2n,末尾的2个质子和1个中子之间的相互作用为V2p-1n,对于核子数A≥60的核子，通过实验提取相邻的原子核的结合能。使用一个简单的函数来描述V1p-2n和V2p-1n,并能计算出相邻原子核的质量，且提高了计算的精度。Hove等[13]提出了一种新的预测核质量的方法，能用已知的核结合能推出其相邻的核结合能，他们选择4个特定的质量关系构建用来消除核结合能光滑误差的核子数函数，并且通过比较核子相同的奇偶性来消除其快速的奇-偶变化。磁钢度-飞行时间、离子阱、等时性模式质量谱仪、肖特基质量谱仪等方法可以直接测量原子核的质量。偏离β稳定线的奇异核质量的实验数据要比长寿命的稳定核的实验数据少很多[8]。精细核谱学研究小组自2007年以来，利用放射性束流线（RIBLL2）产生的放射性束和冷却储存环（CSRe）等时性模式对67Se等短寿命奇异核的质量进行了直接测量[14-18]。Tu等[19]利用兰州重离子加速器冷却储存环（HIRFL-CSR）装置，首次对100 ms量级的短寿命近质子滴线核素63Ge,65As和67Se的质量进行了测量。在等时性模式下，质量精度达到百万分之一。该项研究得到的65As核素的高精度实验数据解决了核天体物理中的一个重要问题，即对于第一类X射线暴，64Ge不是快质子俘获过程中的一个重要的“等待点”核,消除了X射线暴的一个不确定性。Zhang等[20]精确测量了近质子滴线短寿命核素41Ti，45Cr，49Fe和53Ni的质量，实验精度达到0.02～0.04 MeV。此项研究利用新得到的高精度原子核质量数据，首次在fp壳层对同位旋多重态质量公式（IMME）进行了严格的检验，发现对于质量数A=53，同位旋多重态T=3/2，IMME公式失效。这一现象是现有的核理论无法解释的。该研究发现IMME公式失效，意味着人们对原子核同位旋对称性及其破缺的认识是不完备的。Yan等[21]测量了一系列短寿命T=-3/2核素，包括45Cr，实验精度达到千万分之一。基于取得的实验数据，特别是精确测定的45Cr的质量，确定了X射线暴模型计算在低质量区rp过程核反应路径的走向，否定了理论预言的Ca-Sc循环的存在。

核物质状态方程是核物理研究的热点之一[22-23]。在原子核质量的液滴模型中，对称能项与核物质状态方程紧密相关。而对称核物质状态方程人们己经有了比较清楚的了解，但是，对于非对称的核物质状态方程还不确定，尤其是同位旋相关的部分，即核物质的对称能，人们颇有争议。非对称核物质状态方程的确定能极大地提高原子核质量理论上的计算精度。对称能在重离子反应、核结构、天体核物理等研究中具有重要的影响[24-29]。目前，在一定区域，关于对称能范围的结论产生重叠，达到了初步的共识[30]。但是，不同的模型方法对对称能的约束结果仍然有很大的不确定性。因此，通过实验与模型计算相比较来获取更精确的对称能是当前研究的热点。

Fattoyev利用协方差方法研究了中子皮和中子星[31]，首次给出了理论计算中的参数的误差以及参数和参数之间的关联。本文利用Fattoyev给出的协方差方法，通过对比系数间的关联性、系数和结合能误差的关联系数，合并或优化系数的个数的研究，为得到更为精确的原子核质量提供理论依据。

1 理论模型

自1935年Weizsäcker根据液滴模型给出了半经验的核质量公式，在之后的几十年里，人们对此公式进行了反复的修改，最终得出了较为完整的原子核结合能 EB半经验公式（Weizsäcker公式）：

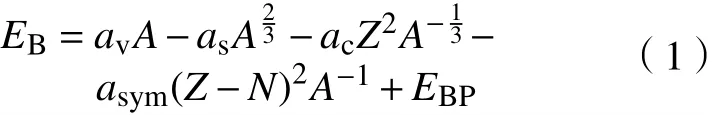
式中：av，as，ac，asym，ap分别为体积能项系数、表面能项系数、库仑能项系数、对称能项系数、对能项系数；A，Z，N分别为原子核的质量数、质子数和中子数；EBP为对能项对于偶偶核、奇A核和奇奇核分别取值

式（1）表示的原子核结合能EB由5项组成，依次为体积能项、表面能项、库仑能项、对称能项、对能项。

图1是文献[8]中给出的2 854个原子核的结合能分布，由图可以看出，原子核的结合能在铁元素附近达到最大，而远离β稳定线核素的结合能迅速下降，整个核素图中的结合能分布呈现环状分布。现将对Weizsäcker公式中的5项系数进行调整，使其能够满足该文献中的实验结果。如表1所示。

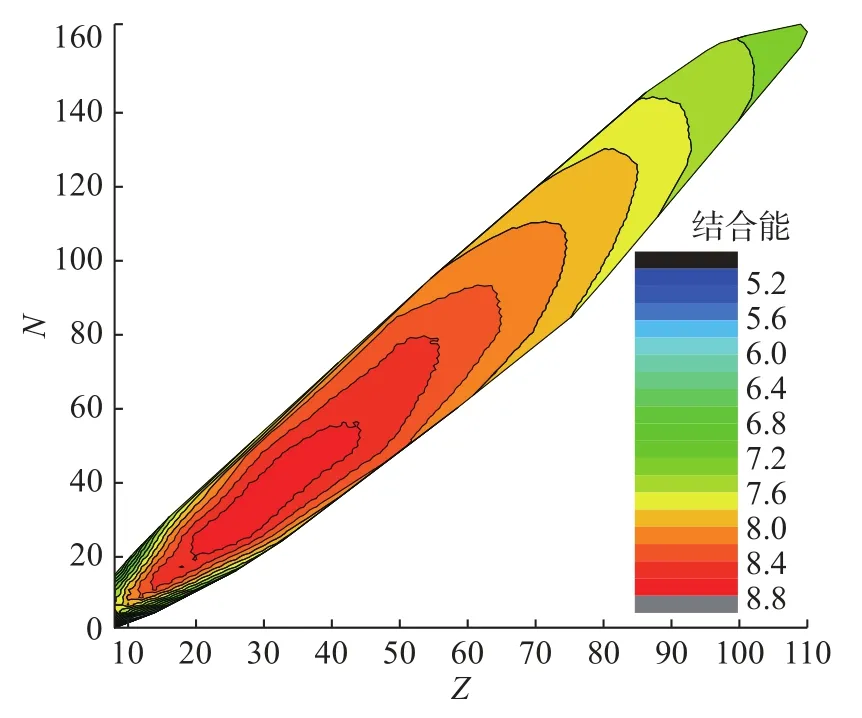
图1 原子核结合能的分布Fig.1 Distribution of the nuclear binding energy

2 结果与讨论

通过最小二乘法计算了文献[8]中的2 854个原子核的结合能，并给出了对应的5个参数。因为，比原有公式考虑了更多的核素，所以，表面能、库仑能、对能的系数改变很多，说明远离稳定线核素的结合能同这3项关系紧密。

表1 Weizsäcker公式原始数据以及本文得出数据Tab.1 Original data of Weizsäcker formula and the data obtained in this article

使用新的参数计算了质子数在8～110之间总计2 854个核素的比结合能百分比误差和绝对误差，并且画出图2和图3。

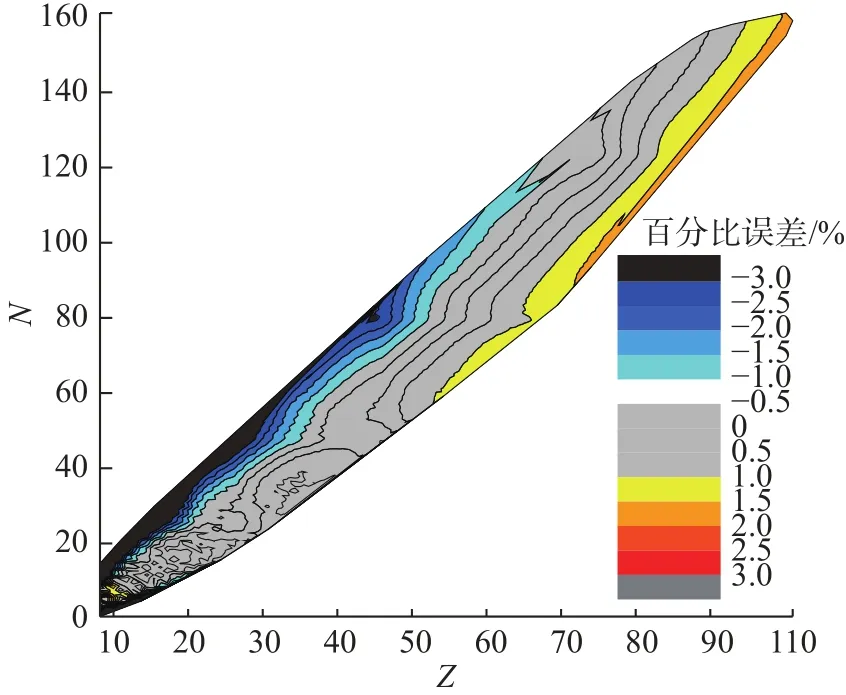
图2 原子核比结合能的百分比误差分布Fig.2 Percentage error distribution of the nuclear ratio binding energy

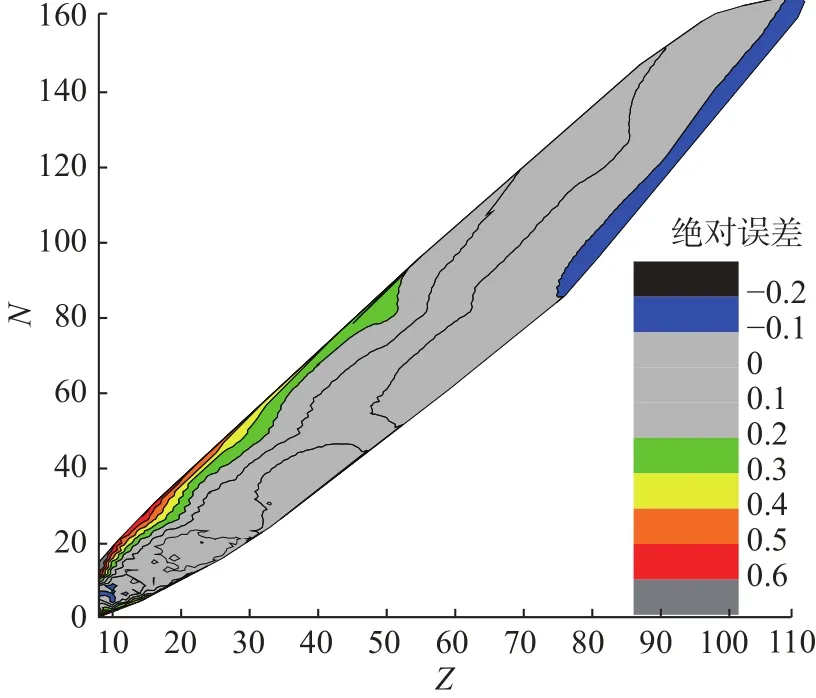
图3 原子核比结合能的绝对误差分布Fig.3 Absolute error distribution of the nuclear ratio binding energy

图2 中灰色的部分表示误差在1%以内，可以看出，在稳定线附近的核素的比结合能误差都较小，而在丰中子区和缺中子区比结合能的误差达到3%左右。图3中灰色部分比结合能的误差在0.1 MeV以内，同样可以看出，稳定线附近核素的误差较小。以上说明远离稳定线的核素可能会有不同的结构，本文将采用协方差的方法找出什么因素导致远离稳定线核素的比结合能误差较大。

为了得出各个系数之间的关系，采用了Fattoyev给出的协方差方法，对系数间的关联系数进行了研究。在原子核中起主导作用的是核力，而核力又有短程性、饱和性、强相互作用等的特点，至今人们无法得到核力的所有性质，增加了原子核结合能的不确定性。传统的描述核特征的模型有小液滴模型和费米气体模型等，Weizsäcker公式是小液滴模型的主要推论，其中体积项占主导作用。从表2给出的各系数间的关联系数中可以看出，体积能项系数与其他4个系数的关联程度较小，说明液滴模型是可以较准确地描述原子核核力的饱和性质的，而核力的饱和性质主要同原子核的体积相关。表面能项与库仑能项关联系数较大，且为负关联，说明两者关系密切，如果原子核为椭球型，则其表面积增大，库仑能减少，呈现负关联。表面能项与对称能项也关联紧密，这同样是因为远离稳定线原子核中中子质子分布的不均匀，会出现中子皮或质子皮现象，造成原子核的实际半径增大。所以，随着原子核远离稳定线，原子核的表面积越来越大，两者呈现正关联。最后，库仑能项也和对称能项紧密相关，库仑相互作用就是重要的同位旋效应，系统的中子质子分布越不均匀，系统的对称能就越大，同时会有很明显的中子皮、质子皮出现，从而造成库仑能计算中的半径与对称能负相关，最终造成两者出现明显的负相关。综上所述，在结合能表达式中，体积能项相对独立，而库仑能项、表面能项、对称能项紧密相关，当原子核存在四极形变或中子（质子）皮时，三者会出现明显的关联。

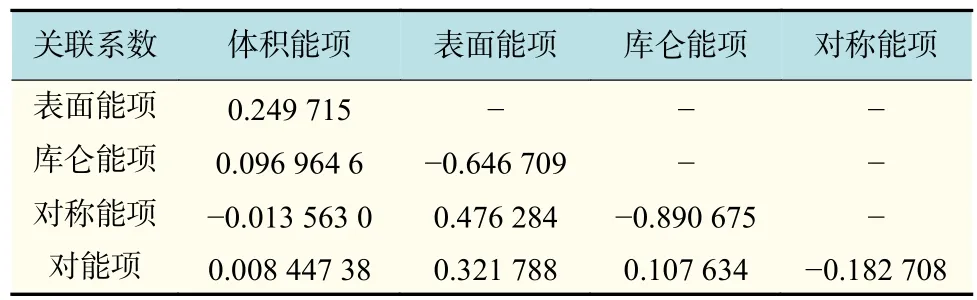
表2 各个系数之间的相关系数Tab.2 Correlation coefficient between various coefficients

表3给出5个系数的误差，从中可以看出，体积能项系数的相对误差最小，仅为千分之一，说明体积能项的表达式较为准确，可以正确描述原子核结合能中的主要部分。而对称能项系数的相对误差较大，也就是说对称能项不能够完全描述体系中的对称能部分，这主要是因为作者对对称能了解的信息还较少。当前核物理中一个主流的研究方向就是研究对称能，在不同核密度情况下，物理学家给出的对称能的数值也千差万别，作者需要更为准确的表达式来描述体系中的对称能部分。表3中对能项系数的相对误差最大,造成这样的原因有待进一步讨论。

表3 各个系数的相对误差Tab.3 Relative error of each coefficient %

表4给出了5个系数与结合能的关联系数。可以看出，体积能项系数与结合能误差的关联系数接近于0，同样说明体积项的表达式较为准确，不需要进一步调整。而表面能项、库仑能项、对称能项对结合能的误差贡献很大，一方面说明这三项作者研究得不够清楚或者是因为忽略掉了四极形变和皮结构等因素；另一方面为作者给出更为精确的结合能公式指明了道路。最后对能项对结合能的误差贡献很小，这可能是因为对能项奇偶相错，其影响被平均掉了，也造成了对能项系数的误差很大。