并发加权μ-演算的一致性内插

余 寒，张晋津

(南京航空航天大学 计算机科学与技术学院，江苏 南京 210016)

0 引 言

在计算机科学领域，μ-演算是一种广泛使用的逻辑[1-3]。命题μ-演算由Kozen[4]提出，通过带不动点算子的公式来表达转移系统[5-7]的性质，是一种表达能力很强的逻辑语言。并发加权μ-演算(concurrent weightedμ-calculus，CWC)，通过将不动点操作符加入并发加权逻辑[8](concurrent weighted logic，CWL)扩充而来，是一种带有不动点的多模态逻辑，能够应对组合性标记加权转移系统(labeled weighted transition system，LWS)。

为了处理CWC上的一致性内插定理，引入二阶量词互模拟。互模拟量词由Andrew M. Pitts提出[9]，随后被用作工具来证明模态逻辑中一致性内插定理，继而延伸到模态μ-演算的一致性内插定理的证明。一致性内插定理能够推出Craig内插[10]，是它的加强版本，可以有效表达模块化。

文中介绍了CWC的语法和语义模型，以及展开的概念，阐述了CWC上的一致性内插定理，引入互模拟量词并证明一致性内插定理在CWC上成立。

1 预备知识

本节给出文中使用的一些符号和基本概念，介绍CWC的语法及LWS语义。

1.1 标记加权转移系统

定义1[8,11](标记加权转移系统)：LWS是一个五元组W=(M,Σ,θ,l,ρ)，其中

(1)M是一个非空的状态集；

(2)Σ是一个非空动作集；

(3)θ:M×(Σ×)→2M是一个状态转移函数；

(4)l:M→是一个满足下列条件的函数：如果m'∈θ(m,a,x)，则l(m')=l(m)+x。一般称函数状态l为标记函数；

(5)ρ:Q→2M是一个关于命题变元集合Q的解释函数。对于p∈Q，N⊆M，解释函数ρ[p|→N]满足下列条件：如果p'=p，则ρ[p|→N](p')=N；如果p'≠p，则ρ[p|→N](p')=ρ(p')。

对于任意LWSW=(M,Σ,θ,l,ρ)，p∈Q，N⊆M，W[p|→N]表示这样的LWS：W[p|→N]=(M,Σ,θ,l,ρ[p|→N])。W-q表示这样的LWS：W-q=(M,Σ,θ,l,ρ-q)，其中ρ-q:Q{q}→2M是一个关于命题变元集合Q{q}的解释函数。定点LWS是一个二元组(W,m)，m是W中的一个状态。

定义2[8,12](加权互模拟)：给定一个LWSW=(M,Σ,θ,l,ρ)，一个加权互模拟是关系R⊆M×M,其中任意(m,m')∈R满足下列条件：

(1)l(m)=l(m')；

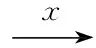
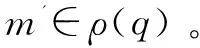
如果存在一个加权互模拟关系R使得(m,m')∈R，则m和m'是互模拟的，记作m～m'。若Wi=(Mi,Σi,θi,li,ρi),mi∈Mi,i=0,1且m0和m1互模拟，则(W0,m0)～(W1,m1)。

将上述条件4改为“对于q∈P⊆Q，m∈ρ(q)当且仅当m'∈ρ(q)”，则对应关系变为P-互模拟，记作～P。

定义3(LWSs乘积)：给定同步函数[13]*:Σ×Σ→Σ,以及任意两个LWS，Wi=(Mi,Σi,θi,li,ρi)，i=0,1。W=(M,Σ,θ,l,ρ)是W0和W1的乘积，记W=W0⊗W1，其中:

(1)M=M0×M1；

(2)Σ=Σ0*Σ1={a0*a1|a0∈Σ0,a1∈Σ1}；

(3)l:M→是满足以下条件的函数：如果(m0,m1)∈M，则l((m0,m1))=l0(m0)+l1(m1)；

(4)θ:M×(Σ×)→2M是满足以下条件的函数：如果(m0,m1)∈M,a∈Σ,x∈,则x=x0+x1,a=a0+a1}；

(5)ρ:Q→2M是满足以下条件的函数：ρ(q)={(m0,m1)∈M|m0∈ρ0(q),m1∈ρ1(q)}。

容易验证W0⊗W1是个LWS。

1.2 并发加权μ-演算

定义4(基本公式)：CWC的公式由以下BNF范式定义，其中r∈{,≥}，

ø::=p|ø∨ø|ø∧øøø|ø|ø|μpø|νpø。

在形如μpø,νpø这样的公式中，要求变量p在ø中正出现(也即，p不出现)。不动点操作符是量词，free(ø)是所有出现在ø中的自由变元的集合。如果ø中的每个命题变元p只被限制一次并且每个p在其限制量词的辖域内，则ø是范式形式。对于范式形式公式ø中的受限变元p，ø的唯一的子公式ηpø(η∈{μ,ν})记作øp。每个公式可以通过重命名受限变元形成等价的范式形式。下文中的CWC公式均指其范式形式。CWC公式在LWS上的解释见图1。

1.3 轮替树自动机

定义5[15-16](轮替树自动机)：轮替树自动机是一个四元组W=(S,s0,δ,Ω),其中:

(1)S是一个有限的状态集合；

(2)s0∈S是一个初始状态；

(3)Ω:S→ω是一个优先级函数；

(4)δ:S→TC是转移函数。集合TC是满足下列条件的最小的集合：如果r∈，则如果q∈Q,则q,q∈TC；如果s∈S，则如果s,s'∈S，则s∧s',s∧s',s|s'∈TC。

图1 CWC的LWS语义解释

轮替树自动机的计算行为用执行(run)的概念来解释。轮替树自动机W=(S,s0,δ,Ω)在(W,m0)上的一次执行是树R=(V,E,λ)，其中(V,E)是定义树的二元组，而λ:V→M×S是一个双标记函数。该树的根节点标记为(m0,s0),带有双标记(m,s)的节点v满足下列条件：

(1)如果δ(s)=q,则m∈ρ(q)；如果δ(s)≠q，则m∉ρ(q)；

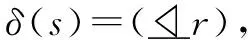
(3)如果δ(s)=s',则存在v'∈Scc(v),使得λ(v')=(m,s')；

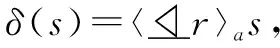
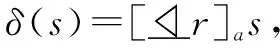
(6)如果δ(s)=s'∨s''，则存在v'∈Scc(v)，使得λ(v')=(m,s')或者λ(v'')=(m,s'')；

(7)如果δ(s)=s'∧s''，则存在v',v''∈Scc(v)，使得λ(v')=(m,s')并且λ(v'')=(m,s'')；

(8)如果δ(s)=s'|s''，存在v',v''∈Scc(v)和m',m''∈M，使λ(v')=(m',s')并且λ(v'')=(m'',s'')。

对于每一个R的无限分支π,将优先级函数Ω应用到每个节点上，对于所得到的自然数序列，当其中无限次出现的最大自然数是偶数，这个分支能够被接收。如果R的每个无限分支是可接收的，则R是可接收的。当一个定点LWS上存在一个关于W可接收的执行，则这个系统是能够被W接收的。

1.4 展 开

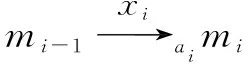
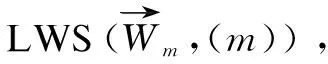
2 CWC上的一致性内插

定义8 (局部后承)：给定两个CWC公式ø和ψ，ψ是ø的局部后承(记作ø|=ψ)，那么对于任意定点LWS(W,m)，如W,m|=ø，则W,m|=ψ。

定义9(一致性插值)：令ø为任意CWC公式，并且O⊆free(ø)。那么ø关于O的一致性插值是满足如下条件的公式θ：

(1)ø|=θ；

(2)如果ø|=ψ并且free(ø)∩free(ψ)⊆O，那么θ|=ψ；free(θ)⊆O。

一致性内插定理在CWC上成立，意味着当适当条件成立时，可以为每个CWC公式找到一个一致性插值。

定理1(一致性内插定理)：任意CWC公式都有一个一致性插值。

证明定理1，需要借助互模拟量词。

3 互模拟量词

互模拟量词在LWS上具有独特的语义，结合互模拟量词和轮替树自动机，可以证明CWC上一致性内插定理成立。

定义10(互模拟量词)：给定一个命题变元q，互模拟量词∃q是具有以下LWS语义的操作符：W,m|=∃qø当且仅当存在定点LWS(W',m')使得(W,m)～q(W',m')并且W',m'|=ø。

其中～q是互模拟关系除去q，即不考虑命题变元q，等价于～Q/{q}。

引理1：给定一个命题变元q，存在映射关系∃q:L→L，使得对于任意CWC公式ø∈L，∃qø满足定义10，并且free(∃qø)=free(ø){q}。

引理1的证明需要借助轮替树自动机。

定义11(轮替树自动机∃qA)：A=(S,s0,δ,Ω)表示一个轮替树自动机，则∃qA是这样一个轮替树自动机∃qA=(S,s0,δ-q,Ω)，其中δ-q:S→TC-q是转移函数，TC-q=TC{q}。

引理2：令A为一个轮替树自动机，那么对于任意定点LWS(W-q,m)，∃qA接收(W-q,m)当且仅当存在定点LWS(W',m'),使得A接收(W',m')并且(W-q,m)～(W',m')-q。

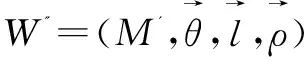
断言1：令(T,τ,t)为一个ω展开树，其中τ:T→W-q并且(T,τ,t)能够被∃qA接收。那么存在映射τ+:T→W,使得τ=(τ+)-q并且A接收(T,τ+,t)。

定理1的证明：固定CWC公式ø和集合O，令q1,…,qn为ø中不在O中的自由变元，也即{q1,…,qn}=free(ø)O。易证∃q1,…,∃qn.ø就是ø关于O的一致性插值。

4 结束语

CWL在模块化系统建模方面效果明显，为了进一步增强CWL的表达能力，提出了CWC。该逻辑系统中包含不动点算子，同时也包括了类似于时态逻辑中的模态操作符和组合模态词。关于Craig内插定理和一致性内插定理，不同的逻辑采用不同的证明方法[17-19]。证明CWC上的一致性内插定理时，引入互模拟量词，再结合LWS上的ω展开和ω展开树，可为CWC中的每个公式找到一致性插值。借助轮替树自动机和互模拟量词，CWC上的一致性内插被证明成立。CWC在表达能力与复杂性之间具有良好的平衡性，在处理很多问题时表现出了一定优势。关于CWC和轮替树自动机，还有更多值得探究的方向，如CWC的模型检测算法，以及轮替树自动机与CWC公理化间的联系等，有待进一步研究。