一种基于Neo4j图数据库的模糊查询研究与实现
2018-11-22李雪
李 雪
(南京航空航天大学 计算机与技术学院,江苏 南京 211106)
0 引 言
在日常生活中,人们想要得到某种结果时,并不能很明确地表达他们的查询要求。例如,寻找一个“高个的年轻人”,其中“高”和“年轻”这样的词语就是模糊的概念。但是一般的数据库管理系统并不能对这样的模糊语句进行查询,因此需要找寻一种有效的方法将模糊的查询条件转化成精确的查询区间,使其可以在数据库管理系统中执行。
随着信息网络技术的飞速发展,各种数据量呈指数级增长,传统的关系数据库无法对这些数据进行很好的处理。为了解决数据量增多以及关系型数据库在处理复杂结构这方面的不足,引入了NoSQL数据库,它被认为是管理大量的图数据或者复杂数据的最佳选择[1]。
众所周知,图通常可以使用一种很自然的方法来表达这个世界[2]。图被应用于许多领域,可以用来表示或存储数据,在不同的场合,图亦拥有很多形式的表示方法或者使用方法[3]。理所当然地,图数据库概念的诞生很快吸引了众多专家学者的关注与研究,它可以有效地管理网络实体中每个节点的特定属性,以及每条边和实体之间的联系[4]。Neo4j是图数据库中比较受欢迎的一种数据库,可以很容易地对关系进行插入删除,在各个领域应用广泛[5]。
国内外对模糊查询进行了大量研究,王青松根据模糊数据自身的各种特性,通过聚类的方法自动生成隶属函数,避免了人为设定隶属函数的主观性[6]。王慧和陈逸菲等不仅对经典关系数据库的查询语言进行了扩展,使其可以处理模糊查询条件,同时还通过对隶属度的计算将权重的概念引入模糊查询,满足了人们查询时各种偏好的设定[7-8]。郑知卉等使用正向法和反向法对查询条件进行处理,将其转化成精确的查询区间[9-10]。
对NoSQL模糊查询研究最多的是A Castelltort等,他们对NoSQL图数据库Neo4j的查询语言Cypher进行扩展,得到Cypherf语言使其可以进行模糊查询,并分别对基于属性、节点和关系的查询语言的扩展进行了研究与介绍[11]。在此基础上,他们还引入了必要的框架来支持NoSQL图形数据库中的近似查询,通过定义和使用Scala,提出Fuzzy4S框架和Cypherf模糊声明性查询语言[11]来定义和运行NoSQL图形数据库的近似查询。其中Fuzzy4S通过领域特定语言(DSL)提供一个框架来定义近似的语言变量。然后,该DSL可以用于查询带有Cypherf的NoSQL图形数据库,该数据库扩展了现有的声明性语言来管理近似查询,该方法将整个链从最终用户的声明性查询级别嵌入到数据库引擎内的实现问题中[12]。
Arnaud Castelltort等还通过对NoSQL图数据库进行扩展,即扩展用于管理带有DSL的不精确查询(定义了灵活的操作符和使用Scala的操作),以及在NoSQL图形数据库中使用Cypherf声明性的灵活查询语言来处理和描述复杂的欺诈行为[13]。他们还提出使用合适的工具用来在Neo4j的Cypher语言中表达模糊查询,用模糊性来帮助解决模糊模式匹配[14]。
BenAli-Sougui I等提出了一个基于图的模糊NoSQL模型,即FNoSQL(Fuzzy NoSQL),用来处理大数据库的同时也扩展了NoSQL[15]。Olivier Pivert等提出了一个可以灵活查询模糊数据库的系统SUGAR,该系统是建立在NoSQL图数据库管理系统中的,支持Cypher查询,由转换模块和分数计算器模块组成,并且引进了Fudge语言来实施,该语言可以灵活地处理模糊的或者精确的数据,可以用来处理模糊图数据库中的偏好查询[16-17]。
1 相关基础知识
1.1 隶属函数
对于论域U∈[0,1]上的模糊集合A,可以表示为:任意一个元素x∈U,都有与其对应的一个隶属函数μA(x)∈[0,1],使得:
(1)
其中,μA(x)表示隶属度x属于模糊集合A的程度。
例如:设论域U=[0,100],模糊集A表示“young”,模糊集B表示“old”,则
(2)
(3)
1.2 α截集
论域U中所有的元素x所对应的隶属函数μA(x)的值都不小于α的一个集合称为模糊集合A的α截集:
Aα={x|μA(x)≥α,∀x∈U,α∈[0,1]}
(4)
其中,α是置信水平(阈值)。
1.3 语气算子
在日常生活中,经常会说“很好”“非常大”“比较容易”等句子,其中“好”、“大”、“容易”等词都是基本单词,用“很”、“非常”、“比较”等词放在它们的前面,对它们的语气程度进行了调整。这种放在基本单词之前,可以对语气程度进行调整的词称为语气算子。
定义1:设Hα为语气算子,HαA=Aα,如果α小于1,称Hα为散漫化算子,如果α大于1,称Hα为集中化算子。其中集中化算子会将原词的影响范围变窄,而散漫化算子正好相反。
假设原词的隶属函数为μ(x),可以有以下规定:
(1)“很”、“非常”等词加上基本词的隶属函数为[μ(x)]2;
(2)“稍微”、“略微”、“有点”等词加上基本词的隶属函数为[μ(x)]0.5;
(3)“极”等词加上基本词的隶属函数为[μ(x)]4。
比如非常老的隶属函数为:
(5)
1.4 模糊化算子
“差不多”、“几乎”、“大约”等词和语气算子不同,它们可以放在原词前,将原词的词义模糊化,这些词统称为模糊化算子。考虑到这些词意思相近,只将“大约”作为标准的模糊化算子。
定义2:可以用一个相似模糊关系μE(x,y),x,y∈U在模糊化算子和被修饰词的隶属函数μ(y)之间作运算,来实现对隶属函数μ(y)的模糊化,记作:
(6)
其中,将δ(δ>0)作为一个参数对模糊范围进行调节,E为相似模糊关系,记为:
(7)
2 模糊查询语言扩展
要在Neo4j图数据库上实现模糊查询,关于模糊性的处理可以基于三方面,分别是基于节点(图数据里面的一个个记录),关系(用来连接节点的一条条边)和属性(也叫作数据的值)。选择一个电影演职员关系图(部分)(见图1)进行介绍。

图1 电影演职员关系
图1显示了在数据库中的演职员和电影的例子,包含了两种节点,分别是导演或者参演电影的演职员,以及上映的电影;其中有“DIRECTED”和“ACTED_IN”这两种关系;关系和节点都通过属性进行具体的描述,其中演职员的属性有:“name”、“born”,电影的属性有:“released”、“title”以及“tagline”。
在此根据电影演职员例子查询“年老的演员出演的2000年左右上映的电影”,其中模糊条件分别是“年老”以及“2000年左右”,将它们分解后逐个进行分析。
2.1 简单条件模糊查询
其中“年老”不是精确的表述,是一种模糊性的概念,但是怎么算是年老?以平时的生活经验可知,50岁以下一般不属于年老,但是50岁以上的人该怎么判断他们哪些是年老的?由式3所定义的关于“年老”的隶属函数可知,50岁及以下可以肯定不是“年老”的人,但是对于50岁以上的人并不能绝对地说他是或者不是年老的人,而是要通过计算隶属函数,得到他们属于年老的“程度”是多少。
进行模糊查询一般根据这样一个过程:用户结合自己的需求输入自己所需的相关条件,根据用户输入的模糊条件找到其中模糊项相对应的隶属函数,根据隶属函数计算所得结果和查询条件进行匹配,看是否满足条件。其中对隶属函数的计算就分为两种方法,即根据文献[9-12]介绍的正向法和反向法实现模糊条件的去模糊化,然后将模糊的查询条件转换成精确的CQL查询,这样就可以在当前的Neo4j数据库中对带有模糊性的条件进行查询。
正向法:需要把所有的模糊性条件都带进相对的隶属函数中,根据隶属函数计算出所有的隶属度,系统会自动生成相应的表来存储这些结果,然后根据题意对隶属度表中的所有隶属度进行求交集或者求并集,得到总的隶属度,将这个隶属度和之前设定好的阈值进行对比,如果匹配度大于或者等于阈值,那么这个条件就是满足的。
在这边,将阈值设定为α,然后将所有条件选项所对应的数值带入隶属函数,计算出每个选项所对应的隶属度,具体的计算过程如下所示:
(8)
对求得的所有隶属度进行求交集或者并集得到总匹配度,具体计算方法如下:
逻辑“AND”的总隶属度计算方法为:
M=min[μ(x1),μ(x2),…,μ(xn)]=min(α1,
α2,…,αn)
(9)
逻辑“OR”的总隶属度计算方法为:
M=max[μ(x1),μ(x2),…,μ(xn)]=max(α1,
α2,…,αn)
(10)
然后将计算出来的总隶属度和原先设定好的阈值α进行比较,如果结果满足M≥α,那么当前的记录是满足要求的;如果结果不满足M≥α,则当前记录不满足条件。
以上方法简单易懂,计算容易,适用于只有少量数据的时候,但是对于要研究的大数据来说计算量尤其复杂,需要扫描数据库中的所有数据,并且计算出这些数据对应的模糊项的隶属度,而且最后还需要自动分配一个表来存储这些结果,表占用了很多的内存空间,会大大降低查询速度,因此更倾向于使用反向法。
反向法:同样也需要事先设定好阈值(α截集),将阈值代入模糊查询条件所对应的隶属函数反向计算得到相应的精确的结果区间,然后用这个精确的结果区间取代原先的模糊查询条件,就可以以常规的方式在Neo4j中实现模糊查询。由于反向法不需要对所有的数据条件进行计算,而是可以根据隶属函数直接进行转换,对于查询庞大数据量时具有很大的优势,而Neo4j是区别于关系数据库的云数据库,里面数据尤其多,所以可以使用反向法进行去模糊化处理。
通过设定的α截集将带有自然语言表述的模糊查询语言转换成精确的查询语句,假设阈值α=0.5,则有如下方程组:
(11)
求解得到的结果为:x∈[55,100]。由此可知,年老的演职员年龄为55到100岁之间。以上成功地将查询“年老”的演职员这一模糊条件转换成了查询年龄在[55,100]这一精确的区间。去模糊化后可以对Cypher查询语言进行扩展来实现这一查询,具体查询语句如下:
查询年老的演职员:
MATCH (p:Person)
WHERE 2017-p.born=OLD(0.5)
RETURN DISTINCT p.name
其中,OLD(α)是将Cypher查询语言扩展后的API,主要为了对是否符合“年老”这一模糊条件进行判断,其中α是阈值,此处设置为0.5。并且由于数据库中并没有直接给出具体的年龄,只是给了每个人的出生年,所以需要用“2017-p.born”进行转换,将它转换成具体的年龄。
2.2 带有语言变量的模糊查询

查询2000年左右上映的电影:
MATCH(m:Movie)
WHEREm.released=GENERAL(0.5,10,2000)
RETURN DISTINCT m.title
对于这个查询语句也使用了一个扩展的API:GENERAL(α,δ,y),其中α是隶属函数的阈值,y是要查询的条件,结果会根据这三个值的改变而进行改变。
以上两个扩展得到了两个查询条件的结果,最后需要查询演员出演的电影,而不仅仅只是将两个扩展的查询条件进行简单的求交集,需要使用(p)-[:ACTED_IN]->(m)语句对它们之间的关系进行限定,然后才能对演职员的关系进行筛选,得到需要的结果。具体扩展的查询语句如下:
复合条件查询:
MATCH(p:Person),(m:Movie),(p)-[:ACTED_IN]->(m)
WHERE 2017-p.born=OLD(0.5) and m.released=GENERAL(0.5,10,2000)
RETURN p.name,m.title
3 系统实现与实验分析
3.1 实验系统
3.1.1 实验环境
文中的原型系统使用Java的Eclipse集成环境开发完成,实现了一个可以在Neo4j数据库进行模糊查询的系统,具体的硬件环境如下:处理器是Intel(R)Core(TM) i5-4590 CPU @ 3.30 GHz 3.30 GHz;8 GB RAM;
界面显示结果所使用的软件环境如下:操作系统是Windows 10专业版64位;具体代码通过Java的Eclipse集成环境编写;数据库使用Neo4j 3.2.6 社区版。
3.1.2 数据集
实验数据采用Neo4j数据库系统自带的“Movie Graph”演职员关系图,主要是数据库中的演职员和电影的例子,包含了两种节点,分别是参演电影的演员或者其他相关的工作人员,以及上映的电影。数据集中所有的关系和节点都通过属性值进行具体的描述,其中演职员“Person”的属性有姓名和出生日期,电影“Movie”的属性有电影名称、上映时间以及电影简介。节点通过关系连接,并且节点通过标签进行说明,其中标签是没有属性的。
在Neo4j图数据库中进行模糊查询实现的原型系统如图2所示。
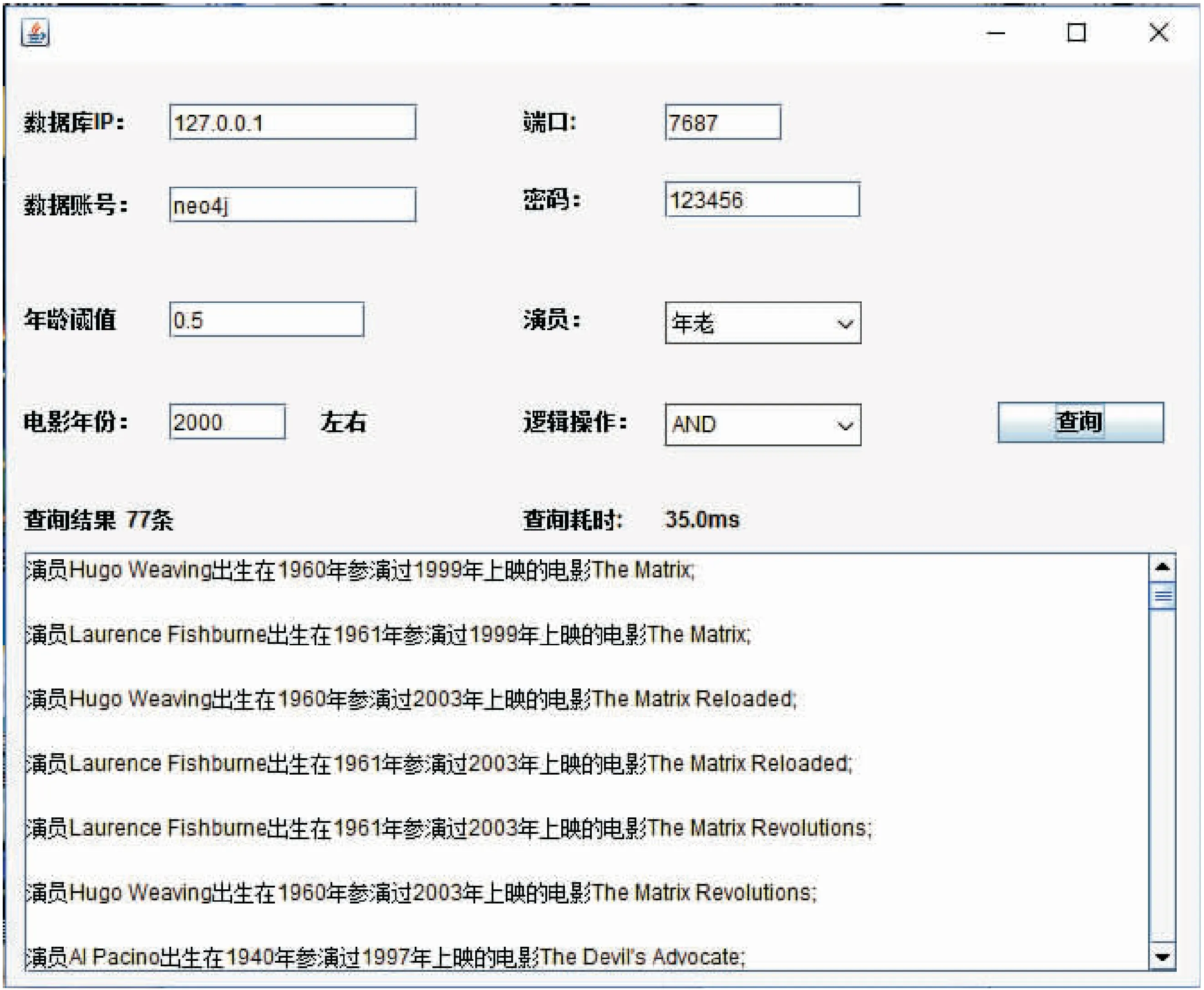
图2 原型系统
3.2 实验分析
基于Neo4j图数据库的模糊查询扩展方法主要是对Cypher查询语言进行扩展,根据隶属函数和α截集相关知识在查询语言上扩展一个API,使用户可以自行输入自己想要查询的条件,通过这个API连接到数据库中,将模糊查询条件经过去模糊化,转换成精确的取值区间,然后在数据库中进行查询,得到所需要的结果。为了验证原型系统的性能,选取不同的查询条件分别在Neo4j数据库和设计的模糊系统中进行查询,对它们的响应时间进行分析比较。
实验分别从常规条件下的查询语句和模糊条件下的查询语句中随机选择4条查询用例进行测试,相应的查询语句如表1所示。
对表1的测试用例分别进行系统响应时间测试。由于系统性能的影响,所有的测试用例都查询十二次,然后去掉最长时间和最短时间,取十次响应时间的平均值进行说明。
从图3可以看出,文中设计的系统的查询响应时间都比数据库本身的要大,但是相差均不超过50 ms,时间差别很小,所以使用模糊系统进行查询是可以接受的。并且从图中可以看出,第三条语句响应时间明显要小一些,是因为它的查询结果很少,只有一条,所以查询结果的数量也是影响响应时间的因素之一。总的来说,图中显示了一般的Cypher查询语言和扩展后的具有模糊性的系统的执行之间没有什么大的区别,在系统中使用模糊语句的额外成本与使用NoSQL图形数据库是一致的。
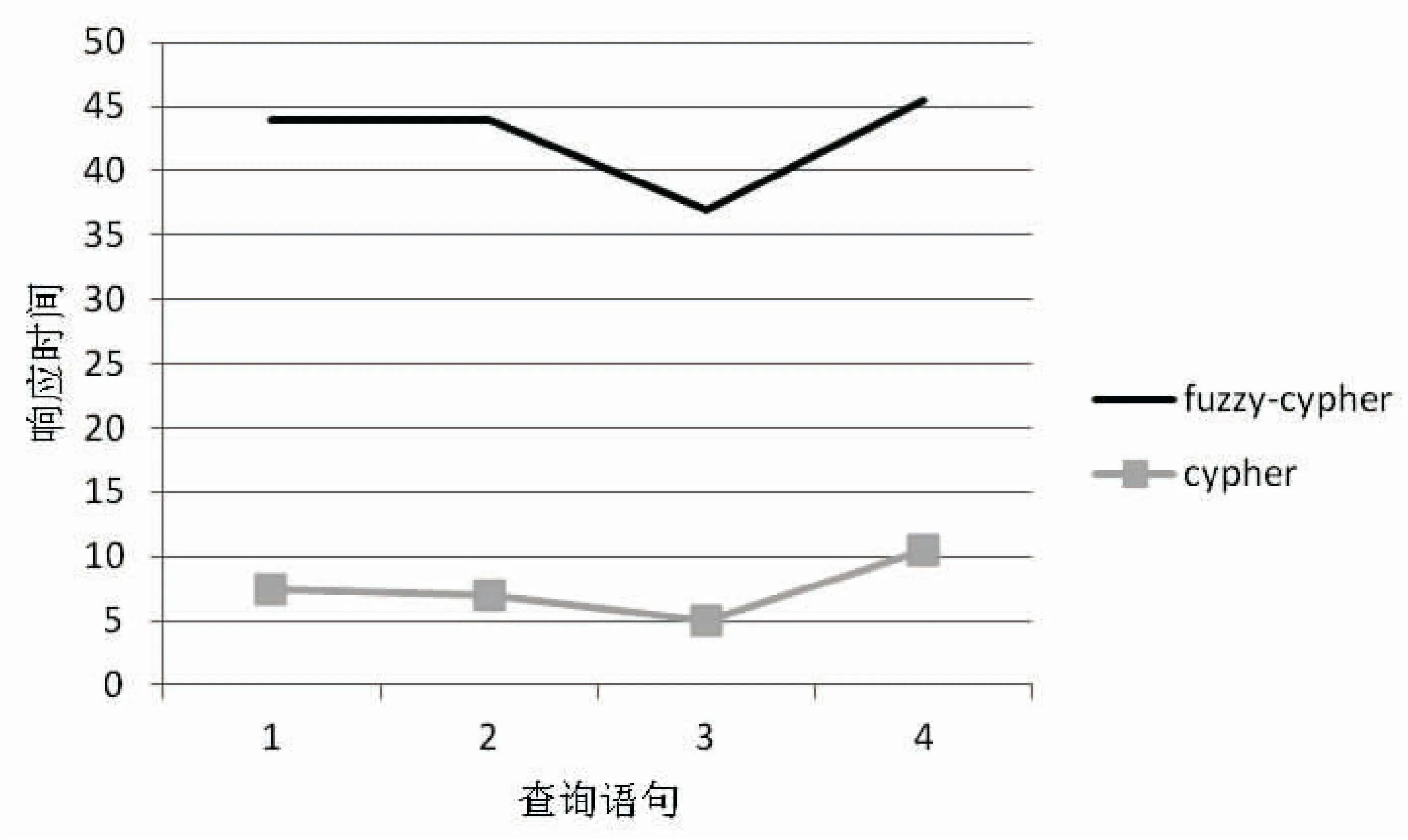
图3 模糊系统和一般查询语言响应时间对比
4 结束语
对Neo4j图数据库的查询语言进行扩展使其可以进行模糊查询,有效解决了现如今大量数据情况下人们想要使用模糊的查询条件查询结果的问题。提出的模糊查询方法主要是对查询语言Cypher进行扩展,将这些扩展在低级API上实现。对于Cypher查询语言扩展方面主要对带有语言变量的模糊查询进行处理,说明了如何将模糊条件去模糊化转换成精确的数值区间进行查询。同时,文中也存在很多不足之处。因为对于不同的模糊集有不同的隶属函数,很难对所有的模糊集都设置一个相对较为准确的隶属函数,而且就算是同一个模糊集,由于所在条件不同,隶属函数的设定也有所区别,所以对该方法实现起来具有很大的工作量,难以运用到实际工程中。目前国内外相关研究还很少,还有很长的路要走。
