光电稳定平台线性自抗扰控制器设计
2018-11-21王春阳彭业光史红伟辛瑞昊
王春阳, 彭业光, 史红伟, 辛瑞昊, 张 硕
(长春理工大学,长春 130022)
0 引言
光电稳定平台是惯性导航、制导及测量系统的核心设备,一般由光电载荷、框架系统、驱动与控制系统等装置构成。其所搭载平台的运动及抖动会造成平台视轴的不稳定,影响其所搭载的光电探测设备的成像质量。光电稳定平台系统内部也存在复杂的干扰因素,如机械谐振、轴系摩擦力矩、传感器噪声等,这些都会对视轴稳定精度造成不利影响。
随着现代技术的发展、目标机动性能的增强,对光电稳定平台要求越来越高,不仅要求其具有更快的响应速度、更好的稳定精度,还要具备抑制大范围扰动的能力。因此,常规的控制策略已难以满足要求,急需寻找新的方法以提高系统的性能。国内外的科技工作者在提高光电稳定平台性能方面对控制策略进行了深入研究。文献[1-2]提出采用高斯型RBF神经网络对摩擦进行观测和补偿的方法;文献[3]针对稳定平台中的非线性扰动,采用LQG和Kalman滤波算法对扰动进行实时估计和补偿;文献[4]采用了基于神经网络的状态观测器并依据完全补偿原理设计陀螺平台控制系统。但是这些方法往往设计难度较大,计算复杂,控制系统成本较高,限制了其在实际工程中的推广和应用。
自抗扰控制技术(Active Disturbance Rejection Control,ADRC)是一种基于“主动抗扰”思想开发的新型实用控制技术,它设计简便,不依赖于系统的数学模型,通过扩张状态观测器分析系统的输入和输出信息来提取系统中的扰动信息[5-6]。线性自抗扰控制技术(Linear ADRC,LADRC)[7]以线性化方式设计各结构,需整定参数较少,十分便于工程应用,已在精密车床中快速刀具系统伺服控制、微机电传感器、航天器姿态控制领域取得了很大成功[8]。文献[9]将线性自抗扰控制技术应用于光电平台稳定回路控制,有效提高系统的稳定精度。
虽然自抗扰控制不依赖被控对象模型的数学模型,但是对于某些系统,可通过一些手段获得被控对象的部分模型信息[10]。将这些模型信息加入到LESO设计中,降低LESO的观测负担,在不提高观测器带宽的情况下提高对扰动的观测精度,提升控制效果,同时避免过多噪声进入系统[11]。
本文以某两轴两框架机载光电稳定平台为研究对象。首先对系统结构做简要说明,通过系统辨识,获得其数学模型,然后开展了基于平台模型的线性自抗扰控制器(Model-based LADRC,MLADRC)设计工作,最后与未采用模型信息的线性自抗扰控制器进行仿真对比,仿真结果表明了该方法的有效性。
1 光电稳定平台结构及模型
1.1 光电稳定平台结构
图1所示的两轴两框架结构的光电稳定平台是目前应用较多且技术较为成熟的一种。该结构是将光电载荷等侦察设备安装在俯仰框架上,陀螺和旋转变压器分别为测速和测角元件。
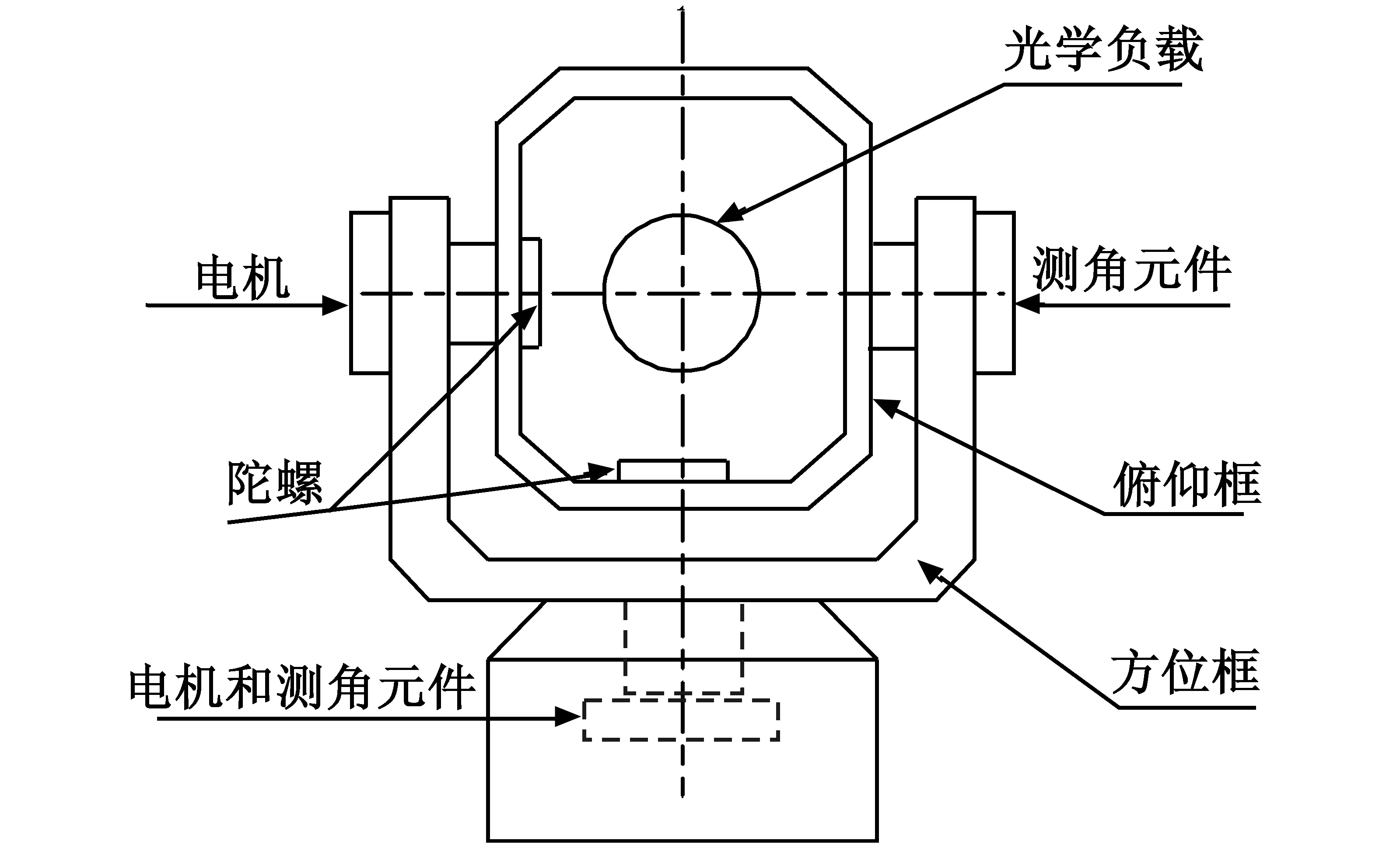
图1 光电稳定平台结构Fig.1 Structure of photoelectric stabilized platform
图2是光电稳定平台单轴稳定回路控制框图。主要结构包括功率放大器、电机及负载、陀螺、旋转变压器和控制器。
光电稳定平台控制系统由速度内环和位置外环构成。外环通过旋转变压器检测转塔当前位置与输入指令的偏差;内环通过陀螺检测空间角速度。二者均对机动平台的载体角运动有隔离作用,但位置环带宽较窄,只能隔离极低频率的扰动,系统中起主要隔离作用的是速度环,且速度环控制通常比位置环更迅速、有效,因此改善速度环动态特性是提升系统性能的关键。
方位轴和俯仰轴互相正交,所以它们之间的耦合作用基本可以忽略,且它们的控制过程基本相同,所以取方位轴的速度环作为控制研究对象。
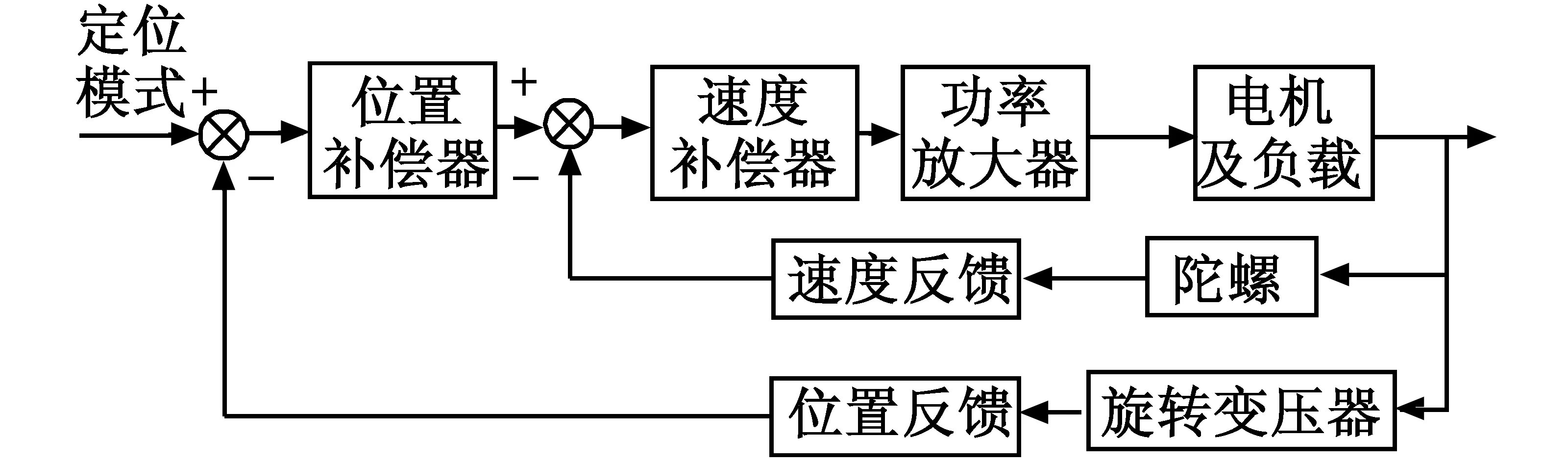
图2 单轴稳定回路控制框图Fig.2 Diagram of a single-axis stabilization loop
1.2 光电稳瞄系统模型
光电稳定平台是包含有很多非线性因素的复杂系统,难以通过机理分析的方法对模型进行准确描述,因此利用系统辨识的方法根据实测的输入输出数据进行模型参数辨识。具体是将正弦扫频信号作为系统输入,求出平台在不同频率段的响应特性,然后通过最小二乘法辨识求取系统的频率特性。平台方位轴频率特性曲线如图3所示。
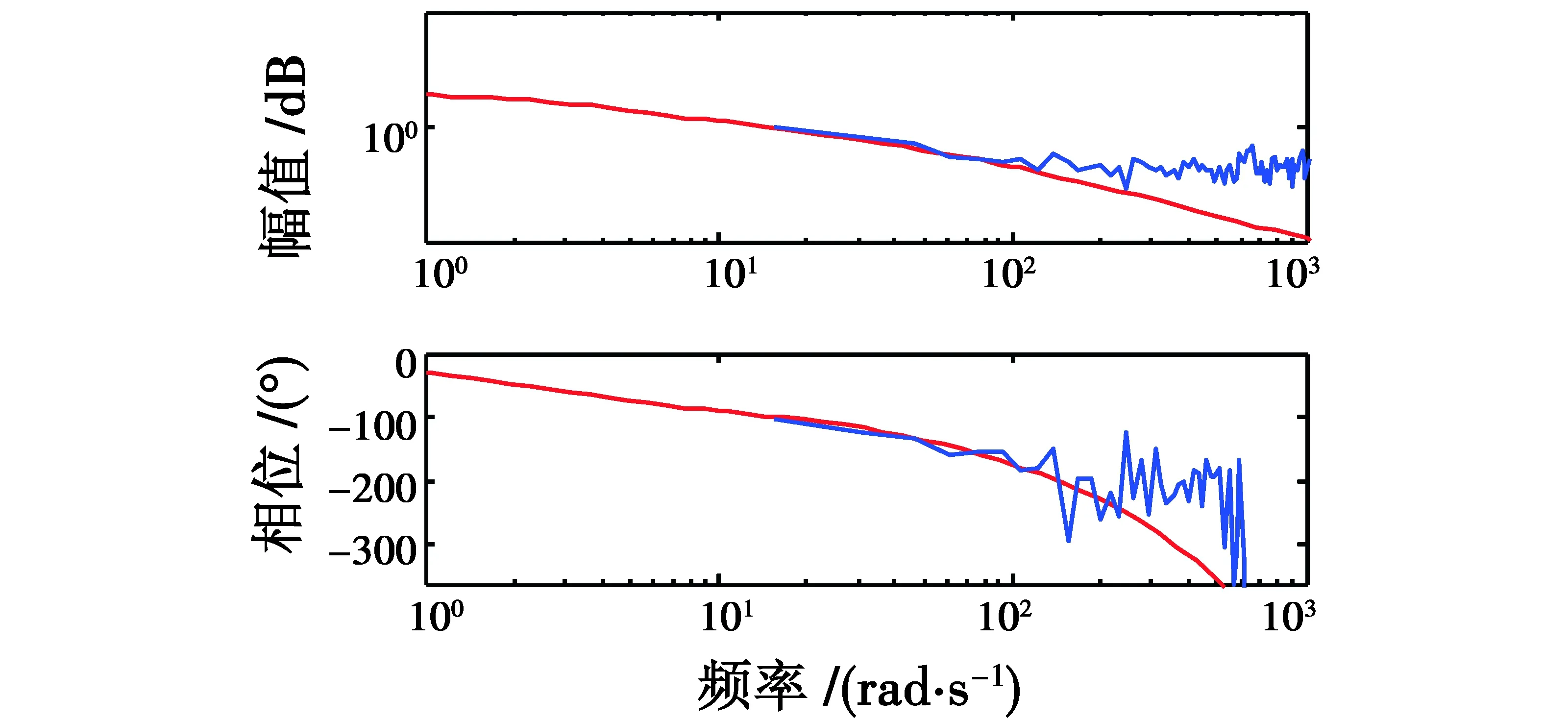
图3 方位轴频率特性曲线Fig.3 Frequency curve of direction axis
通过对频率特性进行拟合和辨识,可得方位轴的传递函数为
(1)
2 基于平台模型的线性自抗扰控制器设计
基于平台模型的线性自抗扰控制器设计包括包含模型信息的线性扩张状态观测器(Model-based LESO,MLESO)设计和PD控制器设计。
2.1 MLESO设计
式(1)的方位轴传递函数写成微分方程的形式为
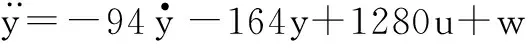
(2)
式中:y和u分别为系统的输出和输入;w为未知的外部扰动,则式(2)又可写成
(3)
式中,b0为输入增益的近似估计,为可调参数。
(4)
其连续状态空间描述为
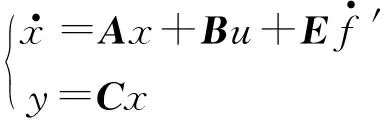
(5)

将扰动f′扩展为系统的状态变量x3=f′,则可得包含模型信息时式(3)系统的扩张状态方程为
(6)
通过比较A,B,E,C和A′,B′,E′,C′可发现,主要区别在于状态矩阵A′和输入矩阵B′包含了更多被控对象的信息。
根据式(6)建立基于平台模型设计的MLESO,表达式为
(7)
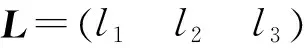
根据文献[7]中的方法,选取扩张状态观测器的误差增益为
(8)
式中,ωo为观测器带宽,扩张状态观测器的调整仅需改变ωo的值,其值越大,扩张观测器对各个状态的跟踪速度越快,跟踪误差越小,但高带宽会增加系统对噪声的敏感度,导致过多噪声进入系统。同时,实际中ωo受系统硬件性能和采样步长的影响,不可能任意大,往往需要在跟踪精度和噪声抑制能力上做出妥协。
2.2 PD控制器设计
经过MLESO对扰动的估计和补偿,采用PD控制器即可对系统进行很好的控制,控制器为
u=(u0-z3)/b0
(9)
式中:u0=kP(v-z1)-kDz2。
系统闭环传递函数为
Gcl=kP/(s2+kDs+kP)
>。
(10)

(11)
式中,ωc为控制器的带宽,PD控制器的调整仅需改变ωc的值,它决定系统的响应速度,其值越大,系统响应越快。但是,带宽过高会引入传感器的高频噪声,而且还会引起机械谐振。
从上文设计过程中可看出,基于平台模型信息的线性自抗扰控制器与未采用模型信息的线性自抗扰控制器的不同之处在于扩张状态观测器的设计是否加入了被控对象的模型信息。MLADRC控制器最终需要调整的参数仅为ωo,ωc和b0,参数整定方便,便于工程应用。
3 仿真与结果分析
在Matlab/Simulink 中进行未采用模型信息的LADRC与采用模型信息的MLADRC仿真对比。在观测器带宽和控制器带宽、增益相同的条件下进行阶跃响应、角速度扰动抑制、力矩扰动抑制的对比,结果如图4所示。
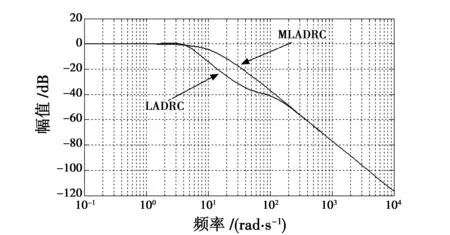
图4 伯德图Fig.4 Bode plot
从图4可以看出,在观测器带宽ωo、控制器带宽ωc、增益b0相同的条件下,加入模型信息后,闭环系统获得的带宽更大,也就意味着系统响应速度更快。
3.1 阶跃响应
加入幅值为1 rad/s的阶跃信号作为输入信号,从图5中可看出,采用MLADRC控制器,系统阶跃响应不仅没有超调,而且进入稳态的时间更短,显示了MLADRC较好的动态响应特性。
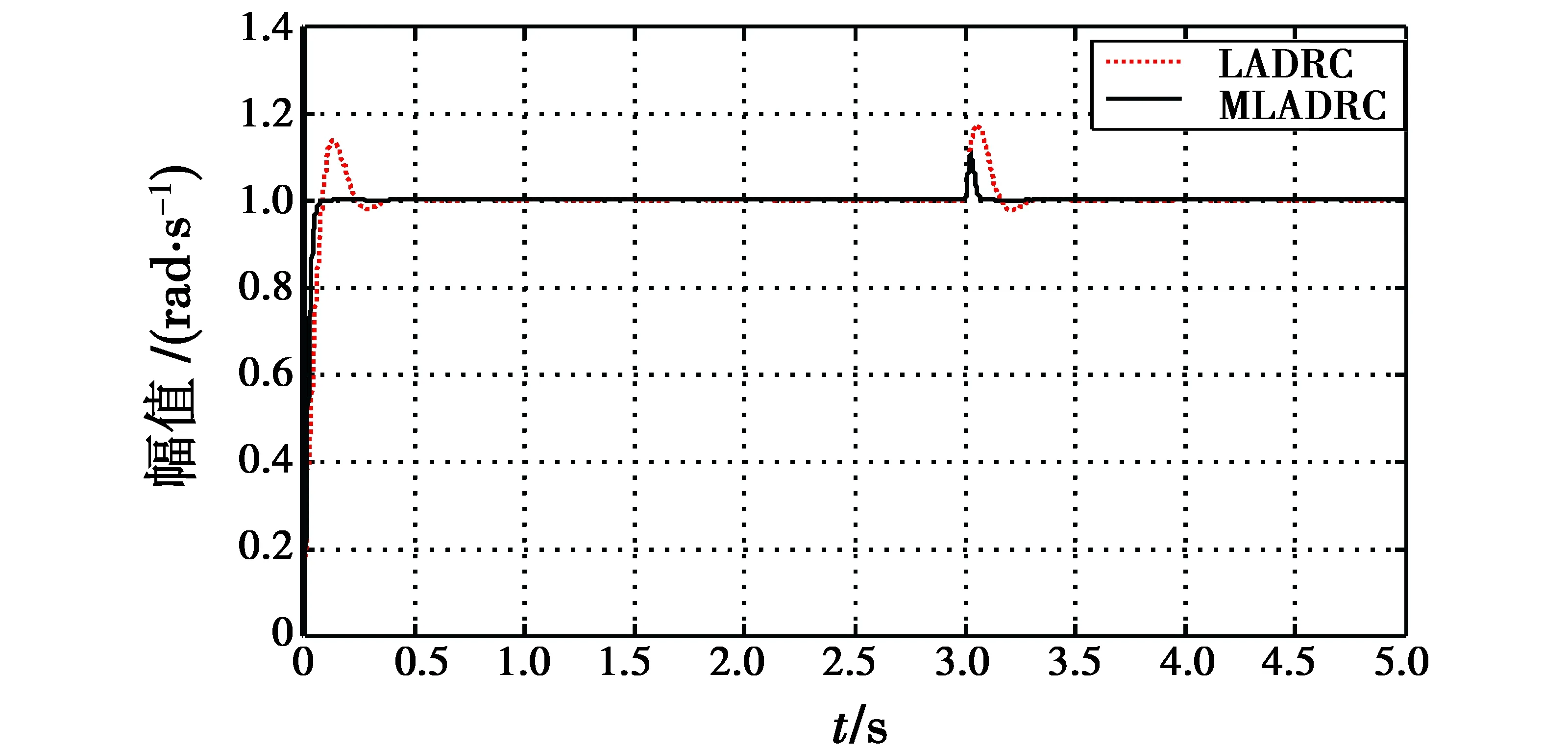
图5 阶跃响应Fig.5 Step response
输入端第3 s加入幅值为1 rad/s的阶跃信号作为扰动信号。扰动对MLADRC控制下的系统造成影响较小,且MLADRC消除扰动的速度更快,体现了较强的鲁棒性。
3.2 扰动抑制能力分析
LADRC和MLADRC的不同之处是观测器内部结构不同,其他各处结构均相同。图6 为LADRC/MLADRC的控制器结构框图,以及平台扰动所加位置。
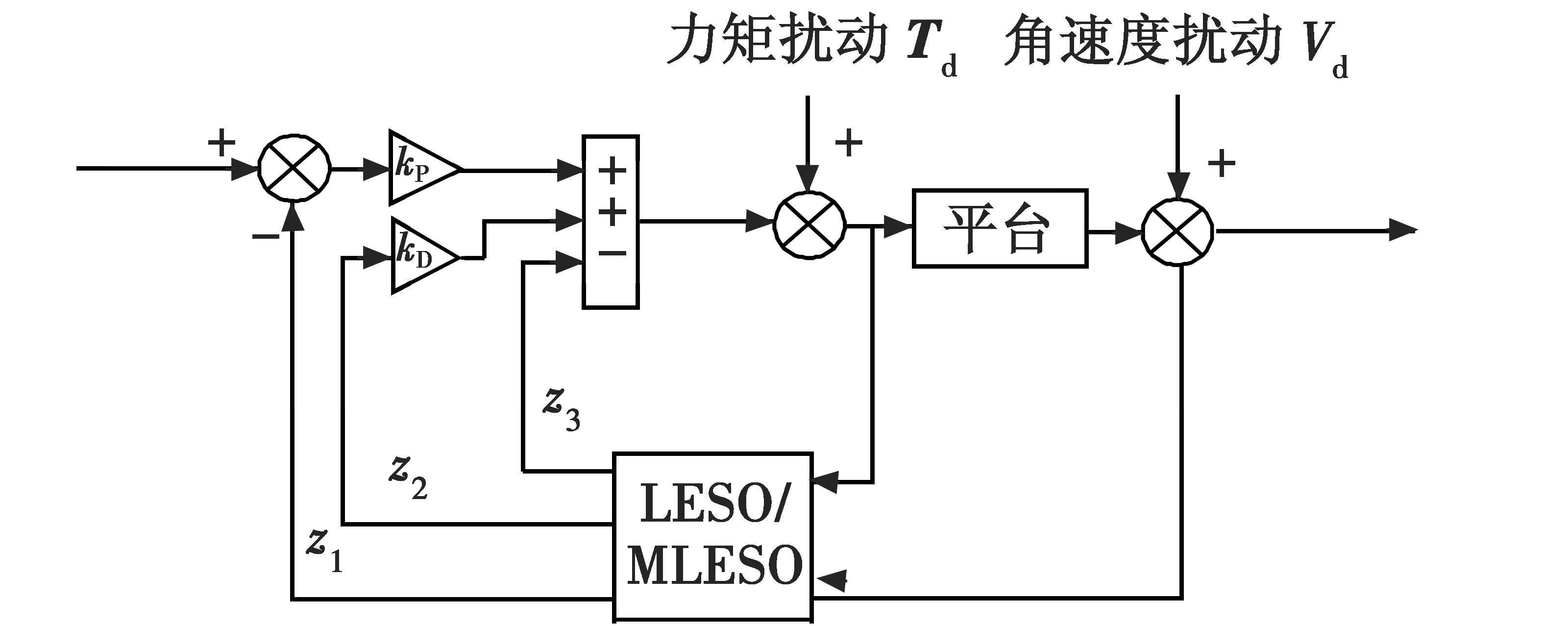
图6 LADRC/MLADRC控制框图Fig.6 Diagram of LADRC/MLADRC
分别加入平台力矩扰动Td和平台载体角速度扰动Vd,参考信号为0,进行MLADRC和LADRC的扰动抑制能力对比。所加扰动分别为:力矩扰动Td是幅值为1 N·m、频率为1 Hz的正弦信号;角速度扰动Vd是幅值为3 (°)/s、频率为1 Hz的正弦信号。
图7和图8分别是在相同观测器带宽、控制器带宽和增益下,系统分别在LADRC和MLADRC控制下的力矩扰动残余和角速度扰动残余。

图7 力矩扰动残余Fig.7 Residue of torque disturbance
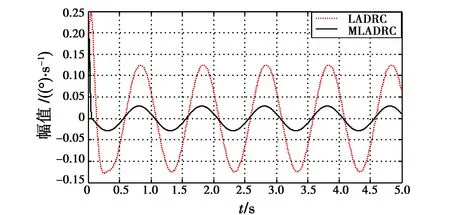
图8 角速度扰动残余Fig.8 Residue of velocity disturbance
表1为在不同观测器带宽和不同控制器带宽下LADRC和MLADRC控制下系统扰动残余均方值。

表1 扰动残余均方值
从表1中可看出,采用模型信息的MLARC具有更好的扰动抑制能力,随着观测器带宽和控制带宽的增加,扰动抑制能力逐渐増强。
4 结束语
仿真分析结果表明本文提出的利用平台模型信息进行光电稳定平台线性自抗扰控制器设计的方法可有效提高系统的响应速度和扰动抑制能力;基于模型信息设计的MLADRC需要整定的参数仅为3个。同时,该方法也可应用于其他能够获取对象模型信息的相关系统,具有一定的工程应用价值。
