改善MIMO-STAP检测性能的收发联合优化方法

乔惠娇， 王洪雁， 裴炳南

(大连大学辽宁省北斗高精度位置服务技术工程实验室，辽宁 大连 116622)

0 引言

近年来，随着多输入多输出(Multi-Input Multi-Output,MIMO)通信的蓬勃发展，以及雷达为突破自身限制对新理论、新技术的需求，MIMO雷达概念应运而生[1]。与只能发射相干波形的相控阵雷达相比，MIMO雷达可利用多个发射单元发射几乎任意波形。按照天线距离的不同，MIMO雷达可分为分布式MIMO雷达和集中式MIMO雷达[2]。分布式MIMO雷达相邻阵元间有较大间距，可从不同角度对目标进行检测，从而可利用空间分集提高目标检测性能[3-4]；相反地，集中式MIMO雷达相邻接收阵元之间间距较近，因此只能从某个角度对目标进行观测，以获得更多系统自由度，进而可改善角度分辨力、参数辨识能力、参数估计精度，以及干扰抑制性能[5]。

MIMO雷达研究领域中，波形优化一直是非常活跃的方向之一。MIMO雷达波形优化问题通常可归纳为如下两种类型：只考虑发射端波形优化，以及联合优化发射波形及接收权。FRIEDIANDER首先通过设计发射波形以最大化输出信干噪比(SINR)进而改善MIMO雷达检测性能[6]。然而，其基于梯度算法求解所得优化问题，不能保证SINR在每次迭代中不减，进而不能确保收敛。针对此问题，CHEN提出一种接收权及发射波形联合优化的迭代算法，所提算法可保证迭代中每一步不减，进而可确保迭代收敛[7]。

为了提高MIMO雷达检测性能，众多基于空时自适应处理(Space-Time Adaptive Processing,STAP)技术的MIMO雷达检测算法相继被提出[8-9]。STAP技术具有同时抑制杂波和干扰的特性，既可实现与复杂外界环境的有效匹配，又可在一定程度上补偿系统误差造成的影响，因而可显著改善雷达系统性能[10]。基于此，WANG等深入研究了MIMO-STAP杂波秩与发射波形的关系，并给出确定杂波秩的准则[11];此外，WANG等通过设计发射波形以改善MIMO-STAP检测性能[12];然而，上述文献仅考虑通过优化发射端以改善MIMO-STAP检测性能。众所周知，在传统相控阵系统中可通过设计接收权改善STAP检测性能[13];因此，可以综合发射波形及接收权的优势以改善MIMO-STAP检测性能，文献[14-15]只讨论了理想环境下发射波形和接收权联合优化问题，而未同时考虑抑制杂波、降低旁瓣等问题。

针对上述问题，本文考虑通过联合优化发射波形及接收权值以改善MIMO-STAP检测性能。可以证明，高斯噪声条件下最大化检测概率等价于最大化输出SINR[16]。因此，基于最大化输出SINR准则，本文在发射波形恒模特性、抑制杂波及降低旁瓣等约束下构建发射波形及接收权联合优化问题以最大化输出SINR进而改善MIMO-STAP检测性能。为求解所得复杂非线性问题，本文提出一种基于迭代的方法以交替优化发射波形及接收权。需要注意的是，所提方法中的每一步都可转化为半定规划(SDP)问题，从而可以获得高效求解。

1 问题提出

MIMO-STAP雷达可建模如下：收发阵列均是均匀线阵，接收阵元和发射阵元个数分别为N和M，收发间距分别为dR和dT，且均平行分布。雷达平台沿收发阵列方向匀速直线飞行，且脉冲间隔为T。在此场景下，本节将首先分别对目标、杂波及噪声进行建模。

考虑目标信号模型。记发射信号矩阵为S=(s1>s2>…>sM)T，其中，sm∈CK×1表示第m个发射单元的波形样本，K为样本数，则第l个脉冲下的目标接收信号可表示为[17]

Yl=αtej 2 π fD labTS

(1)

式中：fD=2(vsinθt+vt)T/λ为目标多普勒频率,v和vt分别表示该雷达站和目标相对于MIMO雷达的速度；αt和θt分别表示目标信号的复振幅和位置；a=(1ej 2π fs…ej2 π(N-1)fs)T为目标接收导向矢量;b=(1ej 2 π γ fs…ej 2π(M-1)γ fs)T为目标发射导向矢量,γ=dT/dR,fs=dR·sinθt/λ为目标空间频率,λ为载波波长。

基于矢量化公式vec(ABC)=(CT⊗A)vec(B)，且若x，y为向量，则vec(xyT)=y⊗x，可得目标信号矢量化输出为

yl=αtej 2π fDl(ST⊗IN)(b⊗a)

(2)

式中：yl=vec(Yl)；⊗表示Kronecker积；IN表示N×N单位矩阵。

χt=αtd⊗(ST⊗IN)(b⊗a)

(3)

式中,d=(1ej 2 π fD>…ej 2 π(L-1) fD)T为目标多普勒导向矢量。

根据Kronecker积性质(A⊗B)(C⊗D)=(AC)⊗(BD)，式(3)可改写为

χt=α0(IL⊗ST⊗IN)(d⊗b⊗a)=α0Xut(θt)

(4)

式中：X=IL⊗ST⊗IN;ut(θt)=d⊗b⊗a为目标空时频导向矢量。

在接收端需要对接收信号进行滤波处理以得到目标检测充分统计量。则基于式(4)，可得滤波器输出为

Υ=αtwHXut(θt)

(5)

式中,w∈CNKL×1为滤波系数。

由式(5)可知，目标信号输出功率可表示为

(6)

与目标信号类似，本文考虑系统接收杂波信号建模，杂波可建模为NC个杂波块的叠加，则L个CPI脉冲条件下杂波可表示为[18]

(7)

式中：αc和θc分别表示杂波信号的复振幅和位置;uc(θc)=dc⊗bc⊗ac为杂波空时频导向矢量;ac=(1ej 2 π fs,c…ej 2 π(N-1)fs,c)T为杂波接收导向矢量，bc=(1ej 2 π γ fs,c…ej 2 π(M-1) γ fs,c)T为杂波发射导向矢量，fs,c=dRsinθc/λ为杂波空间频率，dc=(1ej 2 π fD,c…ej 2 π(L-1) fD,c)T为杂波多普勒导向矢量,fD,c=2vTsinθc/λ为杂波多普勒频率；Γ(l)∈CLKN×LKN为杂波延迟矩阵[18]。

类似地，接收端对杂波进行滤波处理可得

(8)

式中,w∈CNKL×1为滤波系数。

由式(8)可知，位于θc的杂波输出功率为

(9)

下面考虑系统噪声建模，噪声可建模为高斯白噪声[16]，则L个CPI脉冲条件下的噪声可表示为

z=(vecT(Z1)>vecT(Z2)>…>vecT(ZL))T

(10)

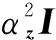
可以证明，高斯噪声条件下最大化检测概率等价于最大化输出SINR[16]。则基于上述目标、杂波及噪声模型，MIMO-STAP输出SINR可表示为[19]

(11)

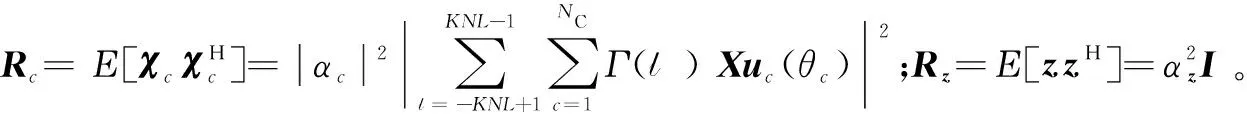
工程实际中，雷达射频放大器通常工作在过饱和状态,使得发射波形呈现恒模特性从而避免非线性效应[20]。恒模约束为：将波形S每个元素模数约束为常数，通常可通过相位编码实现，即

(12)

式中,φi表示发射波形s(i)的相位。

需要注意的是，实际应用中，为改善系统检测性能，不仅要考虑降低杂波功率，还需考虑旁瓣抑制问题[21]。若旁瓣较高，会掩盖附近弱小目标，从而造成检测概率下降。因此，本文需要通过收发联合设计将旁瓣与杂波均限定在给定阈值内。

基于以上讨论可知，在恒模约束、旁瓣及杂波抑制条件下，最大化输出SINR以提高MIMO-STAP检测概率的发射波形及接收权值联合优化问题可表示为[22]

(13)

式中：Θc为杂波范围；Θs为旁瓣范围；μ和σ分别为旁瓣水平和杂波水平阈值。

由于发射波形S为恒模约束，因而上述联合优化问题为NP问题[23]。此问题难以利用凸优化等传统优化方法求解，如若采用基于梯度的方法，则收敛性不能保证。

2 所提迭代算法

为求解式(13)的复杂非线性联合优化问题，本文将采用迭代算法对S和w进行交替优化，即首先固定S以求解w；其次，固定w以求解S。首先考虑固定S求解w，则仅考虑接收权设计的优化问题可表示为

(14)

>。

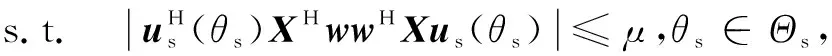
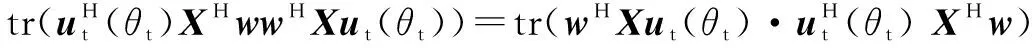
(15)

s.t.wHQtw≤t1;wHQsw≤μ,θs∈Θs,
wHQcw≤σ,θc∈Θc

>。

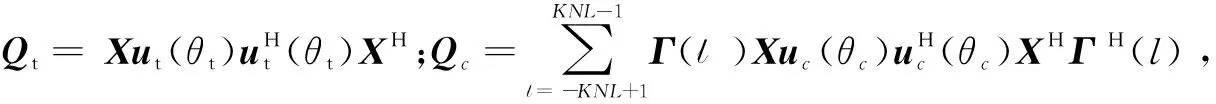
考虑固定w以求解S的波形设计问题。基于式(15)求得接收权条件下，波形设计问题可表示为

(16)

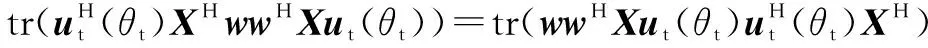
(17)

由Kronecker积矢量化性质：vec(A⊗B)=(Im⊗Kqp⊗In)(vec(A)⊗vec(B))，Kqp为置换矩阵，A∈Rp×m，B∈Rn×q，可得

>vec(X)=vec(IL⊗ST⊗IN)=(IL⊗KMN×L⊗IKN)·

>(vec(IL)⊗vec(ST⊗IN))=(IL⊗KMN×L⊗IKN)·

(vec(IL)⊗IM⊗KN×K⊗IN)(vec(ST)⊗vec(IN))=gJ

(18)

式中：g=(IL⊗KMN×L⊗IKN)(vec(IL)⊗IM⊗KN×K⊗IN);J=(vec(ST)⊗vec(IN))。

基于式(18)，式(17)可重新表示为

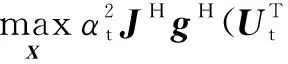
(19)

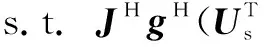
由(A⊗B)(C⊗D)=(AC)⊗(BD)及tr(AB)=tr(BA)可知，式(19)可松弛为如下SDP问题[24]，即

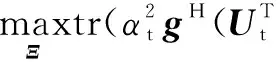
(20)

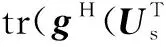
式中：Λ=vec(IN)vecH(IN);Ξ=vec(ST)vecH(ST)。式(15)、式(20)的SDP问题可通过凸优化工具包(比如CVX[25])实现高效求解。

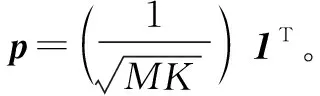
由上述分析可得最优发射波形ST的矢量化形式，即

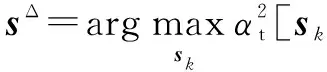
(21)

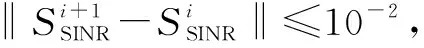
3 数值仿真与分析

(22)

式中：k=1,…,M;n=1,…,K。

图1给出了SNR为-10 dB，CNR为30 dB条件下所提算法得到的最优发射方向图。从图1可看出，所提算法在目标θt=0°处放置了一高峰，表明所提算法得到的优化波形可将发射功率集中于目标位置，从而可提高目标检测概率。此外，可看到图1b中有栅瓣出现，这是由于MIMO雷达(1.5,0.5)发射阵元稀疏布置引起的。

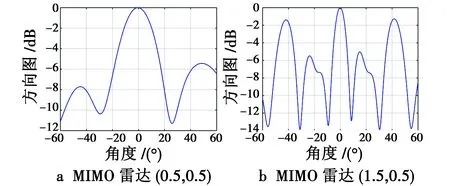
图1 SNR为-10 dB、CNR为30 dB条件下所提算法得到的最优发射方向图Fig.1 Optimal transmission beampatterns obtained by the pro-posed algorithm with SNR as -10 dB and CNR as 30 dB

图2为所提算法、仅考虑旁瓣抑制的算法以及发射不相关波形所得到的输出SINR随SNR或者CNR的变化曲线。从图2可看出，3种方法得到的输出SINR均随SNR的增加而增加，随CNR的增加而降低。然而，需要注意的是，无论SNR或CNR为何值，仅考虑旁瓣抑制方法输出的SINR均高于不相关波形，表明仅考虑旁瓣抑制方法可以改善系统检测概率，且所提算法输出的SINR明显高于旁瓣抑制算法，进一步表明所提算法可以明显提高系统检测性能。此外，由图2可知，雷达(1.5,0.5)输出的SINR略大于雷达(0.5,0.5),这可归因于雷达(1.5,0.5)形成的虚拟孔径大于雷达(0.5,0.5)，因此其可获得更大的分集增益。

图2 所提算法、旁瓣抑制以及发射不相关波形得到的输出SINR随SNR和CNR的变化曲线Fig.2 The output SINR of three methods vs SNR and CNR

图3为所提算法、仅考虑杂波抑制以及发射不相关波形所得到的输出SINR随SNR或者CNR的变化曲线。

图3 所提算法、杂波抑制以及发射不相关波形得到的输出SINR随SNR和CNR的变化曲线Fig.3 The output SINR of three methods vs SNR and CNR

由图3可知，3种方法得到的输出SINR均随着SNR的增加而增加，随着CNR的增加而降低，且相对于杂波抑制及不相关波形，无论SNR或CNR为何值，所提算法得到的输出SINR均优于杂波抑制及不相关波形。图3表明，与仅考虑杂波抑制以及不相关波形相比，所提算法可以显著提高系统的检测性能。此外，由图3可得与图2类似结论，即雷达(1.5,0.5)的输出SINR略大于雷达(0.5,0.5)。

为验证所提算法的收敛性，图4给出了SNR为-20 dB、CNR为30 dB条件下所提算法得到的输出SINR随迭代次数变化的曲线图。从图4可看出，随着迭代次数增加，所提算法得到的输出SINR波动逐渐变小，且无论哪种雷达配置，皆仅需6步左右迭代就趋于稳定，表明所提算法具有较好的收敛性。需要注意的是，由图4还可得到与图2、图3类似结论：雷达(1.5,0.5)得到的输出SINR略高于雷达(0.5,0.5)。

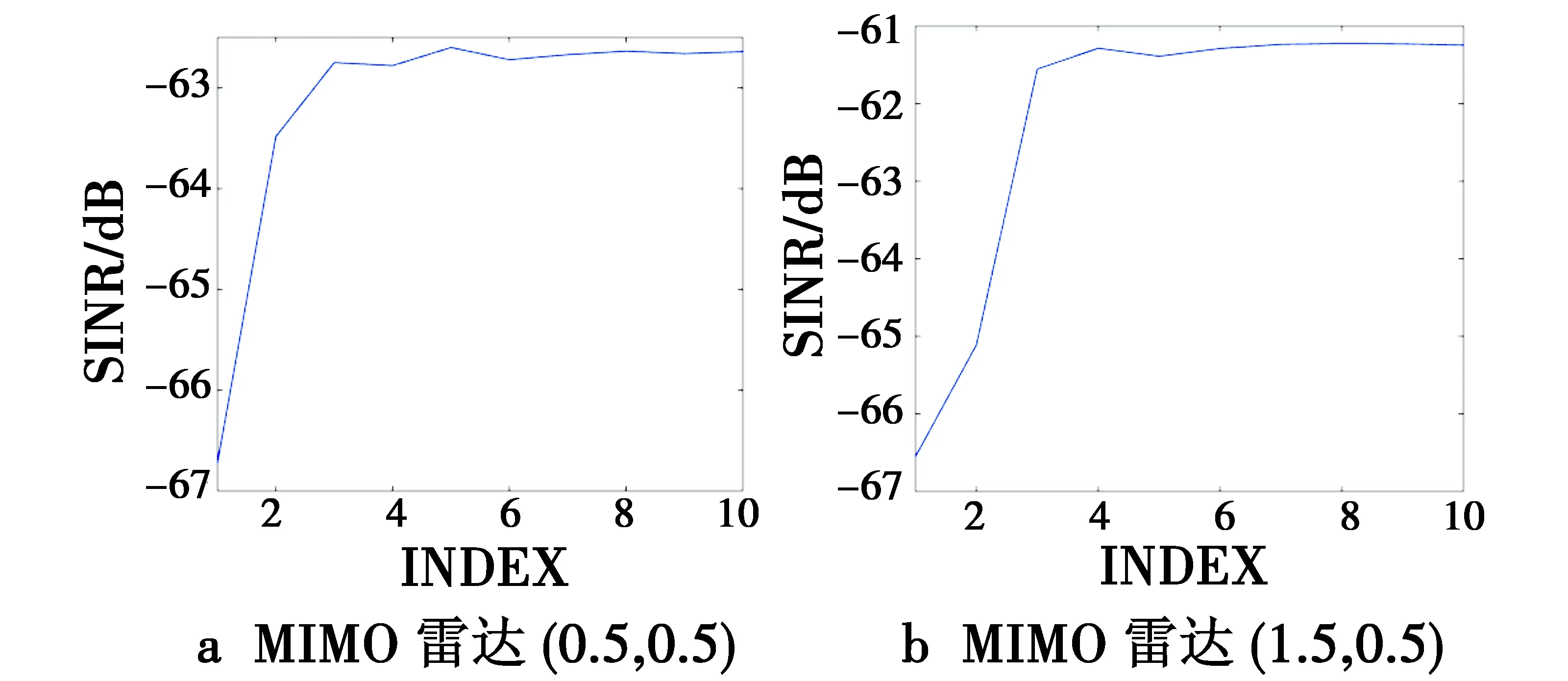
图4 SNR为-20 dB，CNR为30 dB条件下所提算法得到的输出SINR随迭代次数变化曲线图Fig.4 The output SINR obtained by the proposed algorithm vs the iteration numbers with SNR as -20 dB and CNR as 30 dB

4 结束语

本文研究了复杂环境下提高MIMO-STAP雷达系统检测概率的发射波形及接收权值联合优化问题。首先建立了MIMO-STAP系统模型，并基于最大化输出SINR准则，在发射波形恒模特性、抑制杂波以及降低旁瓣等约束下构建发射波形及接收权联合优化问题以最大化输出SINR从而改善MIMO-STAP检测性能。为求解所得复杂非线性问题，本文提出一种发射波形和接收权值联合交替优化的迭代算法，所提算法中每一步都可转化为SDP问题，因而可获得高效求解，且保证了算法的收敛性；数值仿真表明，与仅考虑杂波抑制、旁瓣抑制算法以及不相关波形相比，所提算法可显著改善MIMO雷达的检测性能。