基于正则化参数自适应估计的运动目标提取
2018-11-21杨瑞锋
杨瑞锋, 黄 山
(四川大学电气信息学院,成都 610065)
0 引言
图像作为人类感知世界的视觉基础,是人类获取信息、表达信息和传递信息的重要手段。随着计算机视觉和图像处理在各个领域内的广泛应用,运动目标检测[1]成为当今研究的热点。近些年来,基于稀疏表示的压缩感知理论发展使稀疏表示成为一种有效的数据表示方式。低秩矩阵恢复(RPCA)[1]已经成为一种流行的数据获取和表示方式,随着文献[2]提出矩阵RPCA,开始通过引入稀疏表示从而提高对含有大噪声和异常点的观测数据的鲁棒性。然而随着现代视频数据的数据结构维度增高和更为复杂,为了更好地表达高阶数据复杂的本质结构,文献[3]提出张量高阶奇异值分解,将矩阵的奇异值分解扩展到张量,为高维数据的分析和处理提供有力的支撑。因此,越来越多的研究人员运用张量高阶奇异值分解来实现运动目标提取。但是对实验正则化参数的调试过程是一项工作量大并且耗时长的工程,研究者们开始关注于正则化参数的自适应估计。现有选择参数的方法有Morozov’s 偏差准则[4]、广义交互验证法(Generalized Cross-Validation,GCV)[5]、Curve法[6]和变分贝叶斯法(Variational Bayes’ Approach)[7]等。文献[8]中利用Morozov’s 偏差准则实现了基于全变分的图像去模糊的正则化参数自适应估计,受此启发,本文将采用Morozov’s偏差准则实现基于HOSVD的运动目标检测的正则化参数自适应估计。
1 Morozov’s偏差准则
以图像恢复为例引入Morozov’s偏差准则。一般而言,图像的退化过程可以表示为
V=KUclean+N
(1)
式中:V为观测图像;K为已知的模糊算子的矩阵表示形式;Uclean为原始图像;N为高斯白噪声。根据V估计出Uclean是一个不适定逆问题。用正则化方法求解该问题的最小化方程,即
(2)
式中:J(U)为正则项,U为Uclean的估计值;二次项被称作数据保真项;λ为正则项参数,平衡了保真项和正则项的相对权重。
根据偏差准则,上述问题的解应该存在于集合中
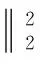
(3)
式中,c=τmnσ2,τ是一个提前确定的参数,mn表示图像的大小,σ2表示噪声方差。当噪声方差σ2未知时,文献[9]提出可以通过中值估计方法(Median Absolute Deviation,MAD)估计出σ2。该方法的理论基础是噪声小波系数主要集中在高频子带中,因此可以通过高频子带系数近似估计噪声系数。另外,中值操作的原因是避免高频子带中存在极少数的大幅度系数对方差估计[10]造成影响。MAD噪声水平估计方法的数学表示为[11]
σ=1.482 6MAD(real(YHH))
(4)
式中:MAD( · )表示求中值;real( · )表示求实部;YHH表示图像经二维小波分解后得到的最高频子带的系数。
在偏差准则下,式(2)问题等价于有约束的优化问题,即
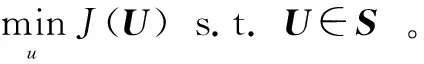
(5)
通过拉格朗日定理可以将式(5)有约束问题转化为式(2)无约束问题。如果U是特定的λ下式(5)的解,那么它也是式(2)的解,用U*(λ)表示式(2)对应的最优解。那么,作为式(5)的最小化,有:U*(0)∈S,λ=0或者
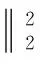
2 基于正则化参数自适应估计和HOSVD的运动目标提取
2.1 张量高阶奇异值分解
张量又称为多阶阵列,是向量和矩阵的高阶推广。其中,零维张量为标量,一维张量为向量,二维张量为矩阵,N阶张量表示为A∈RI1×I2×…×IN,其中元素(i1,i2,…,iN)表示为ai1,i2,…,iN。张量也能够用矩阵形式表示,该过程称为张量的n-模式展开,是将张量的元素重新排列成矩阵。
张量A与矩阵U∈RJn×In的n-模式积是一个维度为I1×I2×…In-1×Jn×In+1×…×IN的张量,用A×nU表示,其元素为
(6)
通常需要求核张量S,可通过下式求得
S=A×1(U(1))T×2(U(2))T×…×N(U(N))T
(7)
式中:S∈RJ1×J2×…×JN为奇异值分解后得到的核心张量,矩阵U(n)∈RIn×In为将张量A的n-模式展开矩阵A(n)进行SVD分解得到的左酉矩阵,符号×n表示张量与矩阵的n-模式积[12]。
2.2 基于正则化参数自适应估计和HOSVD的运动目标提取
将输入的I3帧大小为I1×I2×3的RGB图像序列均转化为I3帧大小为I1×I2的灰度图序列,观测图像序列表示为三阶张量O∈RI1×I2×I3。恢复张量表示的背景部分可由如下凸优化问题形式表示,即
(8)
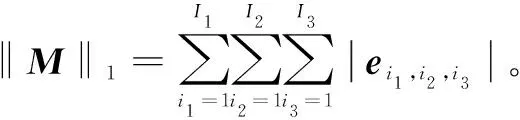
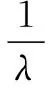
(9)
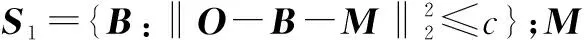
引入辅助变量A=B,则将上式转化为如下问题,即
(10)
s.t.>A=B>。
根据拉格朗日定理,上述有约束优化问题的拉格朗日函数为
(11)
式中:Y1是拉格朗日乘子;β1是正的惩罚参数。本文采用ADMM来求解上述问题,采用偏差准则,推导出参数λ和μ的更新公式,每一次迭代中,随其他变量的更新,参数λ和μ也会按照固定的规律不断更新,直到算法终止。将上述问题分解为以下几个子问题求解,每次迭代中固定其他变量只更新一个变量,迭代步骤如下。
1) 固定其他变量,更新变量A。
(12)
对奇异值阈值收缩进行张量扩展,通过如下3个步骤求得式(12)的最优解。
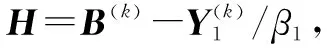
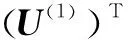
>;
(13)
② 对S进行软阈值收缩;
③ 张量重建
(14)
2) 更新变量B和μ。
(15)
对式(15)右边B求导,令求导后的式子为0,可得
(16)
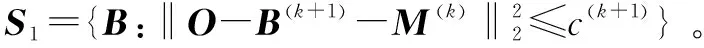
c(k+1)=τI1I2I3(σ(k+1))2
>。
(17)
根据上文可得
(18)
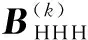
如果
(19)
B*(0)∈S1,μ=0,即
(20)
如果
(21)
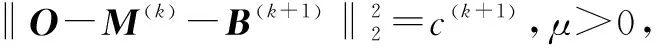
(22)
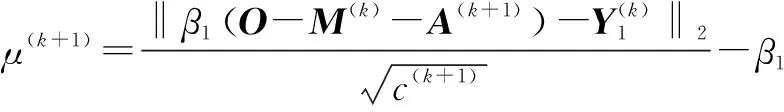
(23)
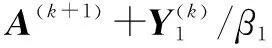
更新变量M,这里引入辅助变量E=M,即
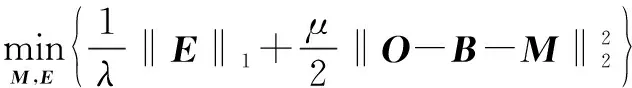
(24)
s.t.>E=M
>。
根据拉格朗日定理,上述有约束优化问题的拉格朗日函数为
(25)
式中:Y2是拉格朗日乘子;β2是正的惩罚参数。
3) 更新变量E。
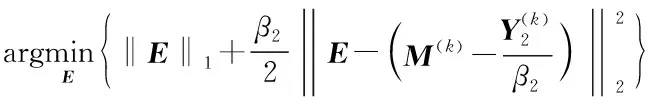
(26)
可通过软阈值收缩算子Sα(Z)求得最优解
(27)
4) 同步骤2),更新变量M和λ。
(28)
(29)
6) 判断终止条件。
(30)
若式(30)满足或者达到最大迭代次数,则终止迭代。
7) 输出表示背景的B(k+1)、表示运动目标的M(k+1);最后对输出的运动目标部分M进行二值化处理,得运动目标G为
(31)
然后进一步对G进行形态学中开闭运算,消除运动目标区域外的噪声,填充目标区域内的空洞,最终提取较准确的运动目标。
3 实验结果及分析
3.1 实验结果
本文数据是从标准的change detection video database (http://www.changedetection.net)数据库中选取4组真实视频序列进行测试,在相同实验环境下,本文方法与近期极具竞争力的鲁棒性主成分分析法(RPCA),以及基于迭代张量高阶奇异值分解(HOSVD)的运动目标提取方法进行比较。
视频1的图片像素大小为180×120。实验选取80帧进行测试,结果如图1 所示。




图1 视频1运动目标检测结果Fig.1 Moving target test results of Video 1
视频2的像素大小为240×140。实验中选取80 帧进行测试,结果如图2 所示。




图2 视频2运动目标检测结果Fig.2 Moving target test results of Video 2
视频3的像素大小为160×120。实验选取80 帧进行测试,结果如图3 所示。




图3 视频3运动目标检测结果Fig.3 Moving target test results of Video 3
视频4的像素大小为160×120。实验选取80帧进行测试,结果如图4 所示。




图4 视频4运动目标检测结果Fig.4 Moving target test results of Video 4
从实验结果可以看出,本文方法在多种场景下比RPCA的提取效果要好很多,与HOSVD方法结果差别不大,能较准确完整地提取运动目标。
3.2 量化对比及结果分析
为量化评估算法提取运动目标的性能,本文采用召回率(Rrecall)、准确率(PPrecision)和两者的调和平均值F-Measure来衡量运动目标检测效果的好坏,即
(32)
(33)
F-Measure能够有效地维持Rrecall,PPrecision这两个标准的平衡,依此评价标准,F-Measure的大小和目标检测的效果成正比,即F-Measure值越高,目标检测的效果越好。
分别计算各视频序列的Rrecall,PPrecision和F-Measure,从表1结果可以看出,本文方法的Rrecall,PPrecision和F-Measure都比RPCA方法高。实验结果证明本文方法提取运动目标更为准确,且能在不需要进行繁琐的手动调试参数的情况下,取得和HOSVD方法几乎相同甚至更好的效果。
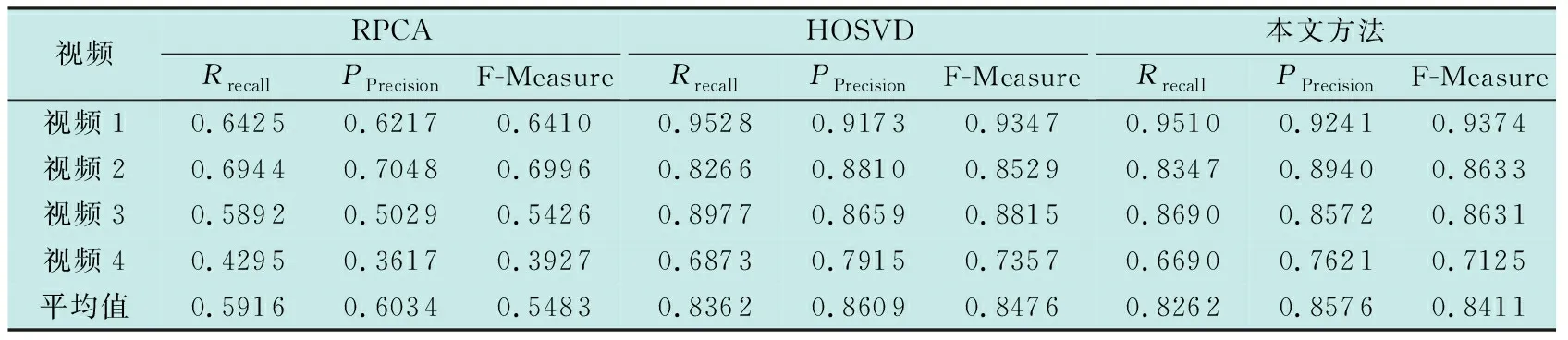
表1 各个视频在不同算法下的结果指标
图5展示了8组图像序列基于常规的HOSVD运动目标检测[14]的F-Measure指标随正则化参数λ变化的曲线图。对于不同的图像序列,它们对应的最优参数都不同,而且这8条曲线都很陡峭,说明λ变化很快,F-Measure值对λ比较敏感;从变化范围看:对于8个图像序列,尽管λ的变化范围都很小,在0~0.04之间,F-Measure的值变化却很大,变化范围从最小值0到最大值1。

图5 F-Measure随λ变化曲线图Fig.5 The changing of F-Measure with λ
综合上述实验数据可知:1) 常规的HOSVD运动目标检测效果的好坏对正则化参数的变化极其敏感;2) 针对不同的实验数据,正则化参数的最优值都不同。由于这两个原因,通过试错法手动调试正则化参数是一件极其困难的事,需要通过大量的实验才能找到最优参数,而本文方法能在不需要进行繁琐的手动调试参数的情况下,取得和HOSVD方法几乎相同甚至更好的效果。
正则化参数不需要设置初值,算法中上限c是已知的与噪声相关的数,本文采用c=τI1I2I3σ2来估计c。τ=1是一个经验值,当τ=2时,目标检测效果最佳且该算法对惩罚参数β1和β2的值不敏感,当它们的取值在较大范围内变动时,实验结果变化不明显,这里选择β1=β2=3×10-3。
4 结束语
本文提出了一种基于正则化参数自适应估计和HOSVD的运动目标提取方法。以Morozov’s偏差准则为理论基础,根据误差水平对正则化参数进行选择和调整。实验结果证明,本文方法能很好地实现运动目标提取,并且节省了大量的调试参数的时间。但由于模型的局限性,在动态背景干扰很大时提取效果还不理想。因此在未来的工作中,将继续优化本文模型和算法,建立鲁棒性更强的优化模型并找到简洁、高效的奇异值分解算法,使之能更好地去除动态背景带来的剧烈干扰。
