多普勒效应在GPS诱骗识别领域的应用研究
2018-11-21王养柱
韩 震, 王养柱, 丁 典
(北京航空航天大学,北京 100089)
0 引言
GPS定位定速的精度高,因此被广泛应用在组合导航中。但近年来,针对GPS进行诱骗的电子对抗手段得到了广泛的发展。相比于电磁干扰,GPS诱骗信号难以察觉,不影响GPS乃至组合导航设备的正常工作,但是却可以通过长时间的缓慢诱骗,使无人机偏离正常的航线,甚至沿敌方预设轨迹运行。伊朗曾通过GPS诱骗的手段,成功捕获了一架美国生产的RQ-170“哨兵”无人侦察机;之后,美国德克萨斯大学的托德·汉弗莱斯团队也成功对无人机实施了欺骗,使无人机偏离到了指定的地点[1];KIM等分析了转发式诱骗信号对GPS接收机的影响[2]。
对此,国内有学者开始对GPS诱骗进行研究。诱骗的实质是使接收机捕获到虚假GPS信号从而生成错误的导航信息。目前,常见的诱骗方式包括产生式和转发式。其中,产生式诱骗是生成诱骗报文,将之与侦测所得的伪码进行调制后发送,具有很强的迷惑性,但其难度与成本很高;转发式诱骗则是将卫星信号延时后转发出去。戴文博等阐述了一种无人机欺骗诱导模型,给出了偏移速率的计算方法,理论上证实了将无人机诱骗至特定点的可能性[3];王海洋等验证了转发式诱骗以及生成式诱骗均能够成功地干扰GPS接收机[4];闫占杰等提出了一种便于实现的GPS诱骗式干扰源部署方法[5]。
与此同时,国内外学者也开始对GPS诱骗识别技术进行研究。GPS诱骗识别技术通常从信号发射端和接收端两个方面入手。发射端通过改善发射信号的鲁棒性来实现反诱骗的目的,接收端通常通过信号的频率、功率、到达角等数据来检测诱骗[6]。根据数据处理阶段的不同,诱骗识别技术又可以分为3大方面:信号体制、终端技术和外部辅助[7],每一方面都有相应的诱骗识别方法。其中,外部辅助方面通常由SINS,ADS等系统提供辅助数据。目前常见的识别算法有卡方检验法[8]、基于多旋翼模型的状态估计法[9]以及神经网络法[10]。陈碧等理论分析了诱骗终端需要使产生的码相位、多普勒频移、载波相位等参数与真实信号对齐[11]。
由于GPS误差的影响,卡方检验法以及神经网络法对GPS诱骗信号的识别效果较差,存在较大的漏检率以及误判率;而固定翼飞行器工况的复杂性,使得利用多旋翼模型状态估计进行判别的识别算法无法满足其诱骗识别的精度要求。
因此,本文从多普勒效应入手,分析了GPS诱骗装置应如何分布,如何补偿多普勒频移,同时也提出了一种在飞行器主动机动的情况下,可用来根据多普勒频移的变化情况来判断GPS接收机是否被诱骗的算法。
1 GPS诱骗中的多普勒效应
1.1 多普勒效应及频移
多普勒效应是指:波源与接收端存在相对运动时,接收端接收到的信号波长不再等于波源发射信号波长,而这个差值就是多普勒频移。多普勒频移算式为
(1)

GPS卫星和GPS接收机之间存在着相对运动,大部分情况下,多普勒频移不为零。而对于GPS诱骗装置而言,由于几何分布以及相对运动速度的不同,诱骗装置和接收机之间的多普勒频移是不等于卫星与接收机之间的频移的。
假设GPS卫星、GPS诱骗装置、GPS接收机、诱骗后的几何分布分别如图1所示。

图1 几何分布示意图Fig.1 Geometric distribution
图1中:GPS卫星位置为xs;GPS诱骗装置位置为xc;GPS接收机位置为x,速度为u;诱骗后的位置为x′,速度为u′。
这里假设由GPS卫星速度和GPS诱骗装置速度所引起的多普勒频移已经被补偿。
GPS接收机接收到的实际多普勒频移为
(2)
式中,Δf是诱骗开始时需要补偿的多普勒频移。
根据解算结果计算出的计算多普勒频移为
(3)
在诱骗开始时刻,有f=fR,则可得到初始频移补偿为
(4)
当GPS接收机载体进行机动,其位置增量为Δx,速度增量为Δu时,实际多普勒频移为
(5)
计算多普勒频移为
(6)
一般情况下,位置增量远小于接收机与卫星或者诱骗装置之间的距离,因此式(5)、式(6)中等式右侧的第二项、第四项均可以忽略,由此可得
(7)
根据式(7),便可分析诱骗装置几何分布以及诱骗装置补偿周期对频移的影响。
1.2 诱骗装置几何分布对频移的影响
令Δf保持初始值不变,即不再更新多普勒频移补偿量,则式(7)可简化为
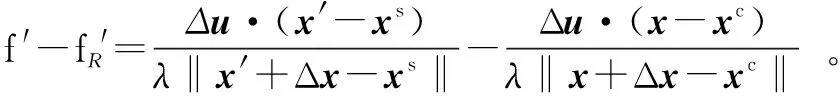
由此可知,当诱骗位置与卫星之间的单位位置矢量I′s,不同于接收机与诱骗装置之间的单位位置矢量Ic时,经过补偿、机动前相同的两个多普勒频移再次出现差值,且该差值与机动后速度的变化情况、位置矢量I′s与Ic之间的差异有关。
在诱骗开始的短时间内,诱骗位置与接收机位置之间的距离远小于卫星或诱骗装置和接收机之间的距离,因此,式(8)可简化为
(9)
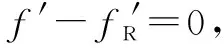
1.3 诱骗装置补偿周期对频移的影响
对于诱骗装置而言,若想实现多普勒频移的补偿,则需要实时获取诱骗目标的位置和速度,以此来计算出实际多普勒频移,并与计算多普勒频移进行比较,从而得到多普勒频移补偿量。对搭载组合导航系统的诱骗目标而言,计算多普勒频移的更新周期最短可为惯导系统的更新周期,因此,若诱骗装置能在惯导更新周期内计算出多普勒频移补偿量,并通过硬件设备完成对诱骗信号的补偿,则可及时对由位置产生的频移偏差进行补偿。若无法完成补偿,则机动后的某个时刻,可能会出现一个较大的多普勒频移偏差。
1.4 基于统计方法的诱骗识别算法
由于在诱骗发生阶段以及诱骗目标机动阶段,多普勒频移会出现偏差,因此可以利用残差检验的思想,来判断GPS接收机是否被诱骗。
一般情况下,多普勒频移偏差主要受白噪声、大气层延时等误差源的影响,根据中心极限定理,可认为多普勒频移偏差符合均值不为零的正态分布。因此,可以通过大样本来拟合出该分布的均值和方差,根据拉依达准则判断数据是否正常,从而判断GPS是否被诱骗。计算流程如下
a=sum(D)/N
δ=sqrt(sum((D-a)2)/N)
(10)
式中:N是选用的大样本的个数;D是样本值。多普勒频移的偏差的增量应在区间[a-3δ,a+3δ]。根据均值和方差的定义,可以求出两者在该样本下的近似数值a和δ,对于下一时刻的新样本数值,判断其是否在[a-3δ,a+3δ]内,若在,则认为GPS未被诱骗;反之,则认为GPS被诱骗。
2 仿真结果
在纬度方向上,轨迹发生器生成的轨迹以及诱骗后的轨迹如图2所示。

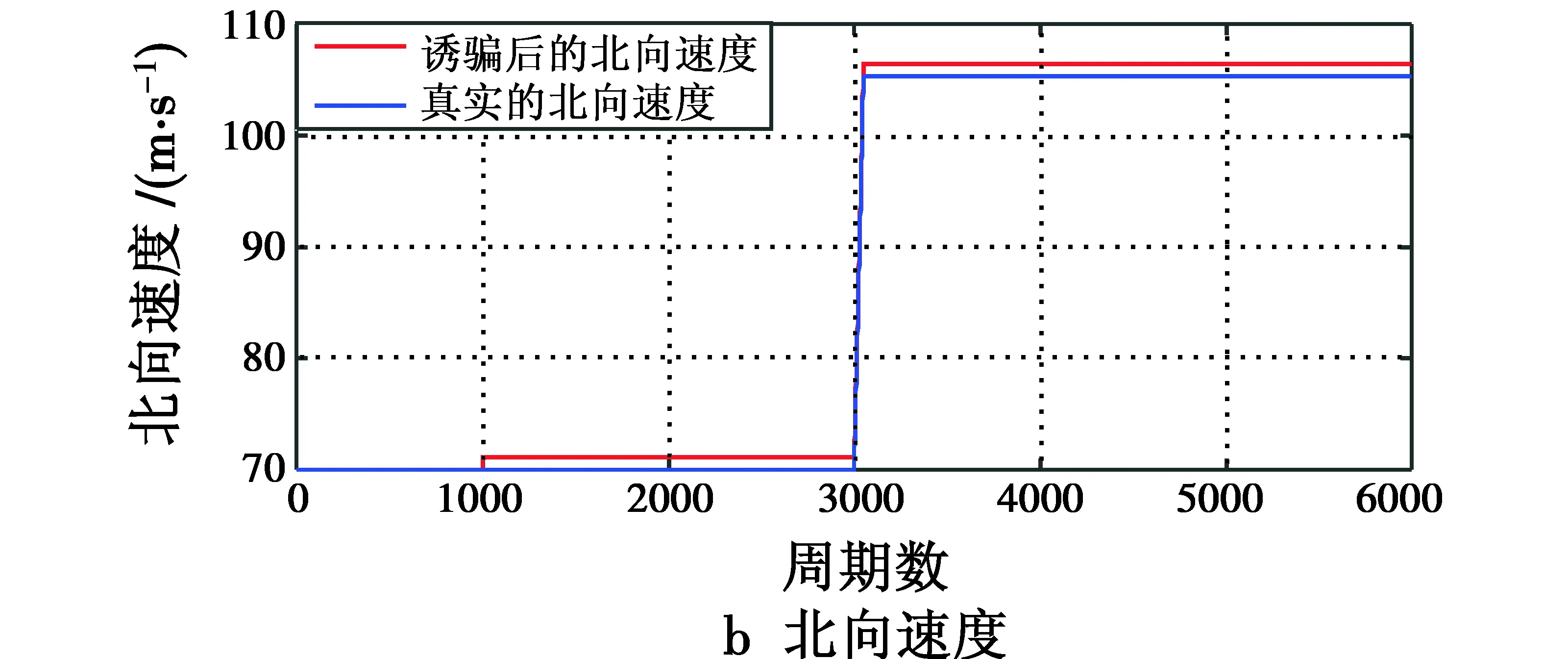
图2 纬度方向的轨迹Fig.2 Trajectory in the direction of the latitude
现考虑几何分布和补偿周期对多普勒频移的影响。仿真分3种情况:情况1,诱骗装置位于卫星和接收机的位置矢量上,补偿周期分别为0.2 s和0.5 s;情况2,诱骗装置仅在纬度方向偏离连线50 km(经度方向偏离造成的结果相似),补偿周期分别为0.2 s和0.5 s;情况3,诱骗装置仅在纬度方向偏离连线100 km(经度方向偏离造成的结果相似),补偿周期分别为0.2 s和0.5 s。仿真结果如图3~图5所示。

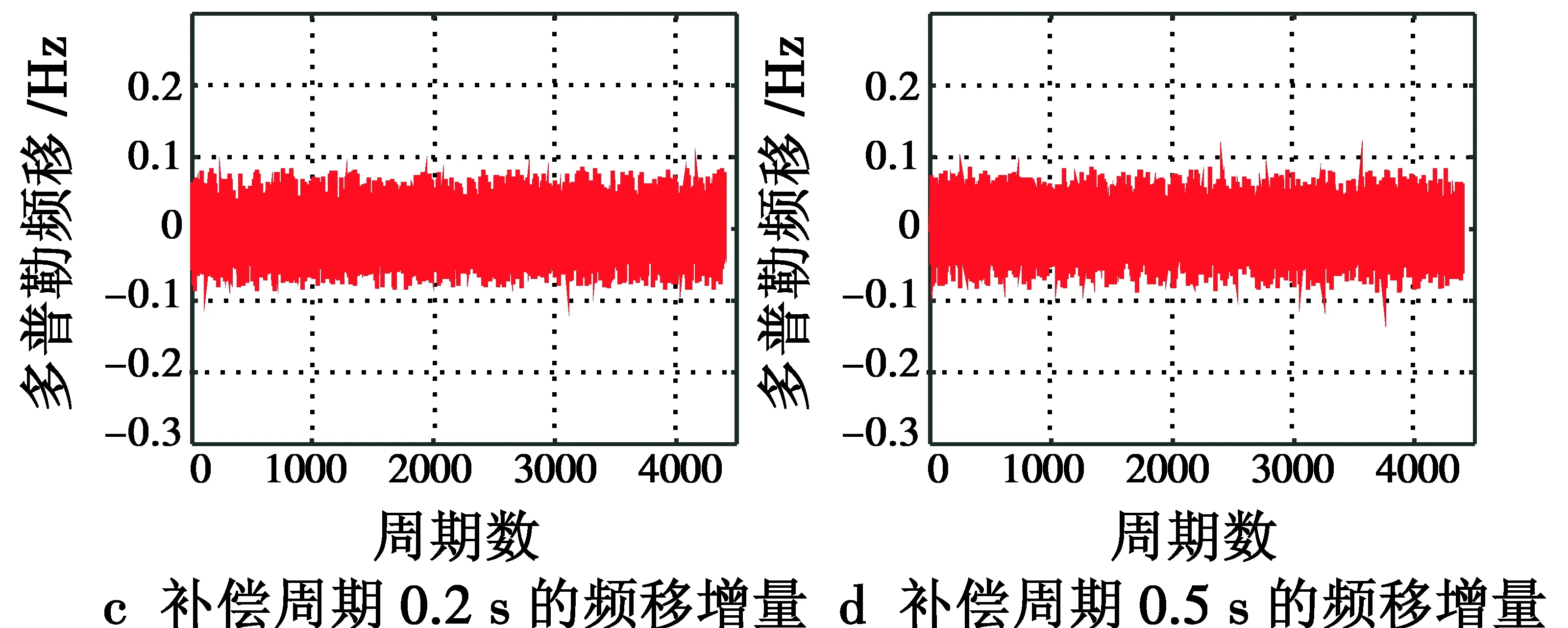
图3 情况1仿真结果Fig.3 Simulation result of Case 1
由图3可知,当诱骗装置位于卫星和接收机的位置矢量上时,机动过程不影响多普勒频移的偏差,换言之,诱骗装置仅需在诱骗起始时根据需要的诱骗速度对多普勒频移进行补偿即可。频移增量表示多普勒偏差前后时刻的差值,图3中仅取150~600 s这个区间内的数据,由图可知,诱骗装置的补偿周期不会对多普勒频移增量产生影响。
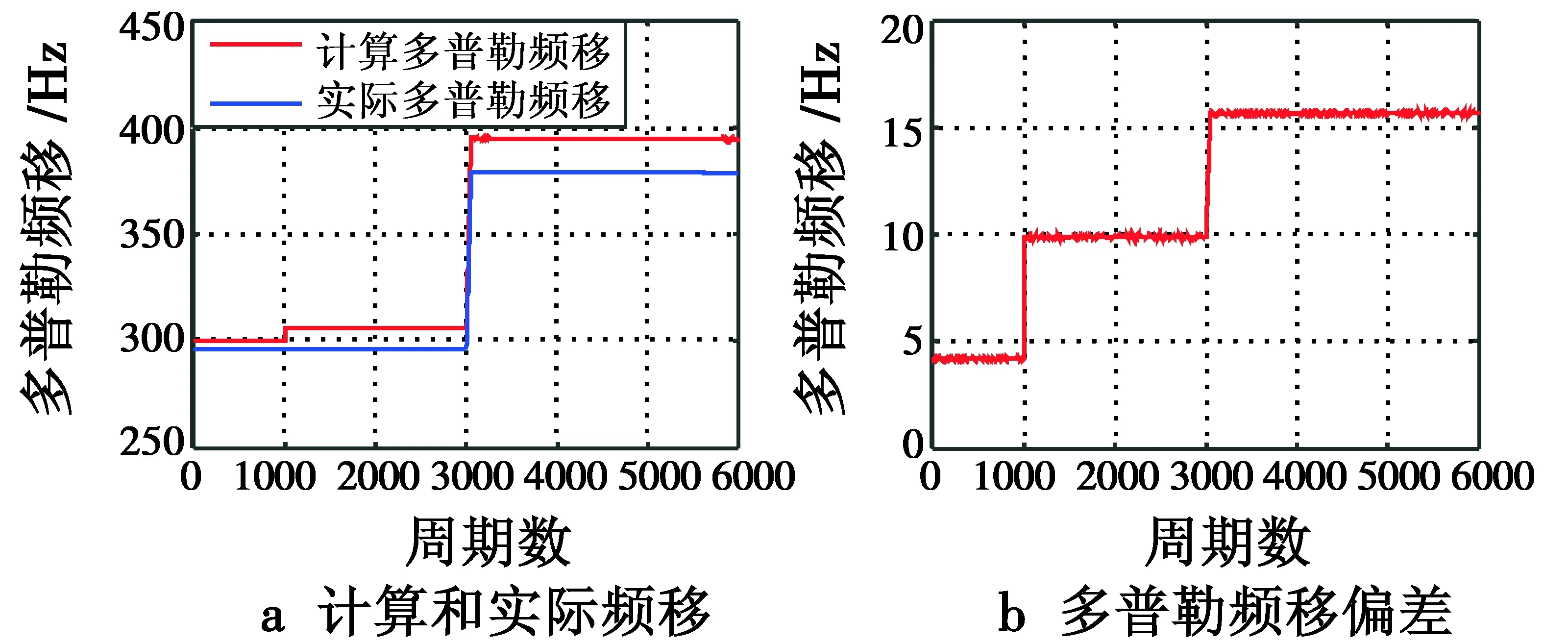
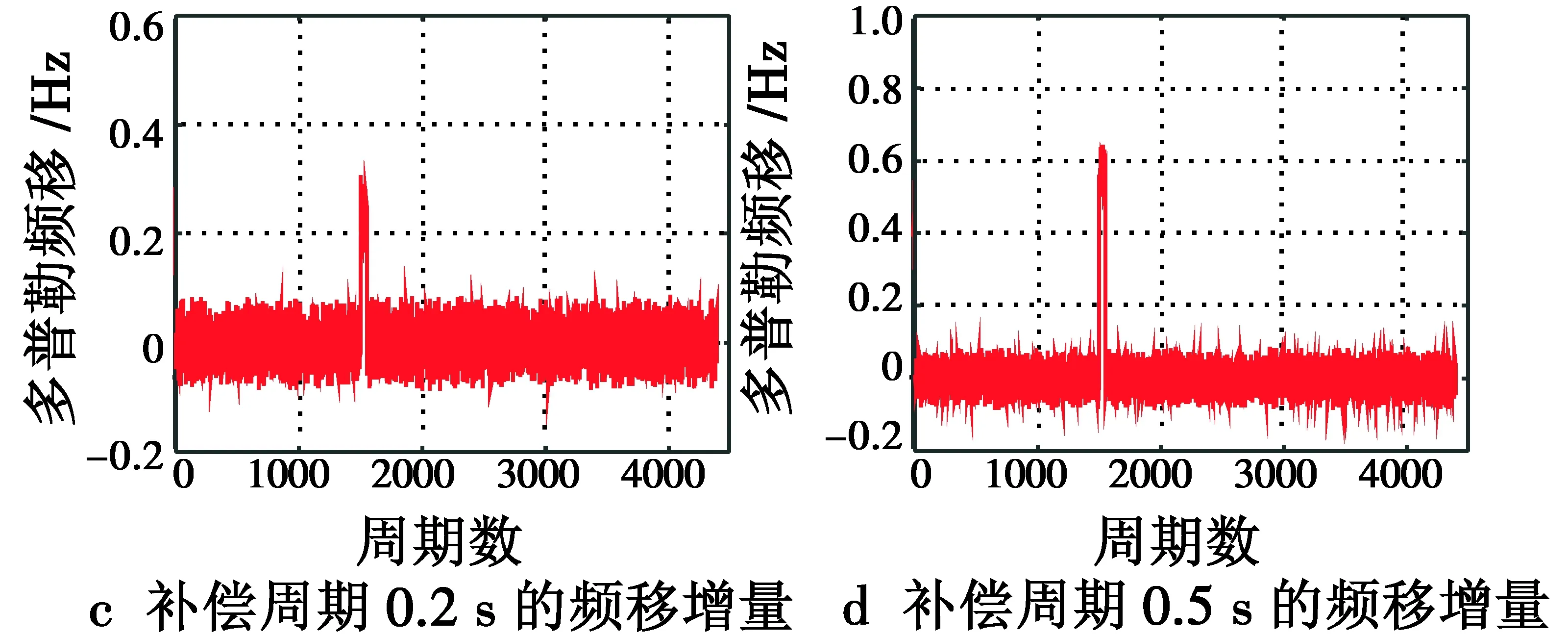
图4 情况2仿真结果Fig.4 Simulation result of Case 2
由图4可知,当诱骗装置在纬度方向偏离卫星和接收机的位置矢量为50 km时,机动过程会使多普勒频移偏差产生突变,与此同时,当补偿周期为0.2 s时,可见前后时刻的偏差会在产生机动的时刻发生突变;当补偿周期为0.5 s时,该突变的幅值明显增大。由此可知,当频移补偿周期大于识别算法周期时,多普勒频移无法同步,且两周期相差越大,多普勒频移的偏差也就越大。可通过对多普勒频移的偏差或频移增量进行实时监测,来判断GPS接收端是否受到诱骗。
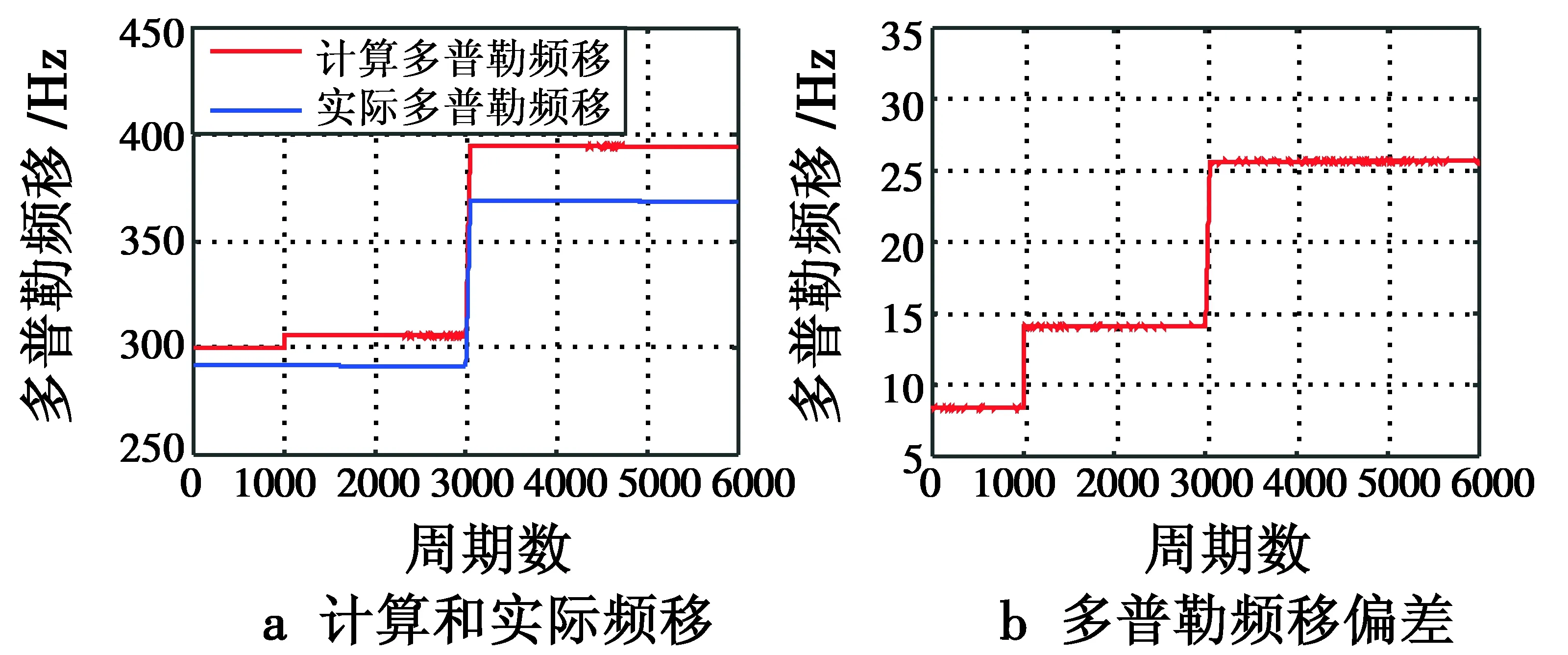

图5 情况3仿真结果Fig.5 Simulation result of Case 3
由图5可知,当诱骗装置在纬度方向偏离卫星和接收机的位置矢量为100 km时,仿真结果与图4结果具有相同的性质,但频移相关数据的幅值均有所增大,更有利于对GPS是否被诱骗进行识别。
针对在纬度方向偏离50 km的情况进行诱骗识别,分别采用200个和500个样本,从150 s处开始,分别对0.2 s和0.5 s这两个周期对应的频移增量进行识别,识别结果如图6所示。

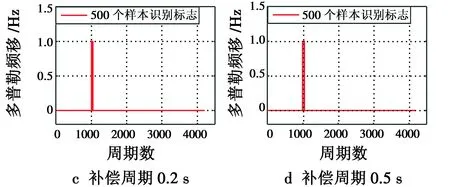
图6 诱骗识别结果Fig.6 Spoofing recognition results
由图6可知,200个和500个样本对应的识别算法均能够根据多普勒频移偏差成功地识别出GPS是否受到诱骗,其中,500个样本的识别算法虽然时间复杂度较大,但识别结果的准确率更高,因误判带来的跳变更少。
3 结论
诱骗装置的补偿周期若小于飞行器导航系统的更新周期,即诱骗装置在诱骗目标解算出实际多普勒频移和计算多普勒频移前,完成了对多普勒频移的补偿更新,则无论诱骗装置与诱骗目标的相对几何分布如何,通过机动均无法对诱骗进行识别;若补偿周期大于更新周期,能否识别诱骗则取决于相对几何分布。
若诱骗装置与诱骗目标的位置矢量平行于卫星与诱骗目标的位置矢量,则机动无法带来多普勒频移偏差,也就无法识别诱骗;当两位置矢量存在偏差时,飞行器机动则会带来多普勒频移偏差,该偏差可用来判断GPS是否受到了诱骗。
综上可知,位置矢量的偏差决定了多普勒频移偏差的有无与大小,补偿周期的大小则决定了能否在诱骗被发现前及时对多普勒频移进行补偿。
