基于诱骗策略的无人机协同航迹规划
2018-11-21朱杰,鲁艺
朱 杰, 鲁 艺
(空军工程大学,西安 710038)
0 引言
航迹规划最基本的要求是在保证无人机可以完成预定任务的基础上,综合油耗、飞行时间和威胁分布态势等因素规划出最优航迹[1]。现代战争中,威胁联网[2-3]凭借信息融合共享的优势,能够对入侵目标高效感知并快速调整防御态势,极大程度上增大了无人机的突防难度。现有航迹规划研究主要集中在新型算法的应用和改进方面,如微分进化算法[4]、蚁狮优化算法[5]和布谷鸟搜索算法[6]等,但随着地面防空武器性能的提升和部署密集度的增大,特别是威胁联网对防御态势的影响,仅依靠优化算法并通过函数寻优获得可行路径的航迹规划,实用意义越来越小。
“任务机+诱饵机”的协同作战方法,能够利用诱饵机介入威胁探测网的方式,在敌方探测网信息系统中形成入侵假象,使敌方调整其战略部署,从而为任务机突防提供机会,这种方法往往能达到更好的作战效果。在文献[7-8]中,提出了利用假目标无人机,通过电子欺骗干扰的方式掩护战斗机完成作战任务,但由于无人机为保证干扰效果,需要尽量将干扰方向指向探测威胁,容易被敌方识别,难以达到理想的效果;文献[9]提出了利用多机协同对组网探测进行欺骗干扰的策略,提高了干扰的效果,但同时也增加了干扰系统的复杂性和不稳定性;文献[10]中,分析了无人机作为电子诱饵实施欺骗干扰的优势,肯定了利用无人机进行战术诱骗的作战价值。纵观现有文献,均没有深入分析进行诱骗策略下的协同作战对于威胁联网环境中作战效果的影响。
针对上述问题,通过研究诱饵机运动策略对于联网威胁的影响,提出了无人机协同作战模型,并建立了诱饵机与火力威胁的相对运动数学模型。其次,考虑到火力威胁运动对于任务机规划航迹的影响,提出了任务机航迹规划的原则并改进了代价函数,规划出了合理航迹。同时,该诱骗策略也适用于有人机与无人机间的协同作战[11]。
1 问题描述
1.1 无人机协同作战原理

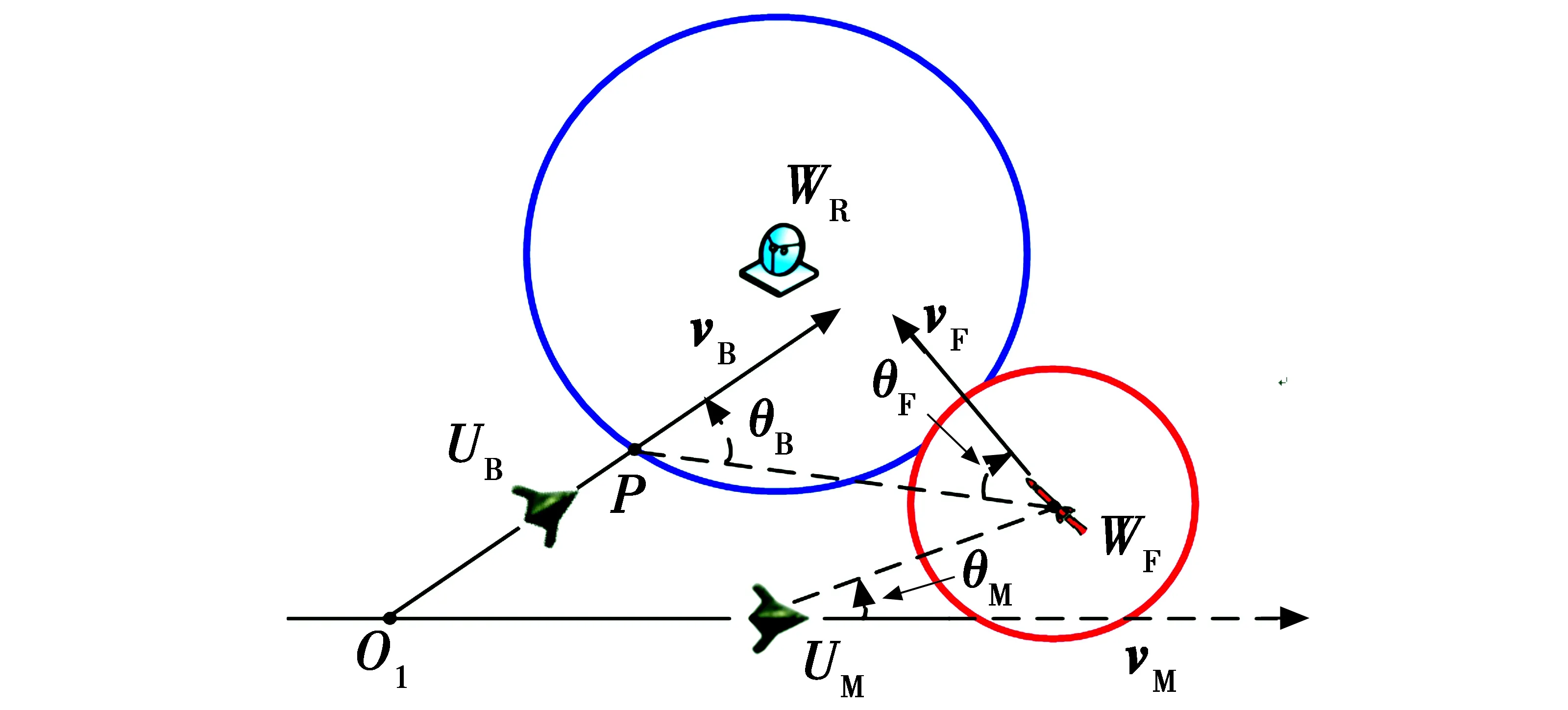
图1 无人机协同作战态势图Fig.1 The situational figure of multi-UAV cooperative operation
1.2 协同作战实现流程
无人机协同作战的具体运行流程如图2所示。战场态势信息获取是整个作战行动的前提保证,主要包括敌方威胁源位置、地形、天气等各类在航迹规划中所需考虑的因素,战场态势获取直接影响战术决策实施的准确性。战术决策是作战行动的核心,基于获取的敌方部署情况,通过预测火力威胁及己方参数,调控诱饵机和任务机的运动轨迹,以达到预期目的。诱饵机的运动直接决定火力威胁的机动策略,而任务机通过对火力威胁运动情况的判读,评估火力威胁对自身的威胁程度,从而调整自己的运动轨迹。
进行战术决策前需要准确获取各类信息,为无人机协同提供决策依据。在战术实施阶段,首先通过调整诱饵机的运动参数vB和θB,对火力威胁实施诱骗并实时获取火力威胁的运动参数vF和θF。其次,分析任务机与火力威胁的位置关系,结合火力威胁的运动参数vF和θF,评估火力威胁的威胁程度并调整vM和θM使得任务机顺利突防。战术决策流程如图3所示。
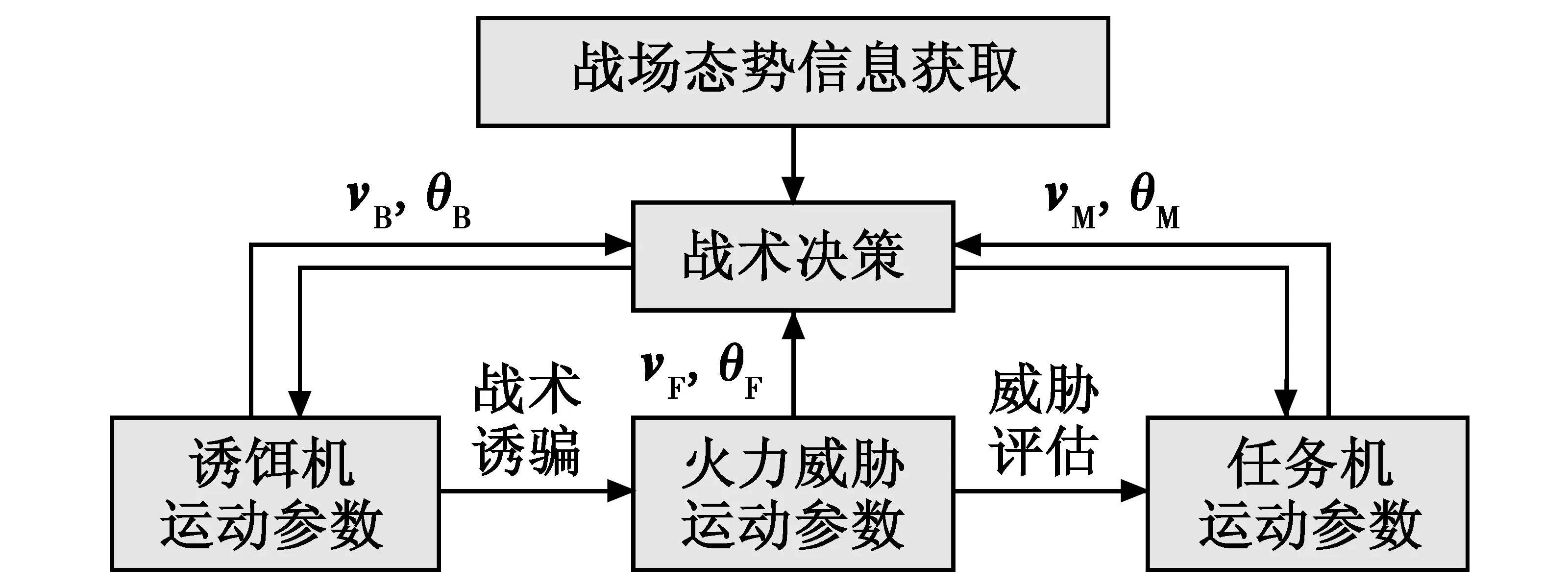
图2 协同作战流程Fig.2 The process of UAV cooperative operation
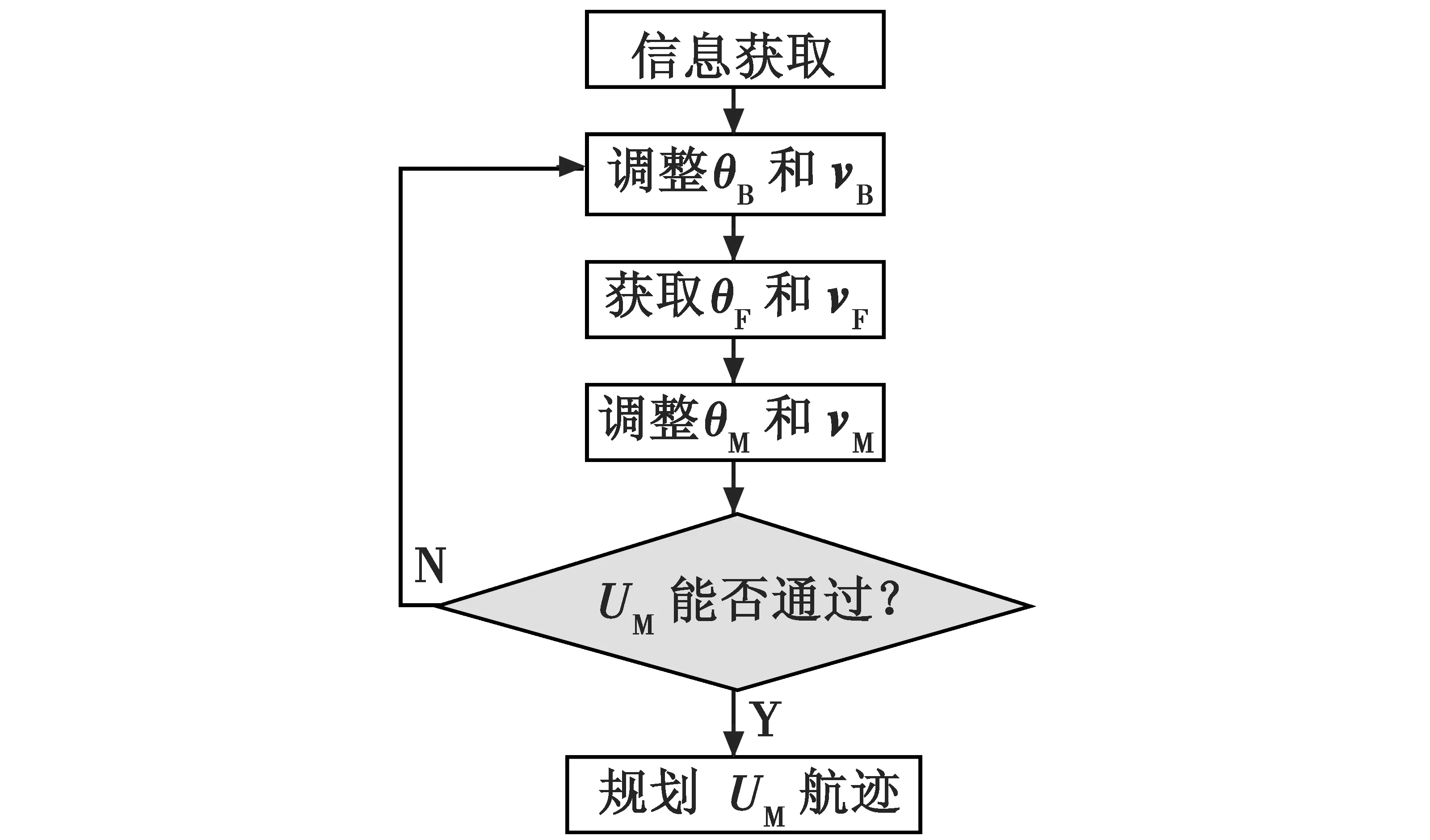
图3 战术决策流程Fig.3 The process of tactical decision-making
2 数学模型
为了精确分析战术诱骗对航迹规划的影响,首先必须建立诱饵机与火力威胁的相对运动数学模型,以确定两者的运动关系。当诱饵机进入敌方探测威胁覆盖区域时,探测威胁会将诱饵机信息发送给火力威胁,火力威胁将根据所给信息进行机动,拦截诱饵机。假设某一个时刻,诱饵机位于G点,火力威胁位于W点。连线GW称为目标瞄准线,选取Ax为参考线,它可以任意选取且选取位置不同不会影响模型的运动分析。具体模型如图4所示。
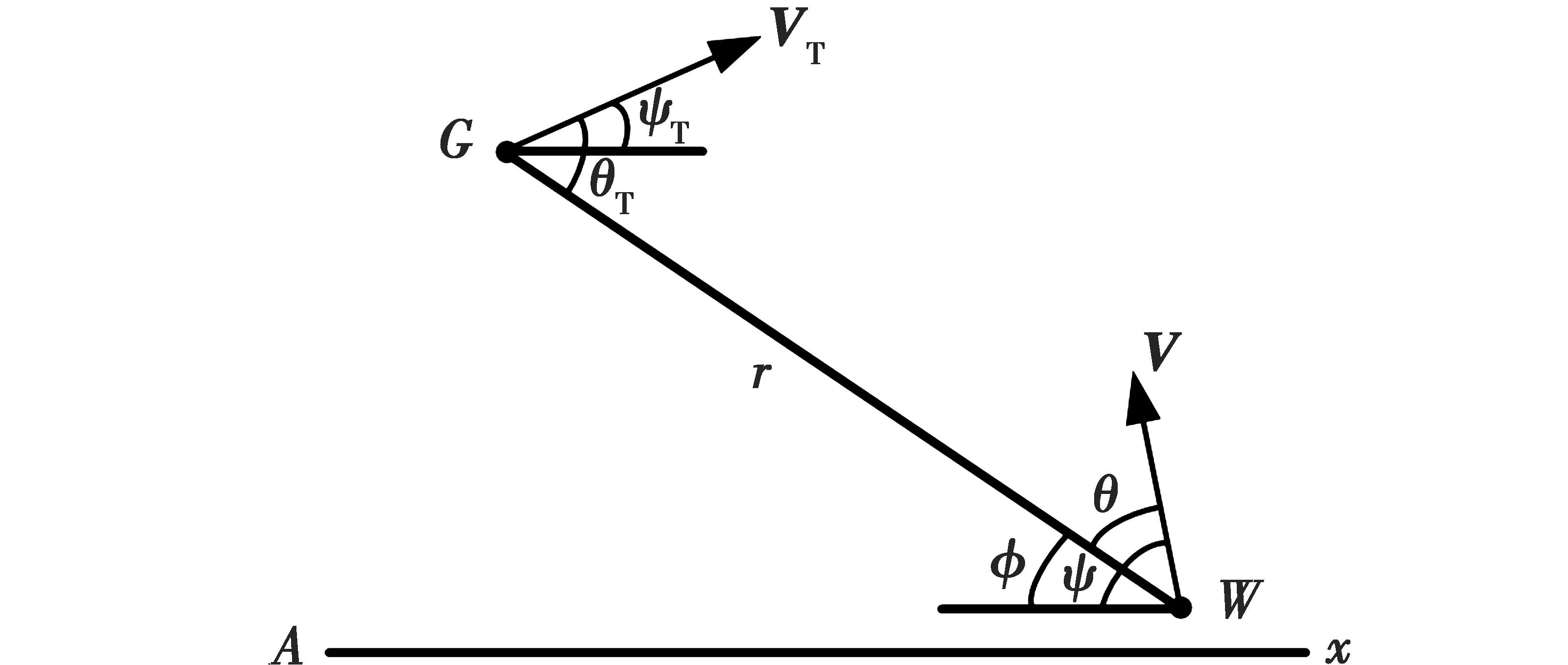
图4 相对运动模型Fig.4 Relative motion model
图4中,V,VT分别为火力威胁和诱饵机的速度矢量;θ,θT为速度矢量与目标瞄准线间的夹角;ψ,ψT为速度矢量与参考线间的夹角;φ为目标瞄准线与参考线间的夹角,r为诱饵机与火力威胁的相对距离。角度旋转逆时针方向为正,则由此可得描述相对距离r和角φ变化率的方程为
(1)
(2)
同时考虑到角度关系和追踪关系可得如下方程
φ=ψ-θ
>,
(3)
φ=θT-ψT
>。
(4)
ε=0为火力威胁追踪诱饵机的运动关系控制方程,一般可表示为
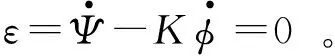
(5)
敌方通过控制参数K的大小,确定追击诱饵机的运动关系,同时也决定追击目标的难易程度。将式(3)求导并代入式(5)可得
(6)
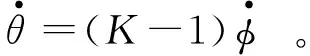
(7)
由式(6)、式(7)可得:
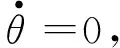
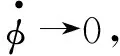
(8)
3 基于遗传算法的任务机航迹规划
遗传算法是模拟自然选择和遗传进化过程的计算模型,是一种通过模拟自然进化过程寻求最优解的方法。由于遗传算法具有全局搜索能力强、不受函数约束条件限制并具有并行搜索特征,而且优化计算不依赖于梯度信息,不要求目标函数连续可导等优点,可广泛用于解决各类大规模、非线性组合优化问题。
3.1 航迹坐标编码
在遗传算法中,航迹坐标的编码方式在一定程度上会影响算法的计算性能。本文在适当约束下,简化了航迹的编码方法,如图5所示,建立直角坐标系xoy。在坐标系中,将航迹起点到终点的横坐标按固定步长均分为N段,长度为l。由于不同航迹相应步长处的横坐标是相同的,而区别仅在于其纵坐标不同,因此,利用遗传算法仅将航迹点的纵坐标作为基因位进行编码。考虑到无人机自身性能约束,通过调整步长和转弯角,使得l≥lmin,且Δθi≤θmax。
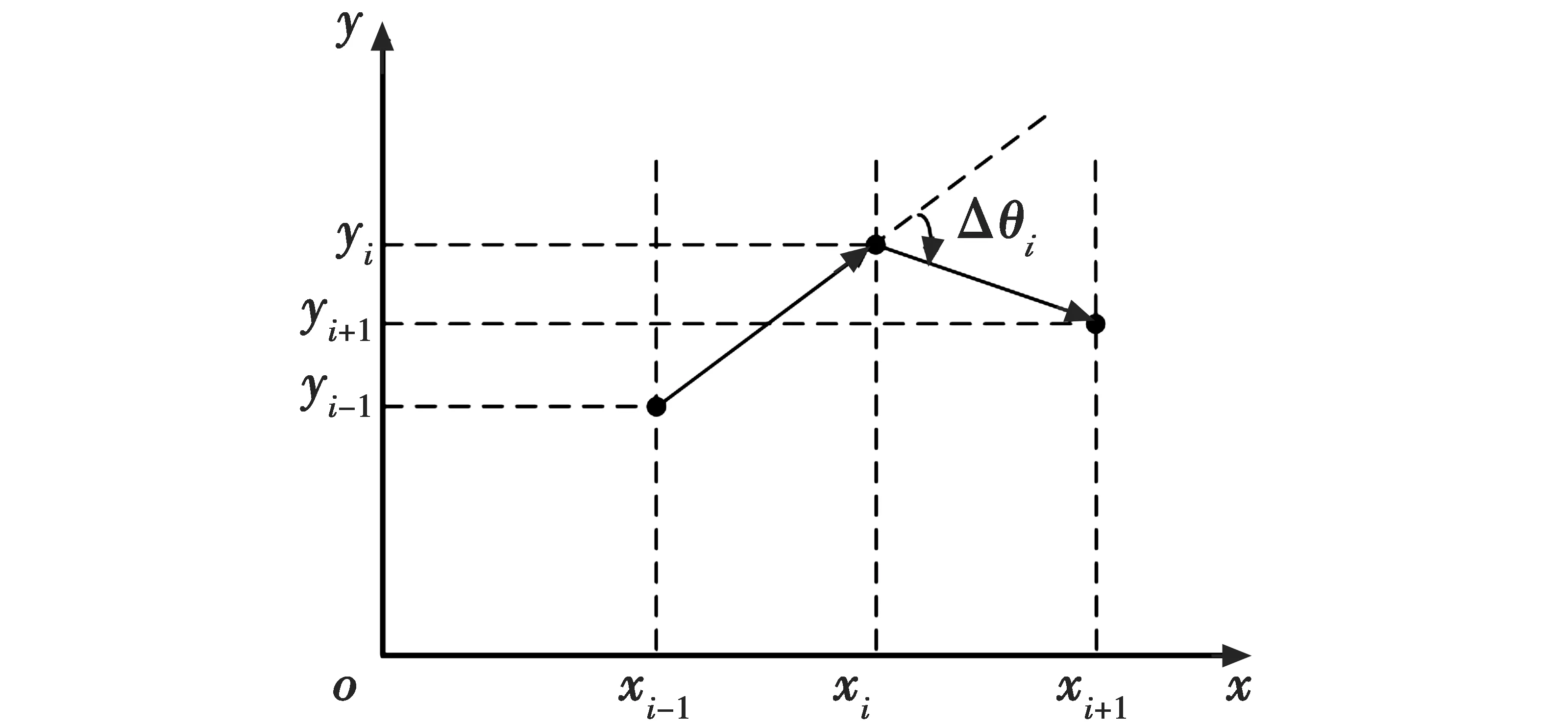
图5 航迹编码示意图Fig.5 Path coding figure
3.2 适应度函数确定
任务机在飞行过程中,一方面必须实时掌握火力威胁的位置信息,首先保证不会进入火力覆盖范围内,其次考虑整体航迹的代价最小;另一方面,任务机是否能够顺利穿越火力威胁区域,不仅由规划出的航迹决定,其飞行速度也会影响任务的完成。
由于火力威胁的位置是不断变化的,因此任务机必须保证在任意时刻都不会进入火力覆盖范围。设在t时刻任务机坐标为(x(t),y(t)),火力威胁坐标为(xW(t),yW(t)),则任务机航迹代价为
(9)
式中:JW为威胁代价;JL为航程代价;w为代价权值,取值范围是0~1,威胁及航程代价采用文献[13]中提出的计算方法;Kp为开关函数,计算方法为
(10)
(11)
式中:R为t时刻任务机和火力威胁之间的距离;Rp为火力威胁的覆盖半径;Vmin为任务机可以穿越威胁区域的最小速度;Vmax为任务机的最大飞行速度。开关函数判断规划航迹的可行性,保证任务机能够顺利突防。若Xi表示第i条航迹,则航迹的适应度函数为
Fitness(Xi)=1/J(Xi)>。
(12)
4 仿真分析
4.1 战术诱骗模型仿真分析
进行战术诱骗的目的是为了诱导火力威胁离开原来部署地点,为任务机突防提供机会,评价指标为火力威胁机动后距离原部署地的距离和火力威胁拦截诱饵机所需时间,分别用l和t表示。诱饵机入侵敌方探测网的角度和速度会使评价指标发生变动,而进行战术诱骗的目的就是通过调整诱饵机的运动参数以获得利于任务机顺利突防的最佳评价指标。
图6所示分别为两种K值下,速率比M取不同值时,诱饵机(目标)的偏离角度θB与火力威胁追击到诱饵机时间t的关系曲线。
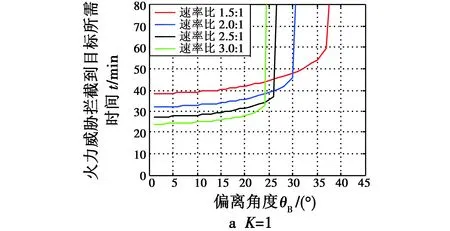
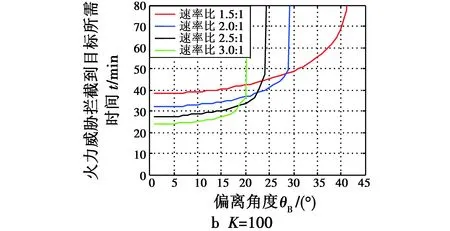
图6 不同K值时θB-t对比Fig.6 θB versus t at different K values
当K值一定时,从图6a中可以得出:1) 相同速率比情况下,目标飞行方向偏离火力威胁越远,火力威胁拦截目标所需时间越长;2) 相同偏离角度情况下,速率比越小,火力威胁拦截目标所需时间越长;3) 速率比越大,火力威胁拦截到目标的时间发生突变,即火力威胁能否拦截目标的临界值(偏离角度)越小。对比图6a、图6b可得:在相同速率比情况下,K值较小,速率比较大时,火力威胁能否拦截目标的临界值越大;反之,K值较大,速率比较小时,火力威胁能否拦截目标的临界值也越大。
图7所示分别为两种K值下,速率比M取不同值时,诱饵机(目标)偏离角度θB与火力威胁离初始位置距离l的关系曲线。
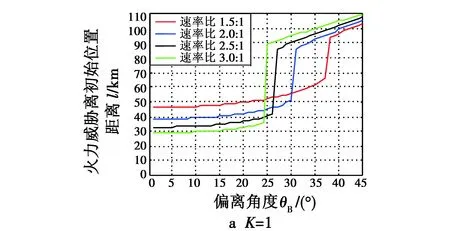
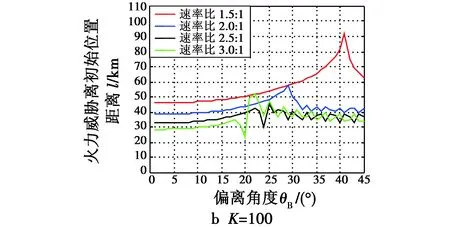
图7 不同K值时θB-l对比Fig.7 θB versus l at different K values
从图7中可以得出,偏离角度变化时,火力威胁离初始位置距离的变化趋势与火力威胁拦截目标所需时间的变化趋势相同,但K=100,速率比一定,当偏离角度超过火力威胁能够拦截到目标的角度时,火力威胁将不能再继续追击目标。
综上所述,诱饵机诱骗需要满足在保证火力威胁能够成功拦截的情况下,以较低的速率和较大的偏离角度进入敌方探测威胁覆盖区域。
4.2 无人机协同航迹规划
选取威胁区域为500 km×500 km的航迹规划空间,该空间内有探测和火力两种类型的威胁,其中探测威胁有两种威胁权重,参数设置如表1所示。

表1 威胁参数

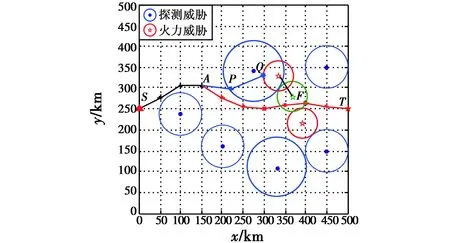
图8 协同航迹规划Fig.8 Cooperative path planning

5 总结
本文在建立诱饵机与火力威胁的相对运动数学模型基础上,通过改变诱饵机飞行速度和方向,分析了诱饵机运动参数改变对火力威胁运动距离和拦截时间的影响,提出了诱饵机与任务机的协同原则。所建立的数学模型虽然不能完全模拟实际战场环境,但通过调节数学模型参数可以得到诱骗过程中敌我的整体运动态势,为决策者提供了相对合理的参考。另一方面,利用无人机进行协同战术诱骗以达到突防目的的方法,为应对威胁联网下的无人机航迹规划提供了新的思路。但由于实战环境复杂多变及无人机战术协同的实时性要求,航迹的规划应具备较强的局部调整能力,这还需进一步研究完善。仿真结果表明,利用战术上的诱骗可以实现无人机在威胁联网环境下的突防,这证明了合理的战术运用也能获得较好的作战效果。
