对数正态分布条件下某光耦步进加速退化试验优化设计
2018-11-21张烜工穆希辉
张烜工, 穆希辉, 冯 静
(1.陆军工程大学石家庄校区,石家庄 050000; 2.湖南银杏数据科技有限公司,长沙 410100)
0 引言
加速退化试验的设计与优化是统计分析的逆问题,研究在一定的约束条件下,如何进行加速退化试验以获得可靠度和寿命的准确估计。当前关于加速试验优化设计有着诸多研究,总体来说有两类方法:解析法和仿真法。根据查阅到的文献来看,解析法和仿真法最早均由NELSON提出[1-2],仿真法在国内最早由汪亚顺系统梳理总结并应用[3]。TSENG和YU提出了退化试验终止准则,使数据统计结果更准确[4];WU和CHANG在费用约束条件下以p阶分位寿命的均方误 差最小为目标,建立退化率服从指数分布的退化试验 优化设计方法[5];YU和TSENG以p阶分位寿命方差最小为目标,在费用约束条件下,分别对退化率服从对数正态分布和倒数Weibull分布的退化试验进行了优化设计研究,得到了最优的样本数、监测频率和试验监测次数[6-7];王浩伟等研究了基于加速因子不变原则的加速退化试验优化设计方法[8]。以上都是通过解析的方法对加速退化试验进行优化设计。由于解析方法的推导过程比较复杂,并且在诸多场合下难以求出或者没有解析解,进而导致获取最优方案十分困难。鉴于此,目前的主流研究方向是选择仿真基的方法进行优化设计。汪亚顺和张春华[9]给出了仿真基混合效应模型加速退化试验方案优化设计的一般流程;潘刚[10]在给定样本量的前提下使用蒙特卡罗仿真方法研究了小样本条件下步降加速退化试验优化设计;谭源源[11]研究了在竞争失效条件下的仿真基加速退化试验优化方案;罗赓[12]则基于BP神经网络使用仿真基方法研究了在选定四应力水平下加速寿命试验的优化设计;葛蒸蒸[13]采用非参数统计分析的方法使用仿真基对应力水平以及各水平下样本分配进行了优化。但是仿真方法面临的主要问题在于指定退化轨迹模型形式,并且指定某些系数服从倒数Weibull分布,进而指定产品寿命分布服从Weibull分布,这对其来说是很大的掣肘。从理论上来说,仿真基的优化设计方法与解析法殊途同归,只不过仿真基的方法在于预先指定系数分布和寿命分布,避免了不存在解析解的困扰,同时设立解池,在其中挑选最优解,进而获取最优方案。基于此,结合实际的工程应用背景,本文使用改进的仿真基优化方法对光耦进行加速退化试验优化设计。
本文首先确定基于蒙特卡罗仿真的优化设计理论框架,再构建步进加速退化试验的统计分析模型,对步进退化数据进行折算,然后在建立极大似然函数的基础上,对现有的仿真基优化设计方法进行改进,最终建立优化设计的算法并对光耦的加速退化试验进行优化设计,得出最优的试验方案,同时也为寿命分布满足对数正态分布的产品加速试验设计提供参照依据。
1 基于蒙特卡罗仿真的优化设计理论框架
仿真基优化设计方法采用蒙特卡罗方法,其大致流程为仿真、统计分析和优化,对优化设计亦即统计分析的逆问题最终又转变为模拟试验数据的统计和分析,极大降低了优化设计的难度,其设计过程既可以简化又可以流程化实现。经过归纳总结,其理论框架如图1所示。
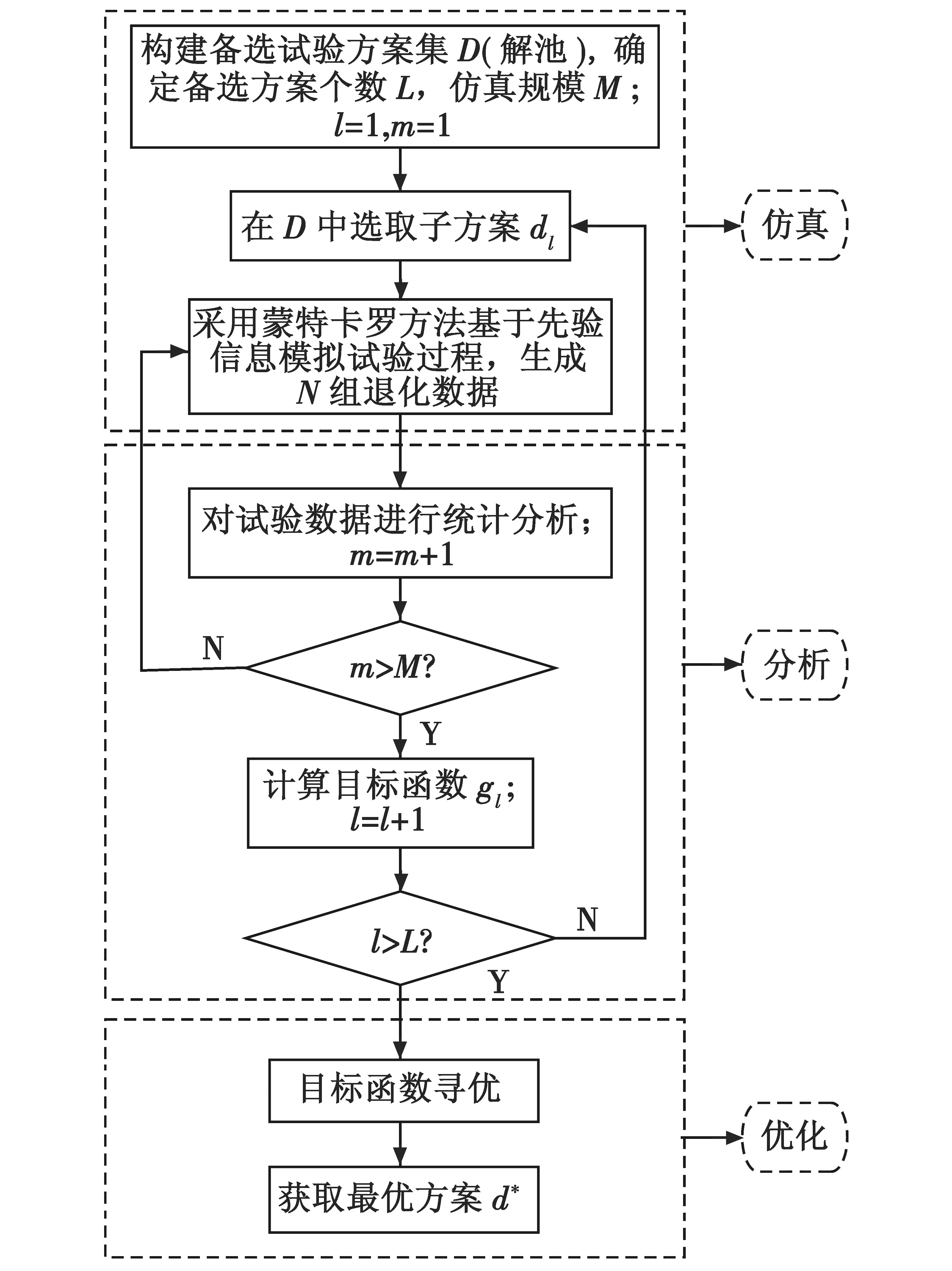
图1 基于蒙特卡罗仿真的优化设计理论框架Fig.1 The theoretical framework of optimal designbased on Monte-Carlo simulation
2 基于对数正态分布的步进退化加速试验的统计分析模型建立
2.1 混合效应模型和加速模型的基本假设
2.1.1 混合效应模型
根据文献[9],假设被测性能参数的退化轨迹可用混合效应模型描述如下,即
y(t)=β1tβ2+C
(1)
β1~LNμβ,σ2β>。
(2)
文献[9]中假设退化率β1服从倒数Weibull分布,而本文假设β1服从对数正态分布。上式中,β2和C是固定的。β2>0,认为β2与失效机理相关,因此是常数;C是被测性能参数的初值,简化起见,也令C为常数。
2.1.2 加速模型
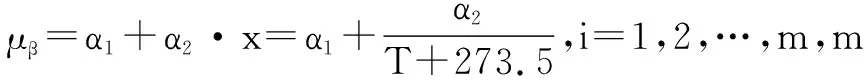
(3)
式中,D为被测性能参数的失效阈值。
2.2 步进加速退化试验的应力施加过程
步进加速退化试验应力施加过程如图2所示。

图2 步进加速退化试验应力施加过程Fig.2 Stressing process of step-up accelerated degradation test
以温度作为加速应力对光耦进行步进加速退化试验,共有m个应力水平。设正常的应力水平为S0,加速应力为S1,S2,…,Sm,S0 对于在步进加速试验中得到的退化数据,除了在S1下测得的数据为真实的退化数据外,其余应力水平下的测试数据均为累积退化性能数据。必须对数据进行折算,才能得到真实的退化数据。根据NELSON提出的累积损伤假定,结合前面给出的退化模型,利用被测性能参数的退化速率仅与当前应力水平有关而与前面经历的退化过程无关这个特性,其累积加速退化轨迹可描述为 (4) 式中:m是应力的个数;wi是在Si下的等效起始时间,由于在第一个应力下不存在等效起始时间,因此w1=0。所谓等效起始时间,就是指在应力Si下试验wi时间的退化量与截止到Si-1应力水平下产生的退化量相同的这段时间。根据之前的假定,式(4)可以表述为 (5) 式中,wi满足式(6)。 (6) 将式(6)变形,有 (7) 式中:w1=0;τ0=0。前文已述,退化率β1i服从对数正态分布,为了使后续的计算简便,设第j个样本在应力Si下的退化率为β1i=ξjexp(α1+α2·Si),其中,ξj~LN(0,σβ),j=1,2,…,n。式(7)是一个迭代式,使用起来并不方便,利用归纳法可以得到式(7)的最终表达式为 (8) 至此,结合式(5)和式(8),建立了光耦步进退化加速试验的统计分析模型。 1) 根据式(8),计算应力水平Si下的等效起始时间wi。 2) 由于ξj服从对数正态分布,对ξj~LN(0,σβ)进行n次抽样,获取n个ξ值。由β1i=ξjexp(α1+α2*Si),计算每个样本在不同应力下的伪退化率。 3) 计算应力的转换时刻τi=f*li和测试时刻k*f(i=1,2,…,m,k=1,2,…,K)。 4) 由εj i k~N(0,σε)抽样获得每个样本在每个应力下的各个测量点的测试误差εj i k。 无论是使用解析方法还是使用仿真基方法,极大似然函数的构建都是优化设计的根基。假定在应力Si下对第j个样本测量(li-li-1)次,不考虑初值的随机性,认为初值为一个常数。测试误差为εj i k,其相互独立且都服从标准正态分布,即εj i k~N(0,σε)。根据极大似然估计理论[15],第j个样品测试数据的极大似然函数为 (9) 当共有n个样本进行试验时,其对数似然函数为 (10) 式中,K为测试的总次数。由图2可知,τi为应力从Si转到Si+1的时刻。前文已述,τi和每个应力下最后一次测量的时刻相对应,即τi=tli。wi是在Si下的等效起始时间,计算方法为式(8)。 本文研究的目的在于评定长储后光耦的寿命,亦即其可靠度,因此优化目标为可靠度的估计精度。为了获得光耦在长储条件下贮存可靠度的精确估计,本文以正常应力条件下t时刻的光耦贮存可靠度估计值的渐进方差最小为目标,对步进加速方案进行优化。而正常应力条件下t时刻的光耦贮存可靠度估计值的渐进方差可以表示为 Var[R0(t)]=HF-1HT (11) 式中:H是R0(t)分别对C,α1,α2,β2,σε和σβ的一阶偏导的1×6矩阵,而R0(t)=1-Fe(t),故R0(t)是上述参数除σε外的函数,对上述参数求偏导后可以求得具体的解析表达式;F为Fisher信息阵,是式(8)对各项参数的负二阶偏导的期望。限于篇幅,这里不再给出F的表达式。 无论是解析方法还是仿真基方法的优化设计,都无法回避对F的求解。但是,经过计算,F里面的元素是无法求出解析解的,只能得出拟解析解。YU和TSENG通过解析方法研究了退化率服从对数正态分布时的退化试验优化设计情况[6];陈文华也采用解析方法对退化率服从对数正态分布时进行了加速寿命试验的优化设计[16],但是他们都是在恒定应力下进行的优化设计,不涉及数据折算,其对数似然函数自然与式(10)不同;汪亚顺等进行仿真基优化设计时,往往都是指定退化率服从倒数威布尔分布,进而指定寿命服从威布尔分布,因为威布尔分布条件下F中的元素是存在解析解的。但是本文通过之前的失效物理分析认为光耦由退化导致的失效服从对数正态分布,并不是威布尔分布。通过目前查阅的仿真基优化设计的文献来看,在步进应力条件下,绝大多数仿真基文献都是指定寿命服从威布尔分布,目前尚未查询到步进条件下指定寿命服从对数正态分布的仿真基文献。理论上来说,可以通过取近似值的办法来代替解析表达式中的拟解析解,但是即便如此,其二阶偏导的推导过程也非常复杂和繁琐,并不适合工程应用。这也是仿真基优化的文献中通常不指定步进应力条件下寿命服从对数正态分布的原因,渐进方差Var(R0(t))难以求出。 潘正强等指出,将渐进方差的大小作为衡量寿命指标估计优劣的准则是基于大样本理论的,指出在绝大多数场合下估计的极限分布为正态分布[17]。因此,光耦的可靠度R0(t)的极大似然估计值可以视为渐进服从均值为R0(t)、方差为Var(R0(t))的正态随机变量。基于这一理论,在不能或者难以求出Var(R0(t))的解析表达式的情况下,用Var(R0(t))的期望和标准离差来描述Var(R0(t))。显然,其期望越小,方案的精度就越高,其标准离差越小,则方案的稳健性越好。至此,将仿真基的优化设计方法进行了改进,不再计算渐进方差,而是计算渐进方差的期望和标准离差,解决了无法获得渐进方差解析解的问题。其期望和标准离差的计算式在下文中给出。 (12) 现利用改进的仿真基算法求取渐进方差的期望和标准离差,进而对光耦的步进加速退化试验进行优化设计。为了保证目标函数的精度,仿真规模M和抽样次数N均取1000。其具体步骤如下所述。 1) 设立解池,根据约束条件求出所有的测试次数分配。 2) 取出一组测试次数分配。 5) 计算可靠度估计值的伪方差,为 (13) (14) (15) 7) 重复步骤2)~6),直到解池中所有的解求出μV和σV,在点对合集中寻找使μV和σV最小的方案即为最优方案。 基于前面的理论推导,结合本文研究的实际背景,其具体参数设定如下:光耦的数量是固定的,即n=12;通过前期的摸底试验,温度应力设定为70 ℃,90 ℃以及110 ℃;固定测试频率f=8 次/h,当给定总的试验时间352 h后,总的测试次数44是固定的。因此各应力下测试的次数分配是要优化的方案。为了保证曲线拟合和外推的准确性,规定每个应力水平下测试次数不少于10次,并且满足li>li+1(i=1,2,3)。由于解池中共有15种方案,方案种类并不是很多,这里采用了全部计算出目标函数然后逐个比较寻优的方法。经过寻优发现μV和σV最小同时出现在(23,11,10)这个方案中。而对于传统试验方案来说,各个应力下的测试次数是均等分配的[18]。表1是测量次数均等分配的传统试验方案与优化设计方案的对比。 表1 传统试验方案与优化设计方案对比 由表1可以看出,优化设计方案无论是在精度还是在稳健性上都优于传统试验方案。如果从加速模型的角度分析,优化设计方案在低应力水平下分配的试验时间更长,测量的数据更多,亦即在低应力水平下获取了更多的退化信息,模型在外推时准确度更高。因此优化设计方案优于传统的试验设计方案。 本文对寿命服从对数正态分布条件下的仿真基加速退化试验优化设计进行了研究,推导了数据折算公式,进而建立对数正态分布条件下的步进数据统计分析模型,对现有的仿真基算法进行了改进,给出在对数正态条件下仿真基优化设计的一般算法。根据与传统试验方案对比,本文给出的优化方案精度和稳健性都更高。本文结合实际应用背景对各应力下的测试分配次数进行了优化,方法是通用的,也可以用于样本量以及应力分配的优化,补充和完善了现有仿真基优化的理论框架,为对数正态分布寿命的产品步进加速试验设计打下良好的工程应用基础。2.3 退化数据的折算
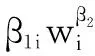
3 仿真基加速退化试验优化方法研究
3.1 仿真数据的获取
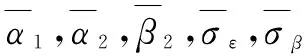
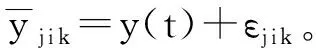
3.2 极大似然函数的建立
3.3 仿真基优化设计方法的改进
4 仿真基光耦步进加速退化试验优化设计算法
4.1 基于极大似然估计的R0(t)的Matlab理论求解
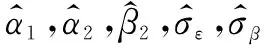
4.2 仿真基光耦步进加速退化试验的优化设计算法
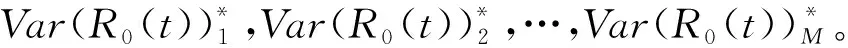
4.3 光耦步进试验优化设计与结果分析

5 结束语
